10.4: Colisiones

Consideremos ahora la situación en la que dos partículas chocan entre sí. Puede haber varios resultados de esta colisión, de los cuales estudiaremos dos:

• Las dos partículas chocan elásticamente, en esencia rebotando una de la otra.
• Las dos partículas se pegan entre sí, dando como resultado la producción de una sola partícula, o una sola partícula se rompe en dos partículas. Se trata de procesos inelásticos.

En ambos casos se conserva la energía y el impulso. Suponemos que las fuerzas que actúan entre las partículas son de corto alcance, de modo que excepto en el instante de colisión, no necesitamos preocuparnos por la energía potencial o el impulso potencial —toda la energía está en forma de reposo más energía cinética excepto en este corto intervalo, y todos los momentos son momentos cinéticos.

Debido al principio de relatividad, somos libres de considerar colisiones en cualquier marco de referencia conveniente. Luego podemos transformar los resultados a cualquier marco de referencia que queramos. En términos generales, el marco de referencia más conveniente a considerar es aquel en el que el impulso total de las dos partículas es cero. En aras de la simplicidad solo consideramos colisiones en una dimensión.

Colisiones elásticas

Figura 10.2: Colisiones elásticas unidimensionales de dos partículas en el centro del marco de momento como se ve en diagramas espacio-tiempo.

Supongamos una partícula con masa m ₁ y velocidad inicial u ₁ en el centro del marco de momento, es decir, el marco de referencia en el que el impulso total es cero, choca elásticamente con otra partícula de masa m ₂ con velocidad inicial u ₂. Los momentos de las dos partículas son

\[p_{1}=\frac{m_{1} u_{1}}{\left(1-u_{1}^{2} / c^{2}\right)^{1 / 2}} \quad p_{2}=\frac{m_{2} u_{2}}{\left(1-u_{2}^{2} / c^{2}\right)^{1 / 2}}\label{10.7}\]

En el centro del marco de impulso debemos tener

\[p_{1}=-p_{2}\label{10.8}\]

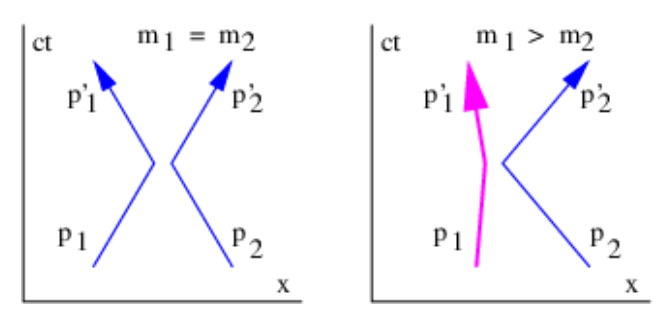
La Figura 10.2 muestra lo que sucede cuando estas dos partículas chocan. La primera partícula adquiere impulso p _1′ mientras que la segunda adquiere impulso p _2′. La conservación del impulso nos dice que el impulso total después de la colisión es el mismo que antes de la colisión, es decir, cero, entonces

\[p_{1}^{\prime}=-p_{2}^{\prime}\label{10.9}\]

En el centro del momentum frame lo sabemos\(\left|p_{1}\right|=\left|p_{2}\right|\) y sabemos que los dos vectores de impulso apuntan en direcciones opuestas. De igual manera,\(\left|p_{1}^{\prime}\right|=\left|p_{2}^{\prime}\right|\). Sin embargo, todavía no sabemos cómo\(p_{1}^{\prime}\) se relaciona con la p ₁. Conservación de energía,

\[E_{1}+E_{2}=E_{1}^{\prime}+E_{2}^{\prime}\label{10.10}\]

nos da esta información. Observe que si\(\mathrm{p}_{1}{ }^{\prime}=-\mathrm{p}_{1} \text { , then } \mathrm{E}_{1}{ }^{\prime 2}=\mathrm{p}_{1}{ }^{\prime 2} \mathrm{c}^{2}+\mathrm{m}_{1}{ }^{2} \mathrm{c}^{4}=\mathrm{p}_{1}{ }^{2} \mathrm{c}^{2}+\mathrm{m}_{1}^{2} \mathrm{c}^{4}=\mathrm{E}_{1}^{2}\). Asumiendo energías positivas, por lo tanto tenemos\(\mathrm{E}_{1}{ }^{\prime}=\mathrm{E}_{1} . \text { If } \mathrm{p}_{2}{ }^{\prime}=-\mathrm{p}_{2}\), entonces podemos inferir de manera similar eso\(\mathrm{E}_{2}{ }^{\prime}=\mathrm{E}_{2}\). Si se cumplen estas condiciones, entonces también lo es la ecuación (\ ref {10.10}). Por lo tanto, una solución completa al problema es

\[p_{1}=-p_{1}^{\prime}=-p_{2}=p_{2}^{\prime} \equiv p\label{10.11}\]

y

\[E_{1}=E_{1}^{\prime}=\left(p^{2} c^{2}+m_{1}^{2} c^{4}\right)^{1 / 2} \quad E_{2}=E_{2}^{\prime}=\left(p^{2} c^{2}+m_{2}^{2} c^{4}\right)^{1 / 2}\label{10.12}\]

En otras palabras, las partículas simplemente intercambian momentos.

El panel izquierdo de la figura 10.2 muestra lo que sucede en una colisión cuando las masas de las dos partículas colisionantes son iguales. Si\(m_{1}=m_{2}\), entonces las velocidades de entrada y salida de las dos partículas son las mismas, como lo indican las pendientes inversas de las líneas mundiales. Por otro lado, si\(m_{1}>m_{2}\), entonces la velocidad de la partícula 2 es mayor que la velocidad de la partícula 1, como se ilustra en el panel derecho de la figura 10.2.

Figura 10.3: Colisiones elásticas vistas desde un marco de referencia en el que una partícula está inicialmente estacionaria.

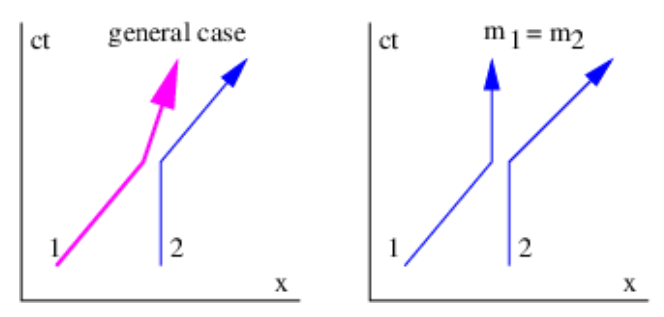
Supongamos que deseamos ver los resultados de una colisión elástica en un marco de referencia en el que la partícula 2 es inicialmente estacionaria. Todo lo que tenemos que hacer es transformar las velocidades en un marco de referencia que se mueve con la velocidad inicial de la partícula 2, como se ilustra en la figura 10.3. Esto lo hacemos sumando relativisticamente\(U=-u_{2}\) a cada velocidad. (Tenga en cuenta que la velocidad U del cuadro móvil es positiva ya que\(\mathrm{u}_{2}\) es negativa). Usando la fórmula relativista de traducción de velocidad, encontramos que

\[v_{1}=\frac{u_{1}+U}{1+u_{1} U / c^{2}} \quad v_{1}^{\prime}=\frac{u_{1}^{\prime}+U}{1+u_{1}^{\prime} U / c^{2}} \quad v_{2}^{\prime}=\frac{u_{2}^{\prime}+U}{1+u_{2}^{\prime} U / c^{2}}\label{10.13}\]

donde\(\mathrm{u}_{1}, \mathrm{u}_{1}^{\prime}, \mathrm{u}_{2}, \text { and } \mathrm{u}_{2}{ }^{\prime}\) indican velocidades en el marco de referencia original, centro de momento y v ₁, v ₁ ′, etc., indican velocidades en el marco transformado.

En el caso especial donde las masas de las dos partículas son iguales entre sí, tenemos\(\mathrm{v}_{1}=2 \mathrm{U} /\left(1+\mathrm{U}^{2} / \mathrm{c}^{2}\right), \mathrm{v}_{1}{ }^{\prime}=0, \text { and } \mathrm{v}_{2}{ }^{\prime}=2 \mathrm{U} /\left(1+\mathrm{U}^{2} / \mathrm{c}^{2}\right)=\mathrm{v}_{1}\). Así, cuando las masas son iguales, las partículas simplemente intercambian velocidades.

Si las velocidades son no relativistas, entonces se\(v=u+U\) puede usar la ley de transformación galileana más simple en lugar de las ecuaciones relativistas invocadas anteriormente.

Colisiones inelásticas

Figura 10.4: Bloques de construcción de colisiones inelásticas. En el panel izquierdo chocan dos partículas para formar una tercera partícula. En el panel derecho se rompe una partícula, formando dos partículas.

Una colisión inelástica es aquella en la que las partículas que salen de la colisión no son las mismas que las partículas que entran en ella. Las colisiones inelásticas conservan tanto el impulso total como la energía tal como lo hacen las colisiones elásticas. Sin embargo, a diferencia de las colisiones elásticas, las colisiones inelásticas generalmente no conservan la energía cinética total de las partículas, ya que generalmente se crea o destruye alguna energía de reposo.

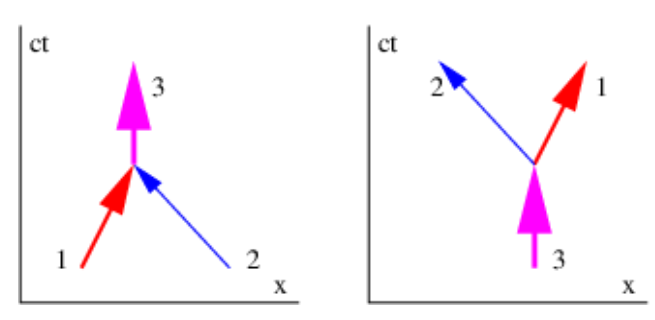
La Figura 10.4 muestra los bloques de construcción fundamentales de las colisiones inelásticas. Podemos considerar que incluso las colisiones inelásticas más complejas están compuestas por compuestos de solo dos procesos, la creación de una partícula a partir de dos, y la desintegración de una partícula en dos.

Consideremos cada uno de estos en el centro del marco de impulso. En ambos casos la partícula única debe ser estacionaria en este marco ya que lleva el impulso total del sistema, que tiene que ser cero. Por conservación del momento, si la partícula 1 en el panel izquierdo de la figura 10.4 tiene impulso p, entonces el impulso de la partícula 2 es -p. Si las dos partículas tienen masas m ₁ y m ₂, entonces sus energías son\(E_{1}=\left(p^{2} c^{2}+m_{1}^{2} c^{4}\right)^{1 / 2} \text { and } E_{2}=\left(p^{2} c^{2}+m_{2}^{2} c^{4}\right)^{1 / 2}\). La energía de la partícula 3 es por lo tanto\(\mathrm{E}_{3}=\mathrm{E}_{1}+\mathrm{E}_{2}\), y como está en reposo, toda su energía está en forma de “\(\mathrm{mc}^{2}\)” o energía de reposo, y así la masa de esta partícula es

\ [\ begin {ecuación}
\ begin {alineado}
m_ {3} &=\ left (E_ {1} +E_ {2}\ right)/c^ {2}\ quad (\ text {centro de momentum frame})\\
&=\ izquierda (p^ {2}/c^ {2} +m_ {1} ^ {2}\ derecha) ^ {1/2} + izquierda\ (p^ {2}/c^ {2} +m_ {2} ^ {2}\ derecha) ^ {1/2}\\
&=m_ {1}\ izquierda [1+p^ {2}/\ izquierda (m_ {1} ^ {2} c^ {2}\ derecha)\ derecha] ^ {1/2} +m_ {2}\ izquierda [1+p^ {2}/\ izquierda (m_ {2} ^ {2} c^ {2}\ derecha)\ derecha] ^ {1/2}
\ final {alineado}
\ final {ecuación}\ etiqueta {10.14}\]

La última línea de la ecuación anterior muestra que\(m_{3}>m_{1}+m_{2}\) porque está en la forma\(m_{1} A+m_{2} B\) donde tanto A como B son mayores que uno. Así, la energía de descanso se crea en la cantidad\(\Delta \mathrm{E}_{\text {rest }}=\left(m_{3}-m_{1}-m_{2}\right) c^{2}\).

En realidad, es fácil calcular la masa de la partícula 3 en el caso anterior a partir de cualquier marco de referencia siempre y cuando se conozcan los momentos y energías de las partículas 1 y 2 en este marco. Por conservación de energía e impulso,\(\mathrm{E}_{3}=\mathrm{E}_{1}+\mathrm{E}_{2} \text { and } \mathbf{p}_{3}=\mathbf{p}_{1}+\mathbf{p}_{2}\). Además\(\mathrm{E}_{3}^{2}=\mathrm{p}_{3}^{2} \mathrm{c}^{2}+\mathrm{m}_{3}^{2} \mathrm{c}^{4}\), así podemos resolver para m ₃:

\[m_{3}=\left[\left(E_{1}+E_{2}\right)^{2} / c^{4}-\left(\mathbf{p}_{1}+\mathbf{p}_{2}\right) \cdot\left(\mathbf{p}_{1}+\mathbf{p}_{2}\right) / c^{2}\right]^{1 / 2} \quad(\text { any frame })\label{10.15}\]

El panel derecho de la figura 10.4 muestra el proceso de descomposición de las partículas. Esto es solo lo inverso del proceso de creación de partículas, y todo el análisis que hemos hecho para la creación es válido para la descomposición de las partículas excepto que la energía de reposo se convierte en energía cinética en lugar de viceversa.