10.5: Cohetes y Cintas Transportadoras

Normalmente cuando definimos un sistema al que se va a aplicar la segunda ley de Newton, el sistema se cierra en el sentido de que la masa no puede entrar o salir del sistema. No obstante, a veces es conveniente trabajar con sistemas abiertos para los cuales esto no es cierto. El ejemplo clásico es el cohete, donde los gases de escape salen del sistema, disminuyendo así la masa del cohete con el tiempo.

Los sistemas abiertos pueden analizarse si se considera que el impulso es una cantidad que se contabiliza tanto como el dinero se contabiliza en una cuenta bancaria. La cuenta bancaria puede cambiar de tres maneras: el dinero se puede depositar en la cuenta, se puede retirar de la cuenta y el monto puede crecer o reducirse como consecuencia de pagos de intereses o comisiones. De igual manera, la cantidad de impulso en un sistema puede cambiar como resultado de la entrada de masa al sistema, la masa que sale del sistema y las fuerzas que actúan sobre el sistema. La tasa de tiempo de cambio de impulso en un sistema es por lo tanto

\[\frac{d p}{d t}=F+\left(\frac{d p}{d t}\right)_{i n}-\left(\frac{d p}{d t}\right)_{o u t}\label{10.16}\]

donde F es la fuerza neta en el sistema,\((\mathrm{dp} / \mathrm{dt})_{\mathrm{in}}\) es el impulso por unidad de tiempo agregado por la masa que ingresa al sistema, y\(\text { (dp /dt) }_{\text {out }}\) es la cantidad perdida por unidad de tiempo por masa que sale del sistema. En el caso no relativista,\((\mathrm{dp} / \mathrm{dt})_{\mathrm{in}}=\mathrm{u}_{\mathrm{in}}(\mathrm{dm} / \mathrm{dt})_{\mathrm{in}} \text { and }(\mathrm{dp} / \mathrm{dt})_{\mathrm{out}}=\mathrm{u}_{\mathrm{out}}(\mathrm{dm} / \mathrm{dt})_{\mathrm{out}}\), donde\((\mathrm{dm} / \mathrm{dt})_{\mathrm{in}}\) está la masa que ingresa al sistema por unidad de tiempo con velocidad u _adentro y\((\mathrm{dm} / \mathrm{dt})_{\mathrm{out}}\) es la masa por unidad de tiempo que sale del sistema con velocidad\(\mathrm{u}_{\mathrm{out}}\).

Para velocidades no relativistas, el impulso del sistema puede escribirse de\(p = mu\) manera que

\[\frac{d p}{d t}=\frac{d m}{d t} u+m \frac{d u}{d t}\label{10.17}\]

Para completar el análisis, necesitamos una contabilidad de la masa que ingresa y sale del sistema:

\[\frac{d m}{d t}=\left(\frac{d m}{d t}\right)_{i n}-\left(\frac{d m}{d t}\right)_{o u t}\label{10.18}\]

Figura 10.5: Cohete que se mueve con velocidad V mientras expulsa gas a una velocidad R con velocidad V - u _x.

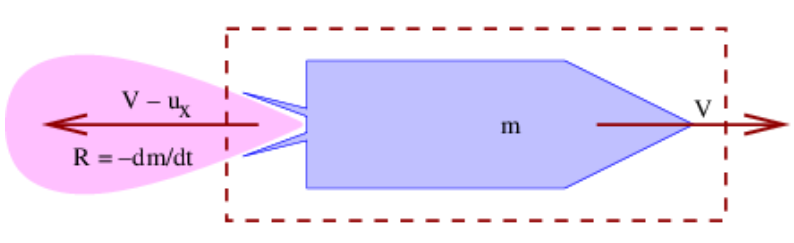
Veamos cómo aplicar esto a un cohete para el que todas las velocidades son no relativistas. Como indica la figura 10.5, un cohete arroja una corriente de gases de escape. El sistema está definido por la caja discontinua e incluye el cohete y la parte del gas de escape dentro de la caja. La reacción al impulso arrastrado en esta corriente de gas es lo que hace que el cohete acelere. Observamos que\((\mathrm{dm} / \mathrm{dt})_{\mathrm{in}}=0\) dado que ninguna masa está entrando al sistema, y\((\mathrm{dm} / \mathrm{dt})_{\mathrm{out}}=\mathrm{R}\), la velocidad a la que la masa es expulsada por el cohete en forma de gas de escape. Se supone que el cohete se mueve hacia la derecha a la velocidad V y el gas es expulsado a una velocidad u _x relativa al cohete, lo que significa que su velocidad real después de la expulsión es V - u _x. Llamamos a u _x la velocidad de escape. Observe que V - u _x puede ser positivo o negativo, dependiendo de qué tan grande sea V.

Equiparando la masa del cohete con la masa del sistema, lo encontramos\(\mathrm{R}=-\mathrm{dm} / \mathrm{dt}\). La ecuación del balance de impulso (\ ref {10.16}) se convierte en\(\mathrm{dp} / \mathrm{dt}=-\left(\mathrm{V}-\mathrm{u}_{\mathrm{x}}\right) \mathrm{R}\). La fuerza sobre el cohete es en realidad cero, por lo que el término de fuerza no entra en la ecuación del balance de impulso. Esto no es intuitivo, porque estamos acostumbrados a que la aceleración sea el resultado de una fuerza. Sin embargo, nada, incluido el gas expulsado, en realidad está presionando al sistema, por lo que de hecho debemos concluir que no hay fuerza —todo el cambio en el impulso del sistema surge de la expulsión de gas con el impulso opuesto.

Por último, eso lo vemos\(\mathrm{dp} / \mathrm{dt}=(\mathrm{dm} / \mathrm{dt}) \mathrm{V}+\mathrm{m}(\mathrm{dV} / \mathrm{dt})=-\mathrm{RV}+\mathrm{m}(\mathrm{dV} / \mathrm{dt})\). Equiparar esto con los resultados del cálculo del balance de impulso nos da\(-\mathrm{RV}+\mathrm{m}(\mathrm{d} \mathrm{V} / \mathrm{dt})=-\left(\mathrm{V}-\mathrm{u}_{\mathrm{X}}\right) \mathrm{R}\). Resolviendo para los\(\mathrm{dV} / \mathrm{dt}\) resultados de aceleración en

\[\frac{d V}{d t}=\frac{u_{x} R}{m} \quad \text { (rocket acceleration) }\label{10.19}\]

Así, la aceleración del cohete depende de la velocidad de escape del gas expulsado, la velocidad a la que se está expulsando el gas y la masa del cohete.

Figura 10.6: La arena se arroja sobre una cinta transportadora y a su vez se arroja del extremo de la cinta.

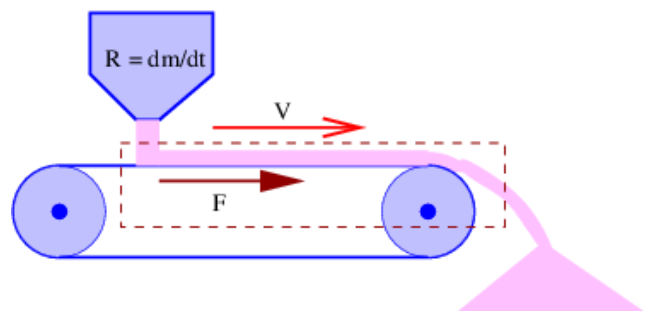
La Figura 10.6 ilustra otro tipo de problema de sistema abierto. Una tolva arroja arena sobre una cinta transportadora a razón de R kilogramos por segundo. La cinta transportadora se mueve hacia la derecha a una velocidad V (no relativista) y la arena se desecha al final. ¿Qué fuerza F se necesita para mantener la cinta transportadora en movimiento a una velocidad constante, suponiendo que el mecanismo de la cinta transportadora en sí no tiene fricción? En este caso\((\mathrm{dm} / \mathrm{dt})_{\mathrm{in}}=(\mathrm{dm} / \mathrm{dt})_{\text {out }}=\mathrm{R}\). Además, dado que el sistema delineado por la línea discontinua está en un estado estacionario,\(\mathrm{dp} / \mathrm{dt}=0\).

La clave para entender este problema es que la arena ingresa al sistema con velocidad horizontal cero, pero sale del sistema con la velocidad horizontal de la cinta transportadora, V. La ecuación del balance de impulso es así

\[0=F-V R\label{10.20}\]

y la fuerza es

\[F=V R \text { (force on conveyor belt). }\label{10.21}\]

Esta fuerza sirve para acelerar la arena hasta la velocidad de la cinta transportadora.