11.3: Dos Partículas

Figura 11.5: Dos partículas de masa M ₁ y M ₂ con M ₂ > M ₁.

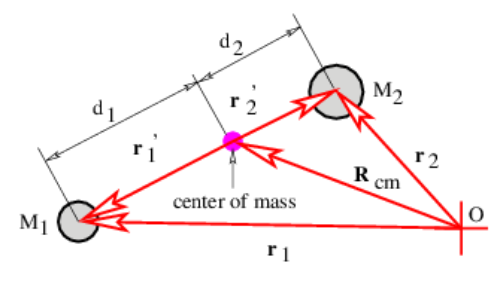
Supongamos que deseamos aplicar la segunda ley de Newton a dos partículas consideradas juntas como un solo sistema. Como mostramos anteriormente, solo las fuerzas externas actúan sobre el impulso total, p _total = p ₁ + p ₂, de las dos partículas:

\[\mathbf{F}_{\text {external }}=\frac{d \mathbf{p}_{\text {total }}}{d t}\label{11.9}\]

Escribamos el impulso no relativista total de las dos partículas de una manera especial:

\[\mathbf{p}_{\text {total }}=M_{1} \mathbf{v}_{1}+M_{2} \mathbf{v}_{2}=M_{\text {total }}\left(\frac{M_{1} \mathbf{v}_{1}+M_{2} \mathbf{v}_{2}}{M_{\text {total }}}\right) \equiv M_{\text {total }} \mathbf{V}_{c m}\label{11.10}\]

donde\(\mathrm{M}_{\text {total }}=\mathrm{M}_{1}+\mathrm{M}_{2}\). La cantidad\(\mathbf{V}_{\mathrm{cm}}\) es la velocidad del centro de masa y puede expresarse como la derivada temporal de la posición del centro de masa\(\mathbf{R}_{\mathrm{Cm}}\),

\[\mathbf{V}_{c m}=\frac{d \mathbf{R}_{c m}}{d t}\label{11.11}\]

donde

\[\mathbf{R}_{c m}=\frac{M_{1} \mathbf{r}_{1}+M_{2} \mathbf{r}_{2}}{M_{\text {total }}}\label{11.12}\]

Ahora vemos cómo la energía cinética y el momento angular de las dos partículas pueden dividirse en dos partes, una teniendo que ver con el movimiento del centro de masa de las dos partículas, la otra teniendo que ver con el movimiento de las dos partículas relativo a su centro de masa. La Figura 11.5 muestra gráficamente cómo \(se definen los vectores. Estos vectores\ (\ mathbf {r} _ {1} ^ {\ prime} =\ mathbf {r} _ {1} -\ mathbf {R} _ {\ mathrm {cm}}\ text {y}\ mathbf {r} _ {2} ^ {\ prime} =\ mathbf {r} _ {2} -\ mathbf {R} _ {\ mathrm {cm}}\) representan las posiciones de las dos partículas con respecto al centro de masa. La sustitución en la ecuación (\ ref {11.12}) lo demuestra\(\mathrm{M}_{1} \mathbf{r}_{1}^{\prime}+\mathrm{M}_{2} \mathbf{r}_{2}^{\prime}=0\). Esto lleva a la conclusión de que\(\mathrm{M}_{1} \mathrm{~d}_{1}=\mathrm{M}_{2} \mathrm{~d}_{2}\) en la figura 11.5. También definimos la velocidad de cada masa en relación con el centro de masa como\(\mathbf{v}_{1}^{\prime}=\mathrm{d} \mathbf{r}^{\prime}{ }_{1} / \mathrm{d} \mathrm{t} \text { and } \mathbf{v}_{2}^{\prime}=\mathrm{d} \mathbf{r}^{\prime}{ }_{2} / \mathrm{dt}\), y por lo tanto tenemos\(\mathrm{M}_{1} \mathbf{v}_{1}^{\prime}+\mathrm{M}_{2} \mathbf{v}_{2}^{\prime}=0\).

La energía cinética total es solo la suma de las energías cinéticas de las dos partículas\(\mathrm{K}=\mathrm{M}_{1} \mathrm{v}_{1}^{2} / 2+\mathrm{M}_{2} \mathrm{v}_{2}^{2} / 2\), donde v ₁ y v ₂ son las magnitudes de los vectores de velocidad correspondientes. Sustitución de\(\mathbf{v}_{1}=\mathbf{V}_{\mathrm{cm}}+\mathbf{v}_{1}^{\prime}\) etc., en la fórmula de energía cinética y reorganización de los rendimientos

\[K_{\text {total }}=K_{\text {trans }}+K_{\text {intern }}=\left[M_{\text {total }} V_{c m}^{2} / 2\right]+\left[M_{1} v_{1}^{\prime 2} / 2+M_{2} v_{2}^{\prime 2} / 2\right] .\label{11.13}\]

Términos como\(\mathbf{V}_{c m} \cdot \mathbf{v}_{1}^{\prime}\) cancelar porque\(M_{1} \mathbf{v}_{1}^{\prime}+M_{2} \mathbf{v}_{2}^{\prime}=0\).

El primer término en el lado derecho de la ecuación (\ ref {11.13}) entre corchetes es la energía cinética que tendrían las dos partículas si toda la masa estuviera concentrada en el centro de masa. El segundo término es la energía cinética calculada en relación con el movimiento del centro de masa. El primero se llama la energía cinética traslacional del sistema mientras que el segundo se llama la energía cinética interna.

El momento angular del sistema es solo la suma de los momentos angulares de las dos partículas:\(\mathbf{L}_{\text {total }}=\mathbf{M}_{1} \mathbf{r}_{1} \times \mathbf{v}_{1}+\mathbf{M}_{2} \mathbf{r}_{2} \times \mathbf{v}_{2}\). Razonando similar al caso de la energía cinética, podemos reescribir esto como

\[\mathbf{L}_{\text {total }}=\mathbf{L}_{\text {orb }}+\mathbf{L}_{\text {spin }}=\left[M_{\text {total }} \mathbf{R}_{c m} \times \mathbf{V}_{c m}\right]+\left[M_{1} \mathbf{r}_{1}^{\prime} \times \mathbf{v}_{1}^{\prime}+M_{2} \mathbf{r}_{2}^{\prime} \times \mathbf{v}_{2}^{\prime}\right]\label{11.14}\]

El primer término entre corchetes a la derecha se denomina momento angular orbital mientras que el segundo término se denomina momento angular de giro. El primero es el momento angular que tendría el sistema si toda la masa se concentrara en el centro de masa, mientras que el segundo es el momento angular de movimiento alrededor del centro de masa.

Curiosamente, la idea del centro de masa y la correspondiente división de la energía cinética y el momento angular en partes orbitales y espinas no tiene una generalización relativista útil. Esto se debe al factor de\(\gamma \equiv\left(1-v^{2} / c^{2}\right)^{-1 / 2}\) en la definición relativista de impulso\(\mathbf{p}=m \mathbf{v} \gamma\), lo que significa que

\[\frac{d m \mathbf{r}}{d t} \neq \mathbf{p} \quad \text { (relativistic case). }\label{11.15}\]