11.4: La Mancuerna Desigual

Última actualización
Guardar como PDF

Page ID: 125985

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

Figura 11.6: Vista en perspectiva de la mancuerna giratoria unida a un eje etiquetado\(\omega\). El eje se fija al travesaño en el centro de masa. La velocidad v ₁ está fuera de la página y v ₂ está dentro de la página.

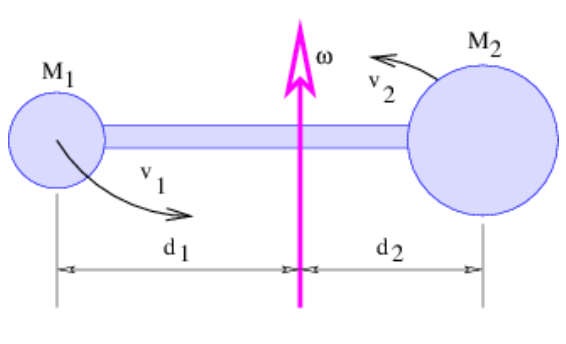
Hasta el momento no hemos puesto restricciones a los movimientos de las dos partículas. Un caso especial interesante ocurre cuando las partículas están conectadas por una varilla ligera y rígida, dándonos una mancuerna. Para simplificar aún más las cosas, suponemos que la varilla está conectada rígidamente a un eje fijo en el centro de masa de las dos partículas, como se muestra en la figura 11.6. Por lo tanto, las masas que constituyen los extremos de la mancuerna son libres de girar en círculos alrededor del eje, pero se les impide ejecutar cualquier otro movimiento. El efecto clave de esta restricción es que ambas masas giran alrededor del eje con la misma frecuencia angular\(\omega\).

Si las partículas están respectivamente a distancias d ₁ y d ₂ del eje, entonces sus velocidades son\(\mathrm{v}_{1}=\mathrm{d}_{1} \omega \text { and } \mathrm{v}_{2}=\mathrm{d}_{2} \omega\). Así, la energía cinética de la mancuerna giratoria es

\[K_{\text {intern }}=\frac{1}{2} M_{1} v_{1}^{2}+\frac{1}{2} M_{2} v_{2}^{2}=\frac{1}{2} I \omega^{2} \quad \text { (fixed axle) }\label{11.16}\]

donde\(I=M_{1} d_{1}^{2}+M_{2} d_{2}^{2}\) se llama el momento de inercia. Del mismo modo, la magnitud del momento angular de giro, que es un vector paralelo al eje, es

\[L_{s p i n}=M_{1} d_{1} v_{1}+M_{2} d_{2} v_{2}=I \omega \quad \text { (fixed axle) }\label{11.17}\]

Finalmente, la segunda ley de Newton para la rotación se convierte en

\[\tau=\frac{d L_{s p i n}}{d t}=\frac{d I \omega}{d t}=I \frac{d \omega}{d t} \quad(\text { fixed axle })\label{11.18}\]

donde\(\tau\) es el componente del par a lo largo del eje de rotación.

Tenga en cuenta que la expresión más a la derecha en la ecuación (\ ref {11.18}) asume que I es constante, lo cual solo es cierto si d ₁ y d ₂ son constantes — i. e., la mancuerna debe ser realmente rígida.