12.3: Oscilador Forzado

Última actualización
Guardar como PDF

Page ID: 126049

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

Figura 12.3: Ilustración de un oscilador de masa-resorte forzado. El extremo izquierdo del resorte se mueve hacia adelante y hacia atrás con una frecuencia angular\(\omega_{F}\) y una amplitud máxima\(\mathrm{d}_{0}\).

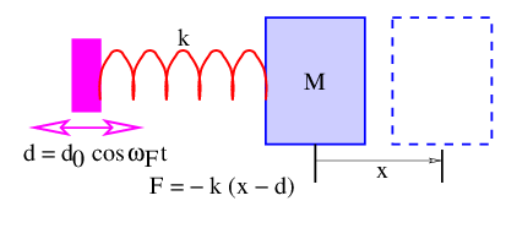
Si meneamos el extremo izquierdo del resorte por la cantidad\(\mathrm{d}=\mathrm{d}_{0} \cos \left(\omega_{\mathrm{F}} \mathrm{t}\right)\), como en la figura 12.3, en lugar de fijarlo rígidamente como en la figura 12.1, tenemos un oscilador armónico forzado. La constante\(\mathrm{d}_{0}\) es la amplitud del movimiento de meneo impuesto. La frecuencia de forzamiento no\(\omega_{F}\) es necesariamente igual a la frecuencia natural o resonante\(\omega=(\mathrm{k} / \mathrm{M})^{1 / 2}\) del sistema masa-resorte. Comportamiento muy diferente ocurre dependiendo de si\(\omega_{F}\) es menor que, igual o mayor que\(\omega\).

Dado el meneo anterior, la fuerza del resorte sobre la masa se vuelve\(F=-k(x-d)=-k\left[x-d_{0} \cos \left(\omega_{F} t\right)\right]\) ya que la longitud del resorte es la diferencia entre las posiciones de los extremos izquierdo y derecho. Procediendo en cuanto al sistema masa-resorte no forzado, llegamos a la ecuación diferencial

\[\frac{d^{2} x}{d t^{2}}+\frac{k x}{M}=\frac{k d_{0}}{M} \cos \left(\omega_{F} t\right)\label{12.10}\]

La solución a esta ecuación resulta ser la suma de una parte forzada en la que\(x\) es proporcional\(\cos \left(\omega_{F} t\right)\) y una parte libre que es la misma que la solución a la ecuación no forzada (12.2.4). Nos interesa principalmente la parte forzada de la solución, así que pongamos\(x=x_{0} \cos \left(\omega_{F} t\right)\) y sustituyamos esto en ecuación (\ ref {12.10}):

\[-\omega_{F}^{2} x_{0} \cos \left(\omega_{F} t\right)+\frac{k x_{0}}{M} \cos \left(\omega_{F} t\right)=\frac{k d_{0}}{M} \cos \left(\omega_{F} t\right)\label{12.11}\]

Nuevamente el factor coseno cancela y nos quedamos con una ecuación algebraica para x ₀, la amplitud del movimiento oscilatorio de la masa.

Figura 12.4: Gráfica de la relación de respuesta a forzamiento vs. la relación entre la frecuencia del oscilador forzado y libre para el sistema masa-resorte.

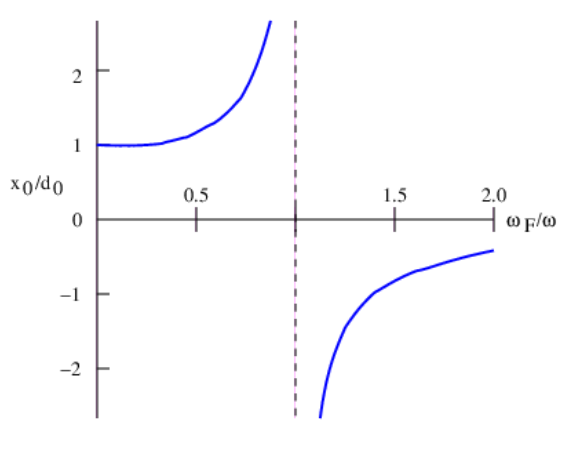
Resolviendo la relación de la amplitud de oscilación de la masa a la amplitud del movimiento de meneo\(\mathrm{x}_{0} / \mathrm{d}_{0}\),, encontramos

\[\frac{x_{0}}{d_{0}}=\frac{1}{1-\omega_{F}^{2} / \omega^{2}}\label{12.12}\]

donde hemos reconocido eso\(k / M=\omega^{2}\), el cuadrado de la frecuencia de la oscilación libre. Esta función se representa en la figura 12.4.

Observe que si\(\omega_{F}<\omega_{1}\), el movimiento de la masa está en fase con el movimiento de meneo y la amplitud de la oscilación de masa es mayor que la amplitud del movimiento. A medida que la frecuencia de forzamiento se acerca a la frecuencia natural del oscilador, la respuesta de la masa crece en amplitud. Cuando el forzamiento está a la frecuencia resonante, la respuesta es técnicamente infinita, aunque en este caso intervendrán límites prácticos sobre la amplitud de la oscilación —por ejemplo, el resorte no puede estirarse ni encogerse una cantidad infinita. En muchos casos la fricción actuará para limitar la respuesta de la masa a forzar cerca de la frecuencia resonante. Cuando la frecuencia de forzamiento es mayor que la frecuencia natural, la masa realmente se mueve en la dirección opuesta al movimiento de meneo, es decir, la respuesta está desfasada con el forzamiento. La amplitud de la respuesta disminuye a medida que la frecuencia de forzamiento aumenta por encima de la frecuencia resonante.

Los osciladores armónicos forzados y libres forman una parte importante de muchos sistemas físicos. Por ejemplo, cualquier cuerpo de material elástico como un puente o un ala de avión tiene modos oscilatorios armónicos. Un problema común de ingeniería es asegurar que dichos modos sean amortiguados por fricción o algún otro mecanismo físico cuando existe la posibilidad de que estos modos salgan por procesos naturales. Una serie de desastres se puede rastrear a una falla en explicar adecuadamente el forzamiento oscilatorio en estructuras de ingeniería.