10.5: Efectos de la Rotación de la Tierra- Fuerzas Aparentes

Las leyes de Newton se aplican en un marco de referencia inercial, es decir, uno que no está acelerando. Un punto en la Tierra giratoria no está siguiendo una línea recta a través del espacio, sino que está acelerando constantemente rotando alejándose de una línea recta. Por lo tanto, la Tierra no proporciona un marco de referencia inercial. Desde el punto de vista de un astronauta en el espacio distante, los movimientos aéreos que observaría obedecen perfectamente a la Ley de Newton, pero desde el punto de vista de un observador con destino a la Tierra, las Leyes de Newton no logran captar el movimiento observado. Para dar cuenta de este comportamiento loco, el observador con destino a la Tierra necesita agregar algunas fuerzas aparentes a las fuerzas reales para que las matemáticas expliquen el movimiento observado desde el punto de vista de alguien parado en la Tierra giratoria.

La rotación de la Tierra es hacia el este. El símbolo indica que el vector\(\vec{U}_{e}\) s va a la página con una magnitud RΩ. Crédito: W. Brune

Supongamos que tenemos una parcela aérea moviéndose por el espacio con una velocidad\(\vec{U}_{a}\), a la que llamaremos la velocidad absoluta. Queremos relacionar esta velocidad absoluta con la velocidad observada con respecto al marco de referencia de la Tierra.\(\vec{U}\) \(\vec{U}_{e}\)Sea la velocidad de la Tierra. Aquí solo consideramos la velocidad de la Tierra debido a la rotación alrededor de su eje (el movimiento alrededor del Sol es mucho menos importante), por lo que siempre\(\vec{U}_{e}\) es hacia el este, mayor en el ecuador y cero en los polos. La velocidad absoluta de un paquete aéreo es simplemente la velocidad de la parcela aérea con respecto a la Tierra más la velocidad de la Tierra misma:\(\vec{U}_{a}=\vec{U}+\vec{U}_{e}\)

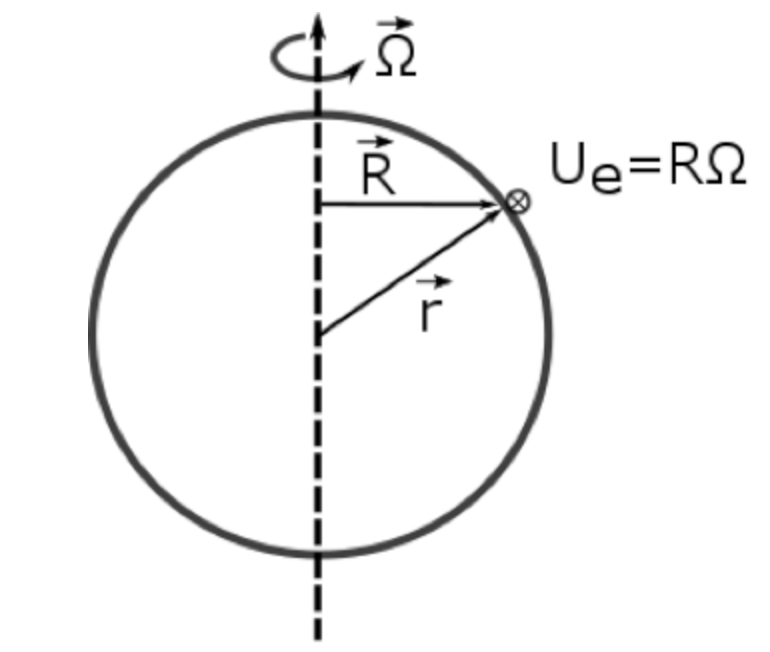
¿Cuál es la velocidad de la Tierra? Considera un punto específico en la Tierra. \(\vec{\Omega}\)Sea el vector de velocidad angular de la Tierra,\(\vec{r}\) sea el vector de posición desde el centro de la Tierra hasta el punto en cuestión, y\(\vec{R}\) ser el vector de distancia más corta desde el eje de rotación hasta el punto en cuestión (como en la figura anterior). La magnitud\(\vec{\Omega} \text { is }|\vec{\Omega}|=\frac{2 \pi}{23.934 \mathrm{hr}} \frac{1 \mathrm{hr}}{3600 \mathrm{s}}=7.292 \times 10^{-5} \mathrm{s}^{-1}\) y la dirección de\(\vec{\Omega}\) está determinada por la regla de la mano derecha (la dirección de tu pulgar cuando rizas los dedos de tu mano derecha en la dirección de rotación y apuntas tu pulgar hacia la Estrella del Norte). Para determinar la velocidad angular de la Tierra, tenga en cuenta que hemos utilizado la duración del día sideral, 23.934 hr, que es la duración del día cuando se mide la rotación de la Tierra con respecto a las estrellas fijas (el marco de referencia inercial).

El siguiente video (:51) demostrará la regla de la mano derecha:

Regla de la Mano Derecha UE

Haga clic aquí para ver la transcripción del video de la regla de la mano derecha de la UE

u sub e es la velocidad hacia el este de la Tierra. Se señala en la página. Sabemos que el u sub e es igual a r— que es el vector de distancia más corta entre el eje de rotación de la Tierra y el punto en la superficie— por omega, que es el vector de rotación de la Tierra. Las unidades de omega son segundos al menos 1, lo que lo convierte en una frecuencia. Tenga en cuenta que u sub e es igual a r por omega, que también es igual a omega cruz r. podemos ver esto si tomas tu mano derecha con los dedos apuntando en la dirección omega y la palma en la dirección r. Y doblas los dedos en la palma de la mano. Tu pulgar apuntará a la página, que es la dirección de u sub e y está en la dirección x positiva.

La magnitud de\(\vec{U}_{e}\) es\(R \Omega,\) pero necesitamos escribir\(\vec{U}_{e}\) como vector. Obsérvese que\(\vec{U}_{e}\) se señala en la página en la figura anterior, que es una dirección perpendicular a ambos\(\vec{\Omega}\) y\(\vec{R}\). De ahí que podamos usar la ecuación de producto cruzado para escribir una expresión para la velocidad de la Tierra:\(\vec{U}_{e}=\vec{\Omega} \times \vec{R}=\vec{\Omega} \times \vec{r}\), ya que el componente de\(\vec{r}\) perpendicular a\(\vec{\Omega}\) es\(\vec{R} .\) So:

\[\vec{U}_{a}=\vec{U}+\vec{\Omega} \times \vec{r}\]

Por lo tanto, hemos relacionado la velocidad en el marco de referencia absoluta con la velocidad en el marco de referencia giratorio.
Ahora podemos considerar la aceleración. Ya\(\vec{U}=\frac{D \vec{r}}{D t} \text { and } \vec{U}_{a}=\frac{D_{a} \vec{r}}{D t}\) que podemos escribir:

\(\frac{D_{a} \vec{r}}{D t}=\frac{D \vec{r}}{D t}+\vec{\Omega} \times \vec{r}\)

Esta ecuación describe el cambio en una posición de una parcela aérea con el tiempo observado desde un marco de referencia inercial (la derivada de la izquierda) al cambio con el tiempo observado desde el marco de referencia de la Tierra (la derivada a la derecha). La ecuación [10.11] es general y se aplica no sólo a\(\vec{r}\) sino también a cualquier otro vector.

Reemplacemos\(\vec{r}\) en el lado izquierdo con\(\vec{U}_{a}\) y\(\vec{r}\) en el lado derecho con\(\vec{U}+\vec{\Omega} \times \vec{r}\) ya que estas dos expresiones se igualan entre sí en la Ecuación [10.10]. Al hacer estas sustituciones, podemos relacionar la aceleración en el cuadro absoluto con la aceleración en el marco giratorio:

\[\frac{D_{a} \vec{U}_{a}}{D t}=\frac{D \vec{U}}{D t}+\frac{\vec{D} \vec{\Omega}}{D t} \times \vec{r}+\vec{\Omega} \times \frac{D \vec{r}}{D t}+\vec{\Omega} \times \vec{U}+\vec{\Omega} \times(\vec{\Omega} \times \vec{r})\]

Podemos simplificar esta ecuación y luego podemos darle sentido físicamente. En primer lugar, no\(\vec{\Omega}\) está cambiando significativamente con el tiempo, por lo que se\(\frac{D \vec{\Omega}}{D t}\) puede establecer en cero. Segundo,\((\vec{\Omega} \times \vec{r})\) tiene la magnitud de ΩR y apunta hacia el este (por la regla de la mano derecha) y así\(\vec{\Omega} \times(\vec{\Omega} \times \vec{r})\) tiene la magnitud\(\Omega^{2} R\) y apunta hacia —\(\vec{R}\). Por último, señalando que\(\vec{U}=\frac{D \vec{r}}{D t}\), terminamos con la ecuación:

\[\frac{D_{a} \vec{U}_{a}}{D t}=\frac{D \vec{U}}{D t}+2 \vec{\Omega} \times \vec{U}-\Omega^{2} \vec{R}\]

El término a la izquierda es la aceleración en el marco de referencia inercial absoluto. El primer término a la derecha es la aceleración en el marco de referencia de la Tierra. Los términos restantes son las aparentes aceleraciones. El primero es la aceleración de Coriolis y el segundo es la aceleración centrípeta.

Ahora podemos combinar la Ecuación [10.13] con la versión de la Ecuación [10.9] que se promedia para obtener:

\[-\frac{1}{\rho} \vec{\nabla} p+\vec{g} *-\frac{C_{d}}{h}|\vec{V}| \vec{V}=\frac{D \vec{U}}{D t}+2 \vec{\Omega} \times \vec{U}-\Omega^{2} \vec{R}\]

y luego reorganizar esta ecuación para obtener:

\[\frac{D \vec{U}}{D t}=-\frac{1}{\rho} \vec{\nabla} p+\vec{g} *-\frac{C_{d}}{h}|\vec{V}| \vec{V}-2 \vec{\Omega} \times \vec{U}+\Omega^{2} \vec{R}\]

Los tres primeros términos del lado derecho de la Ecuación [10.14] son las fuerzas reales. El cuarto y quinto términos del lado derecho son las fuerzas aparentes: la fuerza Coriolis y la fuerza centrífuga, respectivamente.

Fuerza Centrífuga

La fuerza centrífuga se dirige alejándose del eje de rotación de la Tierra y es el mismo tipo de fuerza que sientes cuando estás en un automóvil dando la vuelta a una curva pronunciada. A lo largo de su larga historia, todo el material que conforma la Tierra se ha ajustado a la fuerza gravitacional real,\ vec {g} ^ {*}, que se dirige al centro de la Tierra, y a la aparente fuerza centrífuga que se dirige lejos del eje de rotación de la Tierra (ver figura abajo).

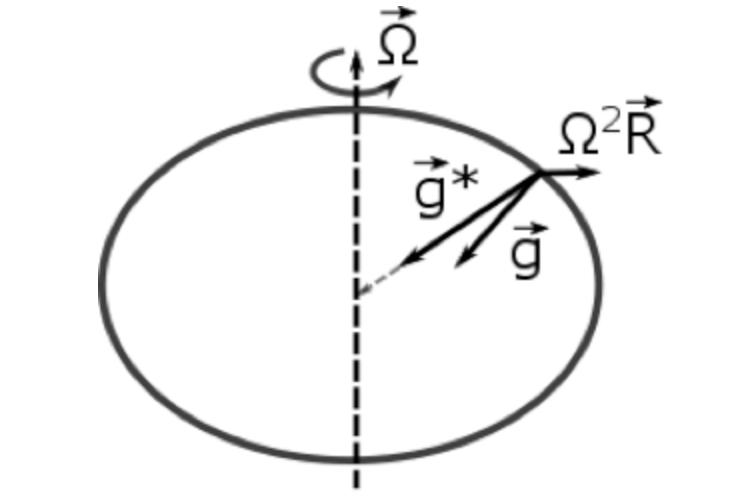
La gravedad que sentimos es la suma de gravedad apuntada hacia el centro de la Tierra y la fuerza centrífuga exterior. El efecto es muy exagerado para mostrar los vectores. La gravedad que sentimos\(\vec{g}\), es perpendicular a las superficies planas de la Tierra en reposo (es decir, océanos). Crédito: W. Brune

La gravedad resultante que siente la Tierra y todo sobre ella es la suma vectorial de esta fuerza real y aparente:

\[\vec{g}=\overrightarrow{g^{*}}+\Omega^{2} \vec{R}\]

Dado que la fuerza centrífuga depende\(\vec{R}\), es mayor en el ecuador y cero en los polos. Como resultado de la fuerza centrífuga, la Tierra se ha vuelto ligeramente oblata, con un radio ecuatorial de 6378.1 km que es 0.34% mayor que el radio polar de 6356.8 km. Obsérvese que siempre\(\overrightarrow{\boldsymbol{g}}\) es perpendicular a la superficie de la Tierra, lo cual es muy útil porque la coordenada vertical siempre se elige para que sea perpendicular a la superficie de la Tierra, por lo que\(\overrightarrow{\boldsymbol{g}}\) es solo en la dirección z y, como indica la figura anterior, no apunta hacia la centro de la Tierra (excepto en los polos y el ecuador). El valor de g en el ecuador es el\(9.780 \mathrm{ms}^{-2},\) cual es 0.052\(m s^{-2}\) menor que el valor de g en los polos, que es 9.832 m s ^—2. La fuerza centrífuga en el ecuador es\(\Omega^{2} R=\left(7.27 \times 10^{-5} \mathrm{s}^{-1}\right)^{2}\left(6.378 \times 10^{6} \mathrm{m}\right)=0.033 \mathrm{m} \mathrm{s}^{-2}\), y por lo tanto representa más casi 2/3 de la diferencia en g entre el ecuador y los polos. El resto de la diferencia se debe a la diferencia en g *, que está sobreestimada por la diferencia en radios ecuatoriales y polares; el problema es más complicado de lo que podría parecer porque la ley de gravitación de Newton solo se aplica a las masas puntuales. En cualquier caso, la diferencia entre g en los polos y el ecuador es lo suficientemente pequeña como para que un valor constante de g = 9.8 m s ^—2 sea adecuado para la mayoría de las aplicaciones en dinámica atmosférica.

La combinación de las ecuaciones [10.14] y [10.15] produce una forma más útil de la conservación promedio del momento en el marco de referencia giratorio:

\[\frac{\overrightarrow{D U}}{D t}=-\frac{1}{\rho} \vec{\nabla}_{p}+\vec{g}-\frac{C_{d}}{h}|\vec{V}| \vec{V}-2 \vec{\Omega} \times \vec{U}\]

Pasaremos ahora a una discusión sobre la Fuerza Coriolis. El siguiente video (3:05) da una introducción básica.

Efecto Coriolis

Haga clic aquí para ver la transcripción del video del Efecto Coriolis.

[REPRODUCCIÓN DE MÚSICA]

Si alguna vez has visto las noticias durante un huracán o Nor'easters invernales, probablemente hayas notado que las grandes tormentas giran con el tiempo a medida que viajan. En el hemisferio norte, giran en sentido antihorario. Pero si estuvieras viendo una tormenta en el hemisferio sur, la verías girando en el sentido de las agujas del reloj.

¿Por qué las tormentas giran en diferentes direcciones dependiendo de su ubicación y por qué giran en primer lugar? La rotación de una tormenta se debe a algo llamado efecto Coriolis, que es un fenómeno que hace que fluidos como el agua y el aire se curven a medida que viajan a través o sobre la superficie de la Tierra.

Aquí está la idea básica: la Tierra gira constantemente alrededor de su eje de oeste a este, pero debido a que la Tierra es una esfera y más ancha en el medio, los puntos en el ecuador en realidad están girando más rápido alrededor del eje que los puntos cercanos a los polos. Así que imagina que estabas parado en Texas y tenías un avión de papel mágico que podía recorrer cientos de kilómetros. Si tiraste tu avión directamente hacia el norte, podrías pensar que aterrizaría recto hacia el norte, tal vez en algún lugar de Nebraska.

Pero Texas en realidad está girando alrededor del eje de la Tierra más rápido que Nebraska porque está más cerca del ecuador. Eso significa que el avión de papel también está girando más rápido. Y cuando lo lanzas, se conserva ese impulso giratorio. Entonces, si tirabas tu avión de papel en línea recta hacia el norte, aterrizaría en algún lugar a la derecha de Nebraska, tal vez en Delaware.

Entonces, desde tu punto de vista en Texas, el avión habría tomado un camino curvo a la derecha. Lo contrario ocurriría en el hemisferio sur. Un objeto que viaja desde el ecuador hacia el sur sería desviado hacia la izquierda.

Entonces, ¿qué tiene que ver esto con que los huracanes giren? Bueno, en el centro de cada huracán hay una zona de muy baja presión. Como resultado, el aire de alta presión que rodea el centro, o el ojo de una tormenta, corre constantemente hacia el vacío de baja presión en el medio. Pero debido al efecto Coriolis, el aire que corre hacia el centro se desvía de rumbo.

En el hemisferio norte, los volúmenes de aire en todos los lados del ojo siguen tirándose ligeramente hacia la derecha. El aire sigue tratando de llegar a la mitad, y sigue desviándose, lo que hace que todo el sistema gire en sentido contrario a las agujas del reloj. En el hemisferio sur, donde el efecto Coriolis tira de aire hacia la izquierda, sucede lo contrario. Las tormentas giran alrededor del ojo en sentido horario.

Crédito: NOVA PBS

Fuerza Coriolis

La fuerza Coriolis\(-2 \vec{\Omega} \times \vec{U}\),, actúa sobre una parcela aérea (o cualquier otro objeto) sólo cuando se mueve con respecto a la Tierra. Actúa perpendicular al vector de velocidad angular de la Tierra y al vector de velocidad de la parcela aérea. La explicación de la fuerza de Coriolis suele dividirse en una explicación en la dirección zonal (latitud constante) y la dirección meridional (longitud constante).

Flujo zonal (velocidad del viento este-oeste)

Considera una parcela aérea que inicialmente está en reposo y en equilibrio hidrostático pero que se acelera impulsivamente a una velocidad u hacia el este (ver lado izquierdo de la figura a continuación). Inicialmente cuando estaba en reposo, tenía la misma aceleración que la Tierra debajo de ella. No obstante, después de que aceleró a la velocidad u, de pronto tuvo más aceleración de la que tenía antes, arrojándola fuera del equilibrio hidrostático. Observe el cambio en la aceleración que viene de que la parcela aérea adquiera repentinamente una velocidad hacia el este, que es solo la aceleración después de que la velocidad cambie menos la aceleración antes de que la velocidad cambie e iguale\((\Omega+u / R)^{2} R-\Omega^{2} R\). A una muy buena aproximación, este cambio equivale a la fuerza de Coriolis,\(2 \Omega u\).

Hay un componente vertical que apunta hacia arriba, pero también hay un componente horizontal de fuerza que apunta a la derecha del movimiento en el hemisferio norte y a la izquierda en el hemisferio sur.

Ahora considere una parcela aérea que inicialmente esté en reposo pero que se acelere impulsivamente a una velocidad u hacia el oeste (vea el lado derecho de la figura a continuación). La parcela aérea de repente tiene menos impulso angular que antes y experimenta una fuerza centrífuga disminuida. Esta disminución en el momento angular, a una muy buena aproximación, equivale a la fuerza Coriolis\(2 \Omega u\), pero apunta hacia el eje de rotación de la Tierra. Hay un componente vertical que apunta hacia abajo, pero el componente horizontal de fuerza que apunta a la derecha del movimiento en el hemisferio norte y a la izquierda en el hemisferio sur.

Coriolis fuerza sobre una parcela aérea que viaja zonalmente (izquierda) hacia el este, donde indica flujo hacia la página, y (derecha) hacia el oeste, donde el punto rojo en el círculo indica flujo fuera de la página, para el hemisferio norte. La velocidad del paquete aéreo es u y la latitud es Φ. Crédito: W. Brune

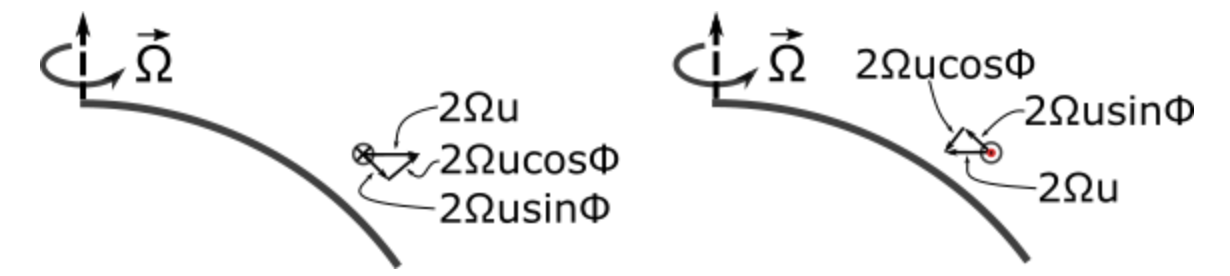
Podemos anotar las aceleraciones en las direcciones y y z debido a que el aire se mueve hacia el este con velocidad u:

Aceleración de Coriolis en la dirección y=\(\frac{D v}{D t}=-2 \Omega u \sin \phi\)

Aceleración de Coriolis en la dirección z=\(\frac{D w}{D t}=2 \Omega u \cos \phi\)

Flujo meridional (velocidad norte-sur)

¿Qué pasa con una paquetería aérea que viaja hacia el norte a una altitud constante? Tenga en cuenta que la parcela aérea que se mueve hacia el norte comienza a una mayor distancia del eje de la Tierra y se acerca más al eje de la Tierra si se mueve a la misma altura sobre la superficie. Su momento angular se conserva, por lo que se mueve más rápido hacia el este que la Tierra debajo de ella. En consecuencia, parece que se mueve hacia la derecha o hacia el este.

Si la misma parcela aérea se mueve hacia el sur a la misma altura sobre la superficie de la Tierra, entonces se mueve a una mayor distancia del eje de rotación de la Tierra. Su momento angular se vuelve menor que el de la Tierra, se ralentiza en relación con la Tierra, y se desvía hacia la derecha del sur o hacia el oeste.

Tanto en los casos de flujo zonal como meridional, la velocidad de la parcela aérea con respecto a la Tierra hace que la parcela aérea tenga un momento angular diferente al de la Tierra debajo de ella. La conservación del momento angular durante ese movimiento requiere que se agregue la fuerza aparente de Coriolis para describir el movimiento observado. Vea el video a continuación (2:11) para una explicación adicional:

Explicación de Coriolis

Haga clic aquí para ver la transcripción del video Explicación de Coriolis.

La fuerza Coriolis es una fuerza aparente que da cuenta del movimiento en una esfera giratoria, como la Tierra. Podemos romper la explicación de la fuerza de Coriolis en dos casos: flujo zonal, que es oriente oeste, y flujo meridional, que es norte sur. La explicación para ambos casos se basa en la conservación del momento angular. Para el flujo zonal, imagina una parcela aérea que se mueve hacia el este con velocidad, u. La aceleración angular es solo la velocidad angular cuadrada multiplicada por el radio de rotación. Si la parcela se mueve a una velocidad de u relativa a la superficie de la Tierra, entonces tiene algún momento angular extra, que es u dividido por r. Para encontrar la aceleración angular total que tiene la parcela aérea en movimiento, necesitamos cuadrar el momento angular de la parcela aérea, que es omega más u dividido por r, y luego multiplicarlo por r. Luego restamos la aceleración de la Tierra, que es solo omega al cuadrado r. La diferencia, a una buena aproximación, es 2 omega por u, que es solo la fuerza Coriolis, y, en el caso del movimiento hacia el este, se apunta lejos del eje de la Tierra en el hemisferio norte. Así, la fuerza Coriolis gira la parcela aérea hacia la derecha para flujo zonal. Si la parcela aérea se mueve hacia el oeste, entonces por el mismo argumento la fuerza Coriolis apunta hacia el eje de rotación de la Tierra en el hemisferio norte, que nuevamente gira la parcela aérea hacia la derecha. La explicación del flujo Meridional es más sencilla. Una parcela aérea inicialmente tiene el momento angular de la Tierra en su latitud. Si se mueve hacia el norte a la misma altura, entonces tiene más impulso angular que la Tierra debajo de ella. Y así va más rápido que la Tierra y parece moverse hacia la derecha. Si se mueve hacia el sur a la altura, entonces tiene menos impulso angular que la Tierra y parece disminuir la velocidad en relación con la Tierra y así parece moverse hacia la derecha.

Hallando la Magnitud y Dirección de la Fuerza Coriolis

La magnitud de la fuerza horizontal de Coriolis es simplemente\(2 \Omega|\vec{V}| \sin \varphi\), donde\(\varphi\) está la latitud. Esta magnitud se aplica tanto al hemisferio norte como al sur. La dirección de la fuerza de Coriolis es de 90 grados a la derecha del vector de velocidad horizontal en el hemisferio norte y 90 grados a la izquierda del vector de velocidad horizontal en el hemisferio sur.