10.6: Ecuaciones de Movimiento en Coordenadas Esféricas

Las tres variables utilizadas en las coordenadas esféricas son:

• longitud (denotada por\(λ\))
• latitud (denotada por\(φ\))
• distancia vertical (denotada por\(r\) desde el centro de la Tierra y por\(z\) desde la superficie de la Tierra, donde\(z = r – a\) y\(a\) es el radio de la Tierra)

Conversión entre coordenadas esféricas y cartesianas. Crédito: W. Brune

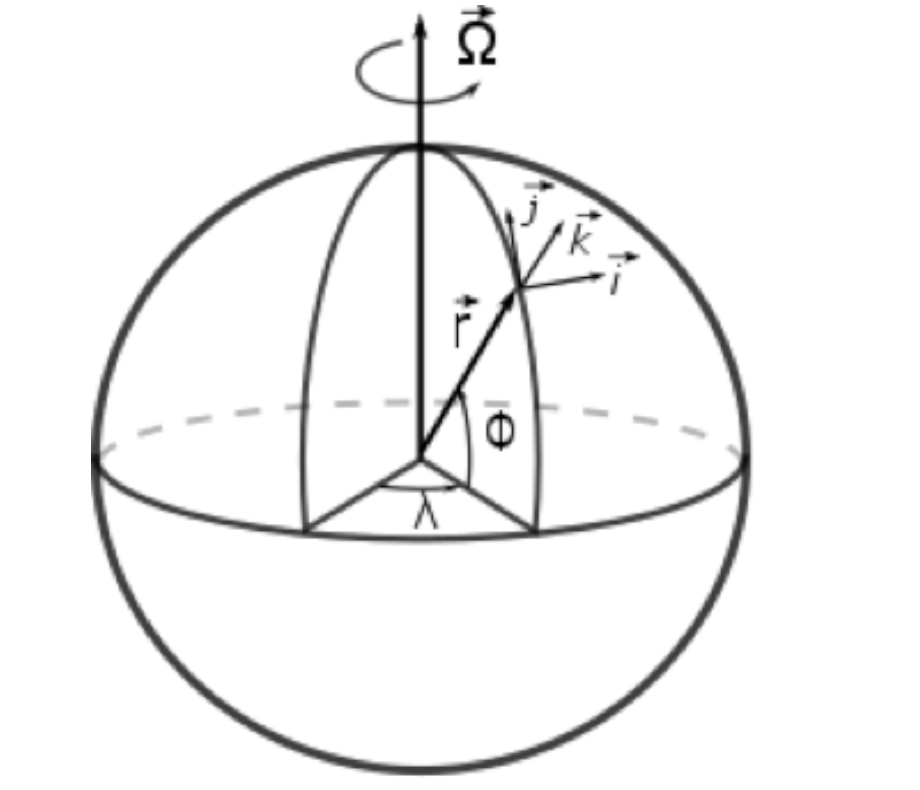
Tenga en cuenta que los vectores unitarios en coordenadas esféricas cambian con la posición. Por ejemplo, para una parcela aérea en el ecuador, el vector de unidad meridional\(\vec{j}\), es paralelo al eje de rotación de la Tierra, mientras que para una parcela aérea cerca de uno de los polos,\(\vec{j}\) es casi perpendicular al eje de rotación de la Tierra. En coordenadas esféricas, el vector de velocidad y sus componentes vienen dados por:

\[\vec{U}=u \vec{i}+v \vec{j}+w \vec{k}\]

\[u=r \cos \phi \frac{D \lambda}{D t}, \quad v=r \frac{D \phi}{D t}, \quad w=\frac{D z}{D t}\]

donde u, v y w son los componentes hacia el este, hacia el norte y hacia arriba de la velocidad, respectivamente. Estas velocidades se derivan de los cambios en las distancias hacia el este, hacia el norte y hacia arriba, que vienen dadas por:

\[d x=r \cos \phi d \lambda=\text { change in eastward distance } \cong a \cos \phi d \lambda\]

\[d y=r d \phi=\text { change in northward distance } \cong a d \phi\]

\[d z=d r=\text { change in upward distance }\]

Ahora escribamos la ecuación de conservación del momento promediado [10.16] en forma de componente en coordenadas esféricas. Simplemente te mostraremos cómo se realiza esta conversión sin realmente llevarte a través de todos los pasos. Tenga en cuenta que necesitamos tomar las derivadas totales de los vectores unitarios así como las velocidades:

\[\frac{D \vec{U}}{D t}=\frac{D}{D t}(\vec{i} u+\vec{j} v+\vec{k} w)=\vec{i} \frac{D u}{D t}+u \frac{D \vec{i}}{D t}+\vec{j} \frac{D v}{D t}+v \frac{\vec{D} \vec{j}}{D t}+\vec{k} \frac{D w}{D t}+w \frac{D \vec{k}}{D t}\]

Los términos que contienen derivados de los vectores unitarios se denominan “términos métricos”. Dependen de que la Tierra sea una esfera. En las coordenadas cartesianas, equivalen a cero.

Considere solo uno de estos términos métricos:

\[\frac{\vec{D} \vec{j}}{D t}=\frac{\partial \vec{j}}{\partial t}+u \frac{\partial \vec{j}}{\partial x}+v \frac{\partial \vec{j}}{\partial y}+w \frac{\partial \vec{j}}{\partial z}=0+u \frac{\partial \vec{j}}{\partial x}+v \frac{\partial \vec{j}}{\partial y}+0\]

Ya que para cualquier ubicación,\(\vec{j}\) es constante con el tiempo y\(\vec{j}\) no cambia en función de la altitud, eso deja\(\vec{j}\) dependiente únicamente de latitud y longitud. Mira\(\frac{\partial \vec{j}}{\partial y}\) primero. Establecer y = 0 en el ecuador, e y = a (radio de la Tierra) cerca del polo. Como se señaló anteriormente, en el ecuador,\(\vec{j}\) es paralelo al eje de rotación de la Tierra, pero cerca del polo, es casi perpendicular a él. Por lo tanto, el cambio en\(\vec{j}\) ir de sur a norte (aumentando y) debe estar apuntando hacia el centro de la Tierra y así\(\vec{j}\) cambia en −\(\vec{k}\) veces un pequeño cambio angular mientras y cambia por una vez lo mismo pequeño cambio angular. El resultado neto es que:

\[\frac{\partial \vec{j}}{\partial y}=\frac{-\vec{k}}{a}\]

Usando el mismo enfoque, podemos demostrar que:

\[\frac{\partial \vec{j}}{\partial x}=\frac{-\tan \phi}{a} \vec{i}\]

Las derivadas totales de los tres vectores unitarios son:

\[\frac{\vec{D} \vec{i}}{D t}=\frac{u}{a \cos \phi}(\vec{j} \sin \phi-\vec{k} \cos \phi)\]

\[\frac{\vec{D} \vec{j}}{D t}=-\frac{u \tan \phi}{a} \vec{i}-\frac{v}{a} \vec{k}\]

\[\frac{\vec{D} \vec{k}}{D t}=\frac{u}{a} \vec{i}+\frac{v}{a} \vec{j}\]

Armando todo esto:

\[\begin{aligned} \frac{D \vec{U}}{D t}=&\left(\frac{D u}{D t}-\frac{u v \tan \phi}{a}+\frac{u w}{a}\right) \vec{i}+\\ &\left(\frac{D v}{D t}+\frac{u^{2} \tan \phi}{a}+\frac{u w}{a}\right) \vec{j}+\\ &\left(\frac{D w}{D t}-\frac{u^{2}+v^{2}}{a}\right) \vec{k} \end{aligned}\]

Se puede hacer un análisis similar para los otros términos en la ecuación de impulso promediado.

Fuerza de Coriolis:

\[-2 \vec{\Omega} \times \vec{U}=2 \Omega(v \sin \phi-w \cos \phi) \vec{i}-(2 \Omega u \sin \phi) \vec{j}+(2 \Omega u \cos \phi) \vec{k}\]

Gravedad:

\[\vec{g}=-g \vec{k}\]

Fuerza de Gradiente de Presión (PGF):

\[-\frac{1}{\rho} \vec{\nabla} p=-\frac{1}{\rho} \frac{\partial p}{\partial x} \vec{i}-\frac{1}{\rho} \frac{\partial p}{\partial y} \vec{j}-\frac{1}{\rho} \frac{\partial p}{\partial z} \vec{k}\]

Fricción turbulenta (solo en la capa límite):

\[-\frac{C_{d}}{h}|\vec{V}| \vec{V}=-\frac{C_{d}}{h}|\vec{V}| u\left|u \vec{i}-\frac{C_{d}}{h}\right| \vec{V}|v| \vec{v} \vec{j}\]

Sumando todas las fuerzas, las ecuaciones de impulso promediadas en coordenadas esféricas en las direcciones zonal, meridional y vertical son, respectivamente:

\[\frac{D u}{D t}-\frac{u v \tan \phi}{a}+\frac{u w}{a}=-\frac{1}{\rho} \frac{\partial p}{\partial x}+2 \Omega v \sin \phi-2 \Omega w \cos \phi-\frac{C_{d}}{h}|\vec{V}| u\]

\[\frac{D v}{D t}-\frac{u^{2} \tan \phi}{a}+\frac{v w}{a}=-\frac{1}{\rho} \frac{\partial p}{\partial y}-2 \Omega u \sin \phi-\frac{C_{d}}{h}|\vec{V}| v\]

\[\frac{D w}{D t}-\frac{u^{2}+v^{2}}{a}=-\frac{1}{\rho} \frac{\partial p}{\partial z}-g+2 \Omega u \cos \phi\]