11.8: Así es como Reynolds hizo el promedio

Para cualquier variable, el valor observado puede escribirse como una suma del valor medio y un valor turbulento:

\[u=\bar{u}+u^{\prime}\]

donde\(\bar{u}\) es la media, o valor promedio, y\(u^{\prime}\) es la parte turbulenta.

El promedio se puede obtener promediando a\(u\) lo largo del tiempo o sobre el espacio o incluso haciendo un número de muestras y promediando sobre las muestras.

• promedio temporal:\[\bar{u}=\dfrac{\int u(t) d t}{\int d t}=\dfrac{\sum_{i=0}^{N-1} u\left(t_{i}\right)}{N}\]
• promedio espacial:\[\bar{u}=\dfrac{\int u(x) d x}{\int d x}=\dfrac{\sum_{i=0}^{N-1} u\left(x_{i}\right)}{N}\]

Si la turbulencia no cambia con el tiempo y es homogénea (es decir, la misma en todas las direcciones y para todos los tiempos), entonces estos promedios se igualan entre sí.

En la Lección 10, desarrollamos la ecuación del movimiento sin considerar realmente las variaciones a corto plazo y a pequeña escala, excepto para decir que llevaron a un arrastre turbulento, que actúa para resistir el flujo medio en la capa límite superior. Ahora queremos pensar en cómo capturar correctamente los efectos dinámicos del movimiento turbulento. Lo que queremos hacer es anotar las ecuaciones de movimiento que aprendiste en la Lección 10; sustituir las partes medias y turbulentas por las variables como u, v y w; promedio sobre todos los términos; y luego ver si podemos ordenar el términos para crear una ecuación para el viento medio y una ecuación para el viento turbulento. Este tipo de promediado se llama promedio de Reynolds.

Pero primero tenemos que aprender las reglas para promediar.

Reglas de promedio

c es constante; u y v son variables

\[\overline{u^{\prime}}=0\]

\[\overline{c u}=c \bar{u}\]

\[\overline{u+v}=\bar{u}+\bar{v}\]

\[\overline{(\bar{u} v)}=\bar{u} \bar{v}\]

\[\overline{\left(\frac{\partial u}{\partial t}\right)}=\frac{\partial \bar{u}}{\partial t}\]

Ahora vamos a aplicar estas reglas a una variable con una media y una parte turbulenta. Por ejemplo, considere el producto uv, que es solo la advección del viento horizontal en una dirección por el viento horizontal en la otra dirección.

Entonces, usando las reglas:

\[\begin{aligned} \overline{u v} &=\overline{\left(\bar{u}+u^{\prime}\right)\left(\bar{v}+v^{\prime}\right)} \\ &=\overline{\bar{u}} \bar{v}+\overline{\bar{u} v^{\prime}}+\overline{u^{\prime} \bar{v}}+\overline{u^{\prime} v^{\prime}} \end{aligned}\]

y

\[\overline{\overline{u v}}=\bar{u} \bar{v}\]

\[\overline{\bar{u} v^{\prime}}=\bar{u} \overline{v^{\prime}}=\bar{u} \cdot 0=0\]

\[\overline{u^{\prime} \bar{\nu}}=\overline{u^{\prime} \bar{\nu}}=0 \cdot \bar{\nu}=0\]

entonces

\[\overline{u v}=\bar{u} \bar{v}+\overline{u^{\prime} v^{\prime}}\]

¡Este segundo término, producto de dos términos turbulentos no es necesariamente cero! Mientras que el promedio de un término turbulento es cero por definición, el promedio de dos términos turbulentos no es necesariamente cero.

El siguiente video (3.11) describe adicionalmente el promedio de Reynolds:

Promedio de Reynold

Haga clic aquí para ver la transcripción del promedio de Reynold.

El promedio de Reynold es realmente bastante sencillo una vez que entiendes las reglas. Cada variable tiene un promedio y una perturbación, o turbulenta, parte. Tenemos que determinar el tiempo a lo largo del cual queremos encontrar el promedio. Pero después de hacer eso, podemos promediar todos los valores y luego restar el promedio de cada valor individual para encontrar la parte perturbada o turbulenta o fluctuante de ese valor. El promedio el valor promedio es, por supuesto, el mismo para todos los valores en la media. Utilizaré las palabras “media” y “promedio” indistintamente para el sustantivo que significa promedio. Y usaremos las palabras como perturbación, fluctuación y parte turbulenta para describir las variaciones de los valores individuales sobre el valor promedio. Las reglas son bastante simples. Primero, el promedio de un término perturbado o turbulento es 0, porque si no lo fuera, entonces el valor promedio sería incorrecto. En segundo lugar, el promedio del producto de una constante veces una variable es solo un producto del promedio de la constante multiplicado por el promedio de la variable. El promedio de la suma de dos variables es solo la suma del promedio de las dos variables. Y el promedio de un producto del valor promedio de una variable y otra variable es solo un producto de los promedios de las dos variables. Tenga en cuenta que el promedio de una variable es solo una constante. Ten cuidado. Pronto veremos que el promedio del producto de dos variables no es sólo el producto del promedio de dos variables. Finalmente, el promedio de la derivada de una variable es solo una derivada del promedio de la variable. Calculemos el promedio de Reynold de un término de la ecuación para la energía cinética, que es apenas 1/2 mv al cuadrado. Si dividimos por la densidad del aire, entonces tenemos la energía cinética cinemática. Cada término puede escribirse como su media en partes turbulentas. Veamos sólo el término u. Los términos v y w se pueden calcular de la misma manera. Entonces multiplicamos todos los términos, luego tomamos el promedio de Reynold y aplicamos las reglas. Los valores promedio de los valores promedio son solo valores promedio. Debido a que un valor promedio es una constante, obtenemos dos términos de una constante multiplicada por el promedio del término perturbado, que es apenas 0. Cuando terminamos, vemos que nos quedan dos términos: el promedio u cuadrado y el término de perturbación al cuadrado. Se puede hacer un modelo sencillo con un generador de números aleatorios para demostrar que el promedio del producto de dos términos de perturbación no es necesariamente 0. Este cálculo se eligió para que los promedios para u y v fueran 0. Y así el promedio del producto de promedio u y promedio v es 0, pero el promedio de las perturbaciones no es 0.

Ejemplo\(\PageIndex{1}\)

Considera dos números aleatorios que varían entre —0.5 y 0.5, llamados u y v. La siguiente figura muestra u, v, la media de uv y la media de u'v'. Por supuesto, la media de u'v' podría ser cero, pero no es necesariamente cero, como se muestra en esta figura.

Series temporales de dos variables aleatorias cuyas medias son cero (u en azul y v en rojo). La línea verde es el producto de la media de u y la media de v; este producto es igual a cero. La línea negra es la media del producto u'v'; ¡este producto no es cero! Crédito: W. Brune

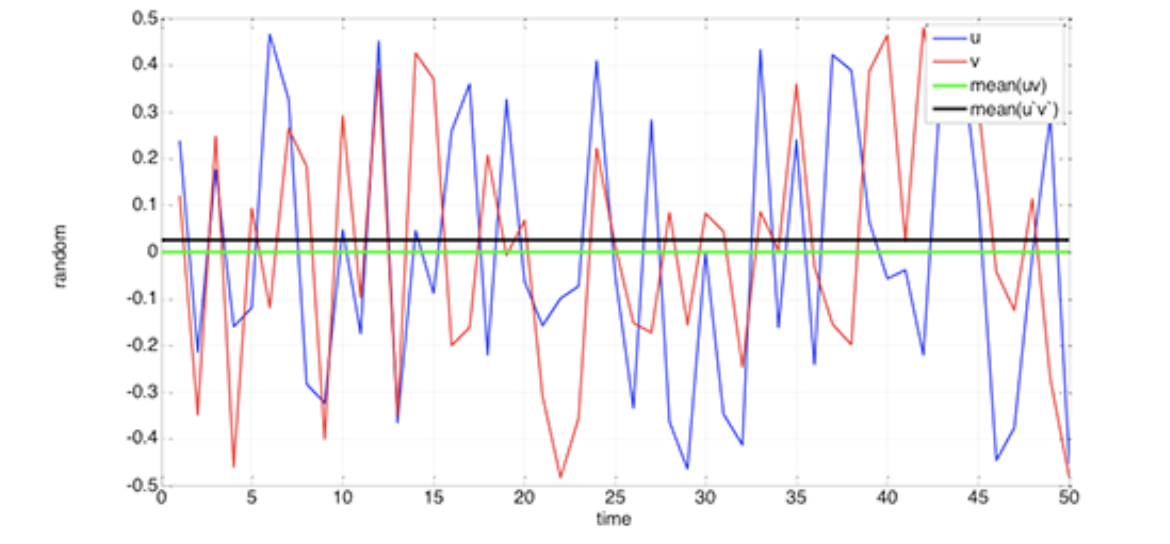
El mismo pensamiento se aplica a u ².

\[\overline{u^{2}}=\overline{\left(\bar{u}+u^{\prime}\right)\left(\bar{u}+u^{\prime}\right)}=\ldots=\bar{u}^{2}+\overline{u^{\prime 2}}\]

Recuerda tus estadísticas y el concepto de varianza:

\[\sigma_{u}^{2}=\frac{1}{N-1} \sum_{i=0}^{N-1}\left(u_{i}-\bar{u}\right)^{2} \approx \frac{1}{N} \sum_{i=0}^{N-1}\left(u_{i}-\bar{u}\right)^{2}=\frac{1}{N} \sum_{i=0}^{N-1}\left(u_{i}^{\prime}\right)^{2}=\overline{u^{2}}\]

Entonces, la varianza es la misma que el valor medio para el cuadrado de la parte turbulenta de la variable.

La covarianza de u y v viene dada por la ecuación:

covarianza\[(u, v)=\overline{u^{\prime} v^{\prime}}\]

Podemos tener una mejor idea de cuán grande es esta varianza dividiendo por el valor medio:

\[\mathrm{I}=\frac{\sigma_{u}}{\bar{u}}\]