7: Bases de la Circulación Impulsada por el Viento - Espiral y Transportes Ekman

En la Sección 6, se mencionó que las corrientes a gran escala en la superficie oceánica son todas impulsadas por el viento. Esto parece bastante lógico a primera vista, pero el explorador ártico Fridtjof Nansen notó algo extraño: los icebergs tienden a derivar en un ángulo a la derecha de la dirección predominante del viento. Para explicar esta notable observación, Ekman (1905) formuló una teoría que sigue siendo la piedra angular de la oceanografía física. El supuesto central es que cerca de la superficie oceánica, las mayores desviaciones del equilibrio geotrófico ocurren como resultado de la tensión del viento que conduce a la difusión de impulso en la dirección vertical. Esto significa que a una buena aproximación, las ecuaciones de balance de impulso horizontal\((1.2a)\) y\((1.2b)\) en la Sección 1 se convierten en:

\[\dfrac{\left(\dfrac{dp}{dx}\right)}{\rho}=f * v +K_v\dfrac{d^2u}{dz^2} \label{7.1a}\]

\[\dfrac{\left(\dfrac{dp}{dy}\right)}{\rho}=-f * u +K_v\dfrac{d^2v}{dz^2} \label{7.1b}\]

Ahora dividimos la velocidad en una parte geostrófica (\(u_g,v_g\)) y una velocidad Ekman ageostrófica (\(u_E,v_E\)):

\[\dfrac{\left(\dfrac{dp}{dx}\right)}{\rho}=f * (v_g+v_E) +K_v\dfrac{d^2(u_g+u_E)}{dz^2} \label{7.2a}\]

\[\dfrac{\left(\dfrac{dp}{dy}\right)}{\rho}=-f * (u_g+u_E) +K_v\dfrac{d^2(v_g+v_E)}{dz^2} \label{7.2b}\]

De las ecuaciones\((5.1a)\) y\((5.1b)\) en la Sección 5, podemos ver que las velocidades geastróficas se cancelan contra los términos del gradiente de presión en el lado izquierdo; los términos\(K_v\dfrac{d^2u_g}{dz^2}\) y se\(K_v\dfrac{d^2v_g}{dz^2}\) pueden descuidar. Por lo tanto, las ecuaciones simplifican para:

\[f * v_E =-K_v\dfrac{d^2 u_E}{dz^2} \label{7.3a}\]

\[f * u_E =K_v\dfrac{d^2 v_E}{dz^2} \label{7.3b}\]

que se puede reformular mediante la sustitución en una ecuación diferencial ordinaria de cuarto orden:

\[u_E =-\left(\dfrac{K_v}{f}\right)^2 \dfrac{d^4 u_E}{dz^4} \label{7.4}\]

con la solución (real):

\[u_E = A_1 \cos\left(\sqrt{\dfrac{f}{2K_v}}z+\phi_1\right)e^{\sqrt{\dfrac{f}{2K_v}}z}+A_2 \cos\left(\sqrt{\dfrac{f}{2K_v}}z+\phi_2\right)e^{-\sqrt{\dfrac{f}{2K_v}}z} \label{7.5}\]

Para determinar los diferentes coeficientes, utilizamos dos condiciones de límite:

1. El impacto directo del estrés del viento desaparece en las profundidades del océano:\(u_E \rightarrow 0\) para\(z \rightarrow -\infty\). Por lo tanto,\(A_2\) debe ser igual a\(0\).
2. En la Sección 6, argumentamos que cerca de la interfaz océano-atmósfera, la tensión del viento es linealmente proporcional al gradiente de velocidad vertical; esto significa que si el viento sopla en la dirección zonal (Oeste-Este),\(\dfrac{du_E}{dz}=\dfrac{\tau_w}{\rho K_v}\) (ecuación\(6.1\)),\(\dfrac{dv_E}{dz}=0\) para\(z=0\). Esto lleva a\(\phi_1=-\dfrac{\pi}{4}\),\(A_1=\dfrac{\tau_w}{\rho \sqrt{f K_v}}\).

En general, contamos con:

\[u_E = \dfrac{\tau_w}{\rho \sqrt{f K_v}} \cos\left(\sqrt{\dfrac{f}{2K_v}}z-\dfrac{\pi}{4}\right)e^{\sqrt{\dfrac{f}{2K_v}}z} \label{7.6a}\]

\[v_E = -\dfrac{K_v}{f}\dfrac{d^2 u_E}{dz^2}=\dfrac{\tau_w}{\rho \sqrt{f K_v}} \sin\left(\sqrt{\dfrac{f}{2K_v}}z-\dfrac{\pi}{4}\right)e^{\sqrt{\dfrac{f}{2K_v}}z} \label{7.6b}\]

Los transportes Ekman por unidad de área en las direcciones zonal y meridional son respectivamente:

\[M_{E,x}=\rho\int_{-\infty}^0 u_E\, dz\]

\[M_{E,y}=\rho\int_{-\infty}^0 v_E\, dz\]

Estos podrían calcularse integrando Ecuaciones\(\ref{7.6a}\) y\(\ref{7.6b}\), pero es mucho más fácil usar Ecuaciones\(\ref{7.3a}\) y\(\ref{7.3b}\):

\[\begin{align} M_{E,x} &=\dfrac{K_v \rho}{f}\int_{-\infty}^0 \dfrac{d^2 v_E}{dz^2}\, dz \\[4pt] &=\dfrac{K_v \rho}{f}\left(\dfrac{dv_E}{dz}(z=0)-\dfrac{dv_E}{dz}(z\rightarrow-\infty)\right) \\[4pt] &=0 \label{7.7a} \end{align}\]

y

\[\begin{align} M_{E,y} &=-\dfrac{K_v \rho}{f}\int_{-\infty}^0 \dfrac{d^2 u_E}{dz^2}\, dz \\[4pt] &=-\dfrac{K_v \rho}{f}\left(\dfrac{du_E}{dz}(z=0)-\dfrac{du_E}{dz}(z\rightarrow-\infty)\right) \\[4pt] &=-\dfrac{\tau_w}{f} \label{7.7b} \end{align}\]

¿Qué significa todo esto? En la superficie del océano,

\[u_E=\dfrac{\tau_w}{\rho \sqrt{2f K_v}} \nonumber\]

y

\[v_E=-\dfrac{\tau_w}{\rho \sqrt{2f K_v}} \nonumber\]

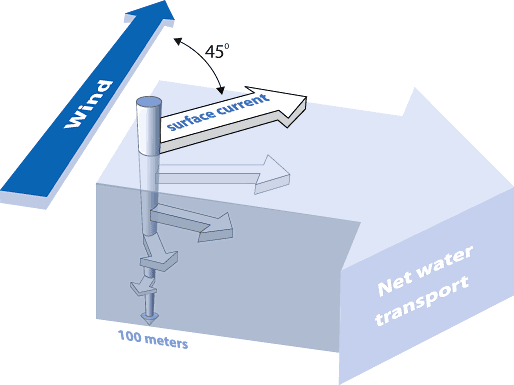
vía Ecuaciones\ ref {7.6a} y\ ref {7.6b}, es decir, la velocidad de Ekman está en un ángulo de\(45^{\circ}\) a la derecha de la dirección del viento en el hemisferio norte (y a la izquierda del viento en el hemisferio sur) debido a la fuerza de Coriolis. Profundizando, la fuerza de Coriolis sigue girando la dirección del flujo más hacia la derecha, mientras que la velocidad del agua disminuye exponencialmente con la profundidad. Como se ilustra en la Figura siguiente (cortesía de NOAA), el patrón de flujo general forma una llamada espiral Ekman. Además, Ecuación\(\ref{7.7a}\) e\(\ref{7.7b}\) implican que el transporte neto de Ekman se encuentra\(90^{\circ}\) a la derecha de la dirección del viento en el hemisferio norte.