5.4: Energía en flujo de canal abierto

Para abordar los dos problemas de transición de canal planteados anteriormente, necesitamos tener una mirada más cercana a la energía mecánica en un flujo de canal abierto, y cómo se cambia la partición de los diversos componentes de esa energía mecánica, cinética y potencial, en la transición en cuestión.

Señalé en el capítulo 3 que la ecuación de Bernoulli es una expresión del teorema trabajo-energía: el trabajo realizado por la presión del fluido es igual al cambio en la energía cinética del flujo. Recuerde que, en casos como este, si el cambio en la energía cinética es reversible una cantidad llamada energía potencial se define como menos el trabajo realizado, y entonces la suma de energía cinética y energía potencial, a menudo llamada energía mecánica, queda inalterada o conservada. Se dice que las fuerzas para las que esto es cierto, como la presión del fluido en este caso, son fuerzas conservadoras. La gravedad es un buen ejemplo: una pelota lanzada hacia arriba gana energía potencial al subir al mismo ritmo que pierde energía cinética, si se ignora la resistencia friccional del aire. Las fuerzas de fricción, por otro lado, degradan la energía mecánica en energía térmica (más comúnmente llamada energía térmica o térmica).

Revise la derivación de la ecuación de Bernoulli en el Capítulo 3 y verá que la presión del fluido es una fuerza conservadora: en ausencia de fricción, el cambio en la energía potencial de presión por unidad de volumen entre dos puntos\(1\) y\(2\) hacia abajo de una línea aerodinámica, que es menos el trabajo per volumen unitario\(- (p_{2} - p_{1})\) por la presión del fluido, es igual al cambio en la energía cinética por unidad de volumen\((\rho/2)({v_{2}}^{2}- {v_{1}}^{2})\), por lo que los dos tipos de energía mecánica son intercambiables en este caso también. Por lo tanto, debería parecer natural que cuando el fluido está en un campo de gravedad, también se pueda incluir un término para energía potencial gravitacional en la ecuación de Bernoulli. Debido a que la energía potencial gravitacional es\(mgh\) (donde m es la masa del cuerpo bajo consideración y\(h\) es la elevación relativa a un plano horizontal arbitrario), la energía potencial por unidad de volumen es\(\rho gh\).

Entonces, en la ecuación ampliada de Bernoulli la energía mecánica por unidad de volumen de fluido que se mueve a lo largo de una línea aerodinámica\(v^{2} / 2+p+\rho g h\),, es constante. Esto se puede escribir un poco más convenientemente para nuestros propósitos como energía por unidad de peso de fluido\(E_{w}\). Porque el peso es igual al volumen multiplicado por\(\rho g\),

\[E_{W}=\frac{v^{2}}{2 g}+\frac{p}{\gamma}+h \label{5.3} \]

Obsérvese que cada término tiene las dimensiones de longitud;\(E_{w}\) se llama cabeza total, y los términos de la derecha se denominan cabeza de velocidad, cabeza de presión y cabeza de elevación, respectivamente. En un fluido real, la fricción degrada la energía mecánica para calentar a medida que el fluido se mueve a lo largo de una línea Esta disminución en la energía mecánica de punto a punto, expresada por unidad de peso de fluido, se denomina pérdida de cabeza. Si suma los tres términos a la derecha en la Ecuación\ ref {5.3} la suma disminuye aguas abajo, sin importar cómo cambien los valores de los términos individuales.

Sería bueno generalizar la Ecuación\ ref {5.3} para que se aplique a todo un flujo de canal abierto, no solo a cada aerodinámica en él. El problema al hacer esto es que la velocidad, la elevación y la presión no son constantes de un punto a otro en una sección transversal. Pero si no hay fuertes aceleraciones de fluidos normales a la dirección del flujo, la presión está cerca de distribuirse hidrostáticamente:\(p=\gamma(d-y)\). Luego se puede escribir la suma del cabezal de elevación y el cabezal de presión

\(\begin{aligned} h+\frac{p}{\gamma} &=h_{\mathrm{o}}+y+\frac{p}{\gamma} \\ &=h_{\mathrm{o}}+y+\frac{\gamma(d-y)}{\gamma} \end{aligned}\)

\[=h_{\mathrm{o}}+d \label{5.4} \]

donde\(h_{\text{o}}\) está la elevación de la parte inferior del canal. Las variaciones de presión y elevación sobre la sección transversal se toman en cuenta así en la Ecuación\ ref {5.3}. La variación en la velocidad sigue siendo un problema, pero en flujos turbulentos el perfil de velocidad es tan plano en la mayor parte de la sección que solo se necesita hacer una pequeña corrección para reemplazar\(v\) por la velocidad media de la sección transversal\(U\). La ecuación\ ref {5.3} se puede escribir entre dos secciones transversales\(1\) y\(2\) en un flujo de canal que varía solo lentamente aguas abajo como

\(\text{head loss} =\left(E_{w}\right)_{2}-\left(E_{w}\right)_{1}\)

\[=\frac{U_{2}^{2}}{2 g}+h_{\text{o}2}+d_{2}-\left(\frac{U_{1}^{2}}{2 g}+h_{\text{o}1}+d_{1}\right) \label{5.5} \]

Una gráfica de\(E_{w}\) contra posición de canal descendente se denomina línea de grado de energía, y la pendiente de esta línea (o, generalmente, curva) es el gradiente de energía o pendiente de energía.

En un flujo uniforme de canal abierto, para el cual tanto la energía cinética como la energía potencial son las mismas en cada sección transversal pero la energía potencial disminuye aguas abajo, la pérdida de carga es simplemente la tasa de disminución de la altura de elevación aguas abajo, o en otras palabras, la pendiente de la superficie del agua y el lecho superficie, que entonces también es igual a la pendiente de energía.

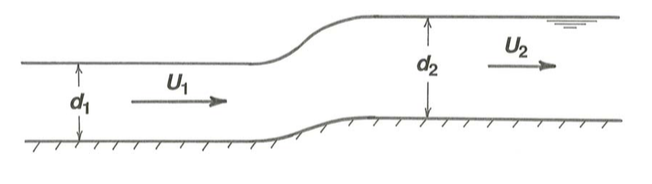
A menudo es útil aplicar la Ecuación\ ref {5.5} a un flujo de canal abierto que varía lo suficientemente rápido como para que haya poca pérdida de carga pero lo suficientemente lenta como para que la aproximación hidrostática-presión no sea demasiado incorrecta. Esas condiciones no son muy restrictivas: ejemplos son un suave ascenso o caída en el lecho del canal, como en el primer “problema práctico” planteado anteriormente en este capítulo (Figura 5.2.1) o una suave expansión o contracción de las paredes del canal. El desarrollo en el resto de esta sección está destinado a atender este tipo de casos. La ecuación\ ref {5.5} se convierte

\[\frac{U_{2}^{2}}{2 g}+h_{\text{o}2}+d_{2}=\frac{U_{1}^{2}}{2 g}+h_{\text{o}1}+d_{1} \label{5.6} \]

Una cantidad conveniente para sustituir en la Ecuación\ ref {5.6} es\(d+U^{2} / 2 \mathrm{g}\), llamada la cabeza específica\(H_{\text{o}}\):

\[H_{\mathrm{o}}=d+\frac{U^{2}}{2 g} \label{5.7} \]

Ho, también llamada la energía específica, es simplemente la cabeza (es decir, energía de flujo por unidad de peso) en relación con el fondo del canal. Usando\(H_{\text{o}}\), la ecuación\ ref {5.6} se convierte

\[H_{\mathrm{o} 2}+h_{\mathrm{o} 2}=H_{\mathrm{o} 1}+h_{\mathrm{o} 1} \label{5.8} \]

o

\[H_{\mathrm{o} 2}=H_{\mathrm{o} 1}-\left(h_{\mathrm{o} 2}-h_{\mathrm{o} 1}\right) \label{5.9} \]

Ahora mire una porción unitaria paralela a la dirección del flujo en un flujo bidimensional. En otras palabras, no hay que preocuparse por los flancos porque están muy lejos en relación con lo que está sucediendo localmente). La descarga por unidad de ancho\(q\) es constante e igual a\(Ud\). La sustitución de\(U = q/d\) en la definición de cabeza específica elimina\(U\) y proporciona una relación entre\(d\) y\(H_{\text{o}}\) para cada valor de\(q\):

\[H_{\mathrm{o}}=\frac{q^{2}}{2 g d^{2}}+d \label{5.10} \]

La familia de curvas de\(H_{\text{o}}\) vs\(d\) para varios valores de\(q\) se denomina diagrama de cabeza específica o diagrama de energía específica (Figura\(\PageIndex{1}\)).

Figura\(\PageIndex{1}\): El diagrama específico de energía. Cada una de las curvas es para un valor dado de descarga por unidad de ancho,\(q\).

Figura\(\PageIndex{2}\): El diagrama específico de energía para un valor particular de\(q\), para ilustrar el efecto de elevar el fondo del canal por una distancia\(\delta h\). Ver texto para explicación.

Para ilustrar la utilidad del diagrama específico de cabeza, supongamos que el flujo que se aproxima al paso mostrado en la Figura 5.2.1 se caracteriza por valores de\(q\)\(d\), y\(H_{\text{o}}\) (es decir: descarga por unidad de ancho de canal; profundidad; y energía de flujo) que representan en el punto\(\text{P}_{1}\) en Figura\(\PageIndex{2}\), en la parte superior de la curva para el dado\(q\). Debido a que el fondo se eleva por una distancia positiva\(\delta h = h_{\text{o}2} - h_{\text{o}1}\), por la Ecuación\ ref {5.9} la cabeza específica\(H_{\text{o}2}\) asociada con el flujo aguas abajo de la transición se encuentra una distancia\(\delta h\) a la izquierda de a\(H_{\text{o}1}\) lo largo del\(H_{\text{o}1}\) eje;\(\text{P}_{2}\) es el punto correspondiente que representa el flujo. Por lo tanto, la profundidad de flujo aguas abajo del escalón es menor\((\Delta d)_{P}\) en la Figura\(\PageIndex{2}\) que en el flujo que se aproxima, y por\(q = Ud\) la relación la velocidad del flujo es mayor (Figura\(\PageIndex{3}\)). ¿Eso daña tu intuición?

En virtud de la forma doblemente ramificada de las curvas de la Figura también puede\(\PageIndex{1}\) haber un flujo que se aproxima, representado por punto\(Q_{1}\) en la parte inferior de la misma curva, con exactamente la misma descarga y energía de flujo pero con menor profundidad y mayor velocidad. En este caso el flujo aguas abajo de la transición, representado por el punto\(Q_{2}\) encontrado al mover una distancia\(\delta h\) hacia la izquierda a lo largo del\(H_{\text{o}}\) eje como antes, tiene una profundidad\((\delta d)Q\) mayor por que el flujo que se aproxima, y menor velocidad (Figura\(\PageIndex{4}\)). Los hidráulicos de canal abierto hablan de profundidades alternas superiores e inferiores.

Figura\(\PageIndex{3}\): Efecto de elevar el fondo del canal por debajo de un flujo subcrítico que se aproxima. La profundidad disminuye a lo largo de la transición y la velocidad media del flujo aumenta.

Figura\(\PageIndex{4}\): Efecto de elevar el fondo del canal por debajo de un flujo supercrítico que se aproxima. La profundidad aumenta a lo largo de la transición y la velocidad media del flujo disminuye.

Para los puntos en los que las curvas de\(d\) vs\(H_{\text{o}}\) tienen tangentes verticales, la profundidad y la velocidad no cambian en la transición. Los flujos correspondientes a estos puntos se denominan flujos críticos. La ecuación para tales puntos se encuentra en dos pasos. Primero, diferenciar la función en la Ecuación\ ref {5.10} para encontrar\(d H_{\mathrm{o}} / d(d)\), establecer esta derivada igual a cero, y resolver para\(q\) como una función de\(d\). El resultado es

\[q_{c}^{2}=g d_{c}^{3} \label{5.11} \]

donde el subíndice\(c\) indica que la ecuación es para la condición crítica de tangencia vertical. Luego sustituya esta expresión por\(q_{c}^{2}\) en la Ecuación\ ref {5.10} para obtener

\[H_{\mathrm{oc}}=\frac{3}{2} d_{c} \label{5.12} \]

nuevamente con el subíndice\(c\) denotando flujo crítico.

El lugar de puntos en el diagrama específico de cabeza para el que el flujo es crítico es, por lo tanto, una línea recta con una pendiente de\(2/3\). Se muestra en la Figura\(\PageIndex{1}\) como una línea discontinua que se extiende hacia arriba y hacia la derecha desde el origen. Los flujos correspondientes a puntos por encima de la línea son subcríticos (profundidades más profundas y velocidades más bajas), y los flujos correspondientes a puntos por debajo de la línea son supercríticos (profundidades menos profundas y velocidades más altas).

Así, a cada combinación de descarga por unidad de ancho\(q\) y energía de flujo (representada por\(H_{\text{o}}\)) corresponden dos estados de flujo diferentes posibles, con diferente profundidad y velocidad dadas por las dos intersecciones de la curva de\(d\) vs\(H_{\text{o}}\) para eso\(q\) y la vertical línea asociada con eso\(H_{\text{o}}\). En algunos tipos de transiciones a lo largo del canal, el flujo es forzado desde uno de estos estados al otro, pasando así por el estado crítico durante la transición. Cualquier flujo, sea cual sea su origen y por lo tanto sea cual sea su profundidad y descarga, cae en algún momento en una de las curvas del diagrama específico de cabeza, y por lo tanto es supercrítico o subcrítico (o crítico). El comportamiento de ese flujo en una transición es radicalmente diferente dependiendo de si el flujo es subcrítico o supercrítico. Esta diferencia de comportamiento es fundamentalmente una consecuencia del requerimiento de conservación de la energía de flujo expresado por la Ecuación\ ref {5.6}, junto con el requisito de conservación de masa que

\[q=\frac{U_{1}}{d_{1}}=\frac{U_{2}}{d_{2}} \label{5.13} \]

Por ejemplo, en la transición examinada anteriormente, las variables\(U_{1}\),\(d_{1}\),\(h_{\text{o}1}\), y\(h_{\text{o}2}\) se dan todas, y las Ecuaciones\ ref {5.6} y\ ref {5.12} luego especifican exactamente qué combinación de\(U_{2}\) y\(d_{2}\) debe contener.

Ocurre que la condición para el flujo crítico corresponde a un número de unidad de\(U /(g d)^{1 / 2}\) Froude de flujo medio. Para verificar esto, simplemente sustituya la Ecuación\ ref {5.11}, la condición para el flujo crítico, en la Ecuación\ ref {5.7}, la definición para\(H_{\text{o}}\), para obtener una relación entre\(U\) y\(d\) para flujo crítico:\(U^{2} = gd\), o\(\mathrm{Fr}=1\). Los flujos subcríticos se caracterizan por números de Froude menores a uno, y los flujos supercríticos se caracterizan por números de Froude mayores a uno.

Verás en el Capítulo 6, sobre el flujo oscilatorio, que es la velocidad c de una ola de gravedad en aguas poco profundas\((g d)^{1 / 2}\), dónde\(d\) está la profundidad del agua. Si sustituyes esta velocidad de onda\(c\) por el denominador\((g d)^{1 / 2}\) en la definición del número de Froude, ves que para un número de Froude igual a uno la velocidad de flujo media es igual a la velocidad de las ondas superficiales. Una ola de la superficie del agua que se mueve en la dirección aguas arriba parece a un observador en la orilla del canal estar quieta. Esto significa que si el número de Froude del flujo es mayor que uno, las perturbaciones en forma de onda no pueden propagarse aguas arriba: el flujo que viene de aguas arriba no puede saber lo que le espera en las posiciones aguas abajo. En el flujo subcrítico, por otro lado, el flujo aguas arriba puede ser influenciado, comúnmente para largas distancias, por condiciones aguas abajo.

Ese último punto queda bien ilustrado por una consideración final del escalón ascendente mostrado en la Figura 5.2.1. A medida que la altura del escalón se incrementa gradualmente, el punto correspondiente en la rama superior del diagrama de cabeza específico se mueve hacia la izquierda y hacia abajo desde el punto\(\text{P}\) hacia el punto de tangente vertical,\(\text{C}\). Cuanto más a lo largo de la curva se desplaza el punto, mayor es la disminución de la profundidad de flujo sobre el escalón. Pero hay un límite a este efecto: la energía específica no puede disminuir más allá de la correspondiente al punto\(\text{C}\) de tangente vertical, porque el flujo tiene que permanecer en el\(q = \text{constant curve}\). Entonces, ¿qué sucede a medida que el paso se eleva aún más? El flujo sobre el escalón sigue siendo crítico y la profundidad aguas arriba del escalón aumenta. En lugar de no tener ningún efecto sobre el flujo aguas arriba, como fue el caso de los escalones más bajos, el escalón ahora actúa como presa: su efecto se siente muy aguas arriba.

Quizás se esté preguntando en este punto cómo se puede lograr la condición de flujo representada por el punto alternativo en el diagrama de cabeza específica. Para ver cómo podría suceder eso, supongamos que la geometría del escalón en la Figura 5.2.1 se cambia un poco: después de alcanzar la cresta del escalón, el fondo del canal vuelve a caer suavemente a su altura original. Si ahora para el flujo subcrítico que se aproxima con dada\(q\) la altura del escalón se eleva hasta el punto donde el flujo sobre el escalón acaba de alcanzar la condición crítica, representada por el punto\(\text{C}\) en la curva para lo dado\(q\) en la Figura\(\PageIndex{5}\), el paso del flujo aguas abajo a la nivel original se manifiesta en el diagrama específico de cabeza como un cambio de punto\(\text{P}\) a punto\(\text{Q}\) verticalmente por debajo del punto original\(\text{P}\) pero en la extremidad inferior (supercrítica) de la\(q\) curva. El flujo se encuentra ahora en la misma elevación, y tiene la misma energía (es decir, la misma elevación canal-fondo y la misma altura específica), pero ahora fluye a una combinación muy diferente de profundidad y velocidad, correspondiente al flujo supercrítico (Figura\(\PageIndex{6}\)). Lo que está sucediendo, físicamente, en contraste con lo gráfico, es que el flujo crítico en la cresta del escalón se acelera hacia abajo por el lado sotento del escalón, para alcanzar una velocidad supercrítica (y, en virtud de la conservación de la masa, una profundidad menos profunda). Si el escalón se eleva incluso más allá de lo necesario para alcanzar la condición crítica, entonces el flujo aguas arriba es embalado, y su profundidad aumenta, forzando el punto\(\text{P}\) hacia arriba a la derecha a lo largo de la curva para lo dado\(q\) en el diagrama específico de energía.

Figura\(\PageIndex{5}\): El diagrama específico de energía para un valor particular de q, para ilustrar el efecto de subir y luego bajar el fondo del canal para forzar el paso del flujo de subcrítico a supercrítico.

Figura\(\PageIndex{6}\): El comportamiento del flujo sobre una subida y luego una caída del fondo del canal, cuando un flujo subcrítico que se aproxima es forzado a la condición crítica elevando el escalón en un incremento suficientemente grande.

Un comentario final es que el flujo supercrítico aguas abajo del escalón no permanece supercrítico por una distancia muy grande, a menos que la pendiente del fondo aguas abajo del escalón se vuelva mucho más pronunciada. Si el fondo conserva su suave pendiente, es probable que se forme un salto hidráulico en algún punto aguas abajo, con la consecuencia de que el flujo revierte a su condición subcrítica original; ver la siguiente sección.