7.2: El efecto Coriolis en la superficie terrestre

Los flujos de fluidos que observas en la superficie de la Tierra experimentan una aceleración de Coriolis. Eso es porque la Tierra está rotando, y tanto tú como el fluido que fluye están rotando con ella. Los efectos que descubriste en tu tocadiscos también aparecen en esos flujos. Los únicos lugares que esto debería parecerle realmente obvio son en el Polo Norte y el Polo Sur, donde la superficie de la Tierra es perpendicular al eje de rotación. Pero la aceleración de Coriolis afecta también a los movimientos fluidos en todas partes de la superficie de la Tierra.

El desarrollo matemático completo del efecto Coriolis, aunque sencillo, nos alejaría demasiado del camino de estas notas, así que te daré una imagen abreviada e incompleta, solo por el sabor.

Mencioné anteriormente que la velocidad de rotación de un cuerpo giratorio se denota por\(\omega\). Pero para ser específicos sobre tal rotación, es necesario describir la orientación y el sentido de la rotación también. La rotación de la Tierra se describe por su velocidad angular, un vector, denotado por \(\Omega\), que se encuentra dentro del eje de rotación y con una longitud igual a la velocidad de rotación\(\omega\). Por convención, el vector de velocidad angular apunta hacia el norte para expresar el sentido de rotación de la Tierra, que es en sentido antihorario cuando se ve desde arriba del Polo Norte (Figura\(\PageIndex{1}\)). La velocidad angular especifica \(\Omega\)así la orientación, el sentido y la velocidad de rotación de la Tierra.

Figura\(\PageIndex{1}\): El vector de velocidad angular de la Tierra giratoria.

Mira un punto en la superficie de la Tierra. La velocidad\(v\) de ese punto, relativa al espacio exterior, es igual a la velocidad angular\(\omega\) multiplicada por la distancia desde el eje de rotación hasta el punto. Expresado en términos del radio\(R\) de la Tierra y el ángulo de latitud\(\phi\), esto se puede escribir\(R \omega \sin \left(90^{\circ}-\phi\right)\) (Figura\(\PageIndex{2}\)).

Figura\(\PageIndex{2}\): Esbozo de definición para escribir la velocidad de un punto dentro o sobre la Tierra en términos del radio de la Tierra, la velocidad angular de la Tierra y la latitud del punto.

Una manera más elegante de observar el movimiento de un punto en la superficie terrestre es caracterizar la posición del punto por un vector de posición \(r\)que se extiende desde el centro de la Tierra hasta el punto dado (Figura\(\PageIndex{3}\)) y luego expresar la velocidad del punto como\(\boldsymbol{v}=\boldsymbol{\Omega} \times \boldsymbol{r}\). El producto del lado derecho es un producto cruzado de vectores, definido de manera que el resultado tenga una magnitud\(r \omega \sin \left(90^{\circ}-\phi\right)\), que es lo mismo que el resultado en el último párrafo, porque\(r = R\). Tenga en cuenta que el producto vectorial es en sí mismo un vector; el producto vectorial está dispuesto de manera que su dirección y sentido describan correctamente la velocidad del punto dado en la superficie de la Tierra. Tenga en cuenta también que \(v\)es normal a ambos \(\Omega\)y \(r\); esa es una de las propiedades del producto cruzado.

Figura\(\PageIndex{3}\): Otra forma de expresar la velocidad de un punto dentro o sobre la Tierra.

Ahora mira una pequeña partícula marcadora que se mueve junto con el aire de la atmósfera o el agua del océano. Esa partícula tiene su propia velocidad relativa a la Tierra sólida; llame a esa velocidad \(v_{R}\), donde el subíndice\(R\) está destinado a sugerir que la velocidad es relativa a la Tierra giratoria. El movimiento de la partícula también se puede ver desde el espacio exterior; llamar a su velocidad relativa a ese marco de referencia “fijo” \(v_{I}\), donde el subíndice\(I\) significa inercial, adjetivo que en la física se asocia a un marco de referencia que no se está acelerando. Debería tener sentido para ti que

\[\boldsymbol{v}_{\boldsymbol{I}}=\boldsymbol{v}_{\boldsymbol{R}}+\boldsymbol{\Omega} \times \boldsymbol{r} \label{7.1} \]

La ecuación\ ref {7.1} simplemente te dice que la velocidad absoluta de la partícula en movimiento es la suma de su velocidad relativa a la Tierra giratoria más la velocidad de rotación del punto, estacionaria respecto a la Tierra, más allá de la cual la partícula pasa a estar moviéndose en un momento dado.

Las complicaciones comienzan cuando observamos la aceleración de la partícula marcadora, no solo su velocidad. La aceleración de la partícula es la tasa temporal de cambio de su velocidad. Para encontrar la aceleración hay que diferenciar el vector \(v_{I}\)con respecto al tiempo, y luego, para usar el resultado en nuestro marco de referencia terrenal giratorio, expresar el resultado en términos de cantidades como las \(v_{R}\)que se observan desde dentro de ese marco giratorio de referencia. Simplemente citaré el resultado para \(a_{I}\), la aceleración de la partícula en relación con el marco de referencia del espacio exterior:

\[\boldsymbol{a_{I}} = \boldsymbol{a_{R}}+2 \boldsymbol{\Omega} \times \boldsymbol{v_{R}}+ \boldsymbol{\Omega} \times \boldsymbol{\Omega} \times \boldsymbol{r}+\frac{d \boldsymbol{\Omega}}{d t} \times \boldsymbol{r} \label{7.2} \]

donde \(a_{R}\)está la aceleración de la partícula tal como se observa desde la Tierra giratoria. (Para más detalles, véase Pedlosky, 1987, Capítulo 1.)

Hay cuatro términos en el lado derecho de la Ecuación\ ref {7.2}. El primero, \(a_{R}\), es fácil de entender, pero los otros tres necesitan alguna explicación. El cuarto expresa el efecto de la tasa temporal de cambio de la velocidad de rotación; es algo de lo que no debemos preocuparnos para los flujos geofísicos. El tercero es la aceleración centrípeta, con la que todos ustedes están familiarizados al menos de manera cualitativa: si atan una cuerda alrededor de una roca y la balancean en un círculo grande, están produciendo una aceleración centrípeta (“búsqueda central”) de la roca, que surge del radial dirigido hacia adentro fuerza que estás ejerciendo sobre la roca para limitarla a viajar en un arco circular en lugar de salir recto por sí sola. El segundo término es el que buscamos en este ejercicio: es la aceleración de Coriolis.

Observe más de cerca el término de aceleración de Coriolis en la Ecuación\ ref {7.2}. En primer lugar, es un vector en sí, porque es un producto cruzado de dos vectores. Su magnitud es una función lineal de la magnitud de la velocidad \(v_{R}\): cuanto más rápido se mueve la partícula, mayor es la aceleración de Coriolis. Además, su magnitud depende no sólo de la magnitud de \(v_{R}\)sino también de la dirección de \(v_{R}\)relativo al eje de la Tierra. En todos los casos, sin embargo, la dirección de la aceleración de Coriolis es normal a la propia vR (recuerde las propiedades del producto cruzado), y eso es consistente con lo que aprendió sobre la aceleración de Coriolis en su gran plataforma giratoria.

Una buena manera de estudiar los efectos de la aceleración de Coriolis en los fluidos que se mueven en la superficie de la Tierra es observar un punto particular de la superficie de la Tierra a una latitud particular\(\phi\) (Figura\(\PageIndex{4}\)). Para un observador local la situación allí se ve plana, así que piensa en un plano que sea tangente a la superficie de la Tierra en el punto dado. Voy a llamar a eso el plano horizontal, porque es horizontal en el punto tangente. Los movimientos tanto de la atmósfera como de los océanos más afectados por la aceleración de Coriolis son flujos casi completamente horizontales: los movimientos verticales a gran escala en la atmósfera y los océanos suelen ser de una velocidad mucho menor que los movimientos horizontales, y movimientos verticales localmente fuertes, como dentro de la convección de nubes células, están en escalas de espacio y tiempo para las cuales el efecto Coriolis resulta poco importante.

Figura\(\PageIndex{4}\): El plano tangente “horizontal”.

En el plano horizontal es natural establecer un sistema de coordenadas con un eje vertical, uno en la dirección de movimiento de la partícula, y el otro horizontal y normal a la dirección del movimiento (Figura\(\PageIndex{5}\)). Y la propia aceleración de Coriolis puede resolverse en componentes en esas tres direcciones (Figura\(\PageIndex{6}\)). Piense solo en los componentes horizontales de la aceleración de Coriolis, porque son lo que son importantes para los movimientos horizontales de los fluidos; es fácil demostrar que la componente vertical de la fuerza de Coriolis en un flujo vertical está inundada por el equilibrio entre las dos grandes fuerzas que actúan verticalmente: presión y gravedad y, por lo tanto, es insignificante.

Figura\(\PageIndex{5}\): Un sistema de coordenadas útil en el plano tangente horizontal.

Figura\(\PageIndex{6}\): Resolviendo la aceleración de Coriolis en el plano tangente horizontal.

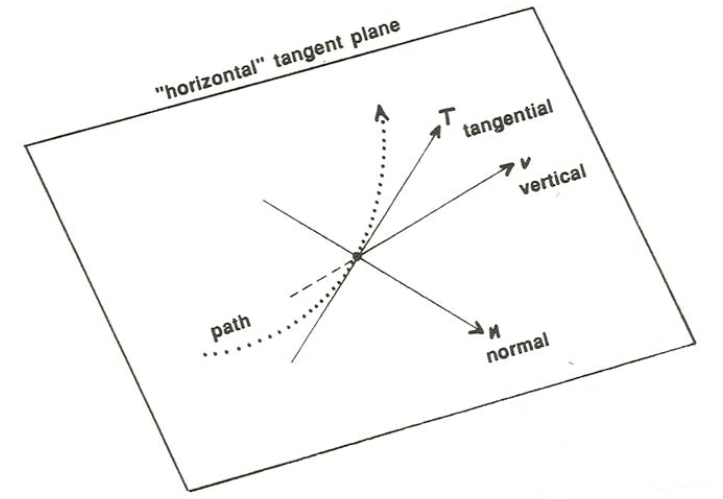
Ya has visto que el componente de la aceleración de Coriolis en la dirección del movimiento, el\(t\) eje en la Figura\(\PageIndex{6}\), es siempre cero. De lo que debemos preocuparnos es la magnitud de la componente horizontal de la aceleración de Coriolis en la dirección normal al movimiento horizontal, y cómo varía tanto con la latitud como con la dirección del movimiento dentro del plano horizontal. Voy a hacer esto de manera atajo mirando dos direcciones especiales, norte-sur y este-oeste.

Mire primero la orientación este-oeste. La aceleración de Coriolis se dirige normal a ambos \(v\)y \(\Omega\), que a un observador en el plano horizontal es un vector que se pega hacia el cielo hacia el sur y en un ángulo con la horizontal que es igual a\(90^{\circ}\) menos el ángulo de latitud\(\phi\). Por referencia a la Figura\(\PageIndex{7}\), si resuelve ese vector en el plano horizontal el componente tiene la magnitud 2\(v \omega \sin \phi\). Ahora mira la orientación norte-sur. Para un observador en el plano horizontal, el vector de aceleración de Coriolis es horizontal y apunta hacia el este para un movimiento hacia el norte y hacia el oeste para un movimiento hacia el sur. Por referencia a la Figura\(\PageIndex{8}\), la magnitud de la aceleración de Coriolis es nuevamente 2\(v \omega \sin \phi\). Si bien las matemáticas son mucho más intrincadas, resulta que la aceleración de Coriolis tiene esta misma magnitud, 2\(v \omega \sin \phi\), para cualquier dirección de movimiento en el plano horizontal.

Figura\(\PageIndex{7}\): Componente de la aceleración de Coriolis en la orientación este-oeste en el plano tangente horizontal.

Figura\(\PageIndex{8}\): Componente de la aceleración de Coriolis en la orientación norte-sur en el plano tangente horizontal.

Entonces, el resultado final de la aceleración de Coriolis para los movimientos horizontales en la superficie de la Tierra es esta:

1. Su magnitud es directamente proporcional a la velocidad del cuerpo,
2. Su componente horizontal siempre se dirige normal a la dirección de movimiento (a la derecha en el hemisferio norte pero a la izquierda en el hemisferio sur), y
3. Su magnitud es siempre 2\(v \omega \sin \phi\).

Por lo que el efecto Coriolis es mayor en los polos y cero en el Ecuador. (Funciona justo de la manera opuesta para el componente vertical de la aceleración de Coriolis —más grande en el Ecuador— pero, como dije antes, el componente vertical no es importante de todos modos). Lo que suele hacerse con esta expresión para la aceleración de Coriolis es extraer la\(v \omega \sin \phi\) parte 2 y llamarla el parámetro Coriolis, denotado por\(f\).

Por último, quiero asegurarme de que no confundas los efectos separados de la aceleración centrípeta y la aceleración de Coriolis, ambas que afectan el movimiento de los cuerpos en la superficie de la Tierra tal como lo ve un observador en la Tierra. La aceleración centrípeta afecta a todos los cuerpos dentro y sobre la Tierra, ya sean estacionarios o en movimiento. Para revelar su efecto, regrese a su plato giratorio y coloque una gran olla de agua poco profunda sobre él. Ya sabes lo que sucede cuando se gira la mesa: el agua se alza contra el lado exterior de la sartén, y la superficie del agua inclinada hacia adentro establece una componente horizontal de la fuerza de gravedad que contrarresta la fuerza centrífuga hacia afuera. Después de realizar el ajuste inicial en la pendiente de la superficie del agua, la fuerza centrífuga no tiene más efecto directo sobre el movimiento del agua en relación con un observador que monta sobre el plato giratorio. (Los lagos y océanos de la Tierra se ajustan de esta misma manera, al igual que la propia Tierra sólida. Es la razón por la que la Tierra es un esferoide oblato, con un diámetro ecuatorial mayor que el diámetro polo a polo, en lugar de una esfera). Debido a que la velocidad del agua relativa a los límites de la sartén es cero, no hay aceleración de Coriolis.

Ahora mueve la mano en el agua para producir una corriente suave en el interior del agua en la sartén. Por supuesto el patrón de flujo será modificado por fricción y eventualmente morirá, pero mientras el agua se mueve experimenta la aceleración de Coriolis, y la configuración de la corriente se ve más o menos fuertemente afectada, dependiendo de la velocidad del agua y la velocidad de rotación del plato giratorio. Son estos efectos en la atmósfera y los océanos los que vamos a investigar en el resto de este capítulo.