10.4: Carga de Cama

Estilos de movimiento de carga en cama a bajas intensidades de flujo

El transporte de las partículas superficiales en un lecho localmente plano produce una microtopografía distintiva, consistente en crestas y depresiones irregulares y discontinuas a pequeña escala orientadas aproximadamente paralelas al flujo. El espaciamiento de estas características sobre un lecho de arena es del orden de varios milímetros, y el relieve es muy pequeño, generalmente solo unos pocos diámetros de partícula. Este relieve lineado es un rasgo característico del transporte, para partículas que van desde tamaños de limo (Mantz, 1977) hasta al menos arena muy gruesa, y para condiciones hidráulicas que van desde justo por encima del umbral de movimiento de partículas hasta altas intensidades de flujo que producen condiciones de régimen superior, plano-lecho. Es la manifestación de las rayas de baja velocidad asociadas con el ciclo de ráfaga y barrido, descritas en el Capítulo 4.

No se precisan condiciones experimentales especiales para ver manifestaciones de esta microtopografía lineada. Aquí hay dos ejemplos cotidianos (bueno, casi). Es un día frío, gris, y la nieve acaba de comenzar a caer. Antes de que la superficie pavimentada de la carretera esté completamente blanqueada, se ven rayas blancas distintivas y cambiantes de nieve alineadas con el viento que sopla a través de la carretera. O estás parado en el fregadero de la cocina, lavando tubérculos frescos del jardín. La fracción fina del sedimento suelto se transporta en suspensión por el desagüe, para no volver a verse nunca más, pero la fracción más gruesa se forma inmediatamente en pequeñas rayas en la superficie del fregadero, debajo del agua que fluye rápidamente hacia el desagüe. Vuelva a la sección final del Capítulo 4, sobre estructuras coherentes en flujo turbulento, para conocer la dinámica detrás de estas rayas de carga de cama.

Las crestas y depresiones son producidas por la acción de pequeños pero fuertes remolinos turbulentos en el lecho. Exactamente cómo ocurre esto es cada vez más claro a medida que la estructura de turbulencia cerca del lecho se entiende mejor como resultado de numerosos estudios de laboratorio. La relevancia de estas observaciones para el movimiento de sedimentos ha sido discutida más a fondo por Grass (1971, 1974), Karcz (1973), Jackson (1976), Sumer y Oguz (1978), Bridge (1978), Sumer y Deigaard (1981) y Leeder (1983a).

La mayoría de las observaciones experimentales se han realizado en límites que son dinámicamente suaves o transitoriamente rugosos, es decir, en límites caracterizados por una subcapa viscosa que está al menos poco desarrollada. Pero las observaciones de límites dinámicamente ásperos (por ejemplo, por Grass, 1971) muestran que incluso para flujos sin una subcapa viscosa existe una región cercana al límite, que Grass llamó la “zona interna”, para\(y^{+} < 40\), caracterizada por rayas longitudinales distintivas de baja velocidad y una alternancia cuasicíclica de eventos que han llegado a ser conocidos como el ciclo de ráfaga y barrido (ver Capítulo 4). A medida que los fuertes vórtices con ejes transversales al flujo se acercan al límite, producen gradientes de presión que tienden a levantar las rayas y expulsarlas a la capa límite turbulenta. Este “estallido” de fluido de movimiento lento es capaz de transportar pequeñas partículas lejos del lecho a distancias unos centímetros por encima del lecho. Sumer y Oguz (1978) encontraron que las partículas cuya velocidad de sedimentación era del orden de\(0.5 u_{*}\) fueron transportadas “en un solo movimiento continuo” hasta elevaciones adimensionales\(y^{+}\) de\(100–200\). El fluido de movimiento lento en la ráfaga entonces se mezcla con, y es acelerado por, el fluido en la zona exterior, y algunos regresan al lecho como un vórtice de rápido movimiento o “barrido”, que a su vez crea una nueva explosión, y así sucesivamente. El proceso no es estrictamente periódico, aunque en promedio muestra un periodo y escala controlados principalmente por la velocidad y espesor de la capa límite turbulenta. Si el período de ráfagas es\(T\) y la velocidad lejos del lecho es\(U\), entonces\(U T / \delta=5\), dónde\(\delta\) está el grosor de la capa límite (en un flujo de canal abierto, la profundidad del flujo).

La existencia del ciclo explosión-barrido sugiere una explicación de los fenómenos de movimiento de partículas descritos anteriormente. Las ráfagas de movimiento de partículas a lo largo del lecho descritas por muchos trabajadores desde Vanoni (1964) probablemente corresponden a barridos de fluido en el ciclo de barrido de ráfagas, cuando los gradientes de velocidad cercanos al lecho, y por lo tanto las tensiones de cizallamiento, son localmente altos. Las partículas tienden a ser barridas hacia un lado u otro de rayas de fluido de movimiento rápido para reunirse bajo rayas de movimiento lento y producir la lineación de corriente característica observada en lechos planos.

Para arena más fina que aproximadamente\(0.6\)\(\mathrm{mm}\), el movimiento de partículas sobre un lecho plano eventualmente resulta en pequeñas acumulaciones de partículas que crecen para formar ondas (Capítulo 11). Luego, las ondas cambian el patrón de flujo en el lecho y, por lo tanto, también la interacción del flujo y las partículas de sedimento en movimiento. La separación del flujo tiene lugar en la cresta ondulada, y la capa límite se restablecerá aguas abajo de donde el flujo se vuelve a unir al lecho, en el lado stoss de la siguiente ondulación aguas abajo. Aunque la superficie del lecho es ahora mucho más irregular, la misma superficie lineada que se ve en un lecho plano generalmente se puede observar en los lados superiores de las ondas o formas de lecho más grandes, si el agua es clara y hay buena iluminación de ángulo bajo.

Quizás la forma menos difícil de observar cómo se mueven las partículas de carga de cama a medida que la intensidad del flujo aumenta más allá del umbral de movimiento es estudiar el movimiento de una sola partícula sobre un lecho compuesto por partículas similares que se mantienen en su lugar por un adhesivo. El único problema con tales experimentos, aunque no uno serio, es que no hay intercambio entre las partículas en movimiento y el lecho sedimentario: mientras no está en movimiento, la partícula de prueba siempre descansa alta, en una posición muy expuesta, y nunca puede moverse a una posición baja (a menudo llamada bolsillo) recientemente desocupado por otra partícula arrastrada. Tales experimentos han sido reportados por Meland y Norrman (1966), Francis (1973), Abbott y Francis (1977), y Nakagawa et al. (1980). Por valiosos que sean estos estudios de partículas únicas, sin embargo, no hay sustituto para observar el movimiento de las partículas de carga de lecho en lechos de sedimentos reales. Las dificultades observacionales son formidables: se necesita agua clara (sin carga suspendida para oscurecer la vista), una vista ampliada de cerca e, idealmente, filmación o grabación de video a alta velocidad, porque la rapidez con que cambia el estado de movimiento de las partículas hace que no sea muy productivo observar movimientos de partículas en tiempo real.

Meland y Norrman (1966) distinguieron tres etapas del movimiento de partículas:

1. En la etapa de movimiento “stop-and-go”, la partícula está atrapada durante una parte del tiempo entre otras partículas en el lecho. Esta etapa sigue al inicio del movimiento y es especialmente típica de partículas más pequeñas que el material del lecho promedio. En esta etapa un incremento muy pequeño\(u_{*}\) por encima del valor crítico produce un marcado incremento en la tasa promedio de movimiento de las partículas, que sin embargo está controlada principalmente por el lecho y el tamaño de partícula.
2. En la etapa de movimiento continuo en contacto con el lecho, la partícula rueda o roza sobre la superficie del lecho.
3. En la etapa más alta, las partículas comienzan a elevarse por encima del nivel del lecho o a realizar saltos largos. Los aumentos en la velocidad de las partículas son aproximadamente proporcionales a los aumentos en la velocidad de

Francis (1973) también distinguió tres modos de movimiento, aunque no se corresponden exactamente con las etapas descritas por Meland y Norrman:

1. laminación de partículas en contacto con el lecho (aproximadamente equivalente a las etapas 1 y 2 de Meland y Norrman);
2. salación, con partículas que se elevan hasta alturas de aproximadamente dos a cuatro diámetros de partícula por encima del lecho y luego retrocediendo a lo largo de trayectorias “balísticas”, como se ilustra en la Figura\(\PageIndex{1}\); y
3. suspensión, en la que al principio las partículas se mueven en “saltos” que se distinguen de la salación por su longitud y trayectorias sinuosas (Figura\(\PageIndex{1}\)), pero a medida que la suspensión se desarrolla mejor las partículas se elevan más por encima del lecho y regresan a él con menos frecuencia.

Figura\(\PageIndex{1}\): Croquis de trayectorias típicas de partículas observadas por Francis (1973). Arriba: trayectoria de saltación. Abajo: trayectoria de suspensión (línea ondulada, con trayectoria de saltación mostrada a la misma escala para comparación. (De Francis, 1973.)

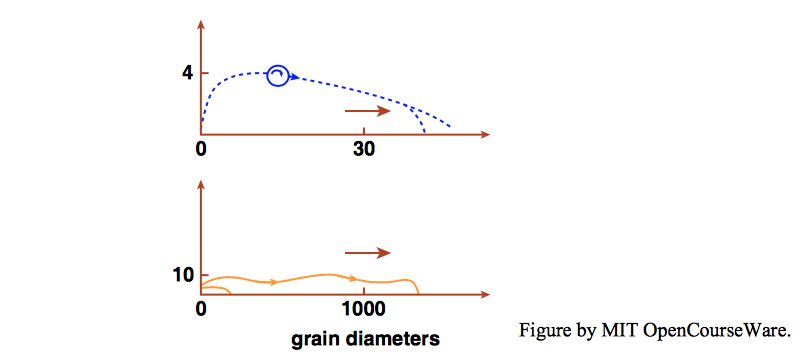
Francis (1973) distinguió la salación de la suspensión sobre la base de una evaluación cualitativa de la trayectoria de las partículas. Abbott y Francis (1977, p. 229) sugirieron una definición más rigurosa: una partícula está en saltación cuando “salta lejos del lecho y sigue una trayectoria tal que su aceleración vertical siempre se dirige hacia abajo entre los impulsos ascendentes sostenidos mientras está en contacto con el lecho”. Si en algún momento la aceleración vertical se dirige hacia arriba, entonces se considera que la partícula está en suspensión. Según esta definición, el hecho de que una partícula esté o no en suspensión no puede determinarse simplemente a partir de la observación cualitativa: se necesita un análisis detallado de la componente vertical de su aceleración, basado en la fotografía de alta velocidad de su trayectoria. La discusión adicional sobre la naturaleza de la salación (que está mejor desarrollada en el aire que en el agua) se aplazará hasta que hayamos examinado algunos de los resultados experimentales sobre la relación entre la intensidad del flujo y la velocidad de movimiento de los sedimentos. El modo de movimiento a velocidades de cizallamiento justo por encima del valor umbral\(u_{*c}\) predicho por el diagrama Shields fue investigado por Abbott y Francis (1977), con los resultados mostrados en la Figura\(\PageIndex{2}\).

Figura\(\PageIndex{2}\): Trayectorias de una esfera de vidrio saltante calculadas para el caso de arrastre solamente (esfera no giratoria) y arrastre más elevación (una esfera que gira 275 veces por segundo) en comparación con la trayectoria observada. Se puede observar que el hilado produjo un gran efecto tanto en la forma de la trayectoria como en la altura máxima de subida. (De White y Schultz, 1977.)

Los primeros movimientos\(u_{*}/u_{*c}\) de las partículas, aproximadamente\(1\) (correspondientes a\(u_{*}/w\) aproximadamente\(0.15\)), son por balanceo, pero a medida que aumenta la intensidad del flujo, la salación se convierte rápidamente en el modo dominante de movimiento de las partículas. Para el momento\(u_{*}/w\) ha alcanzado valores de solo aproximadamente\(0.3\), aproximadamente\(50\%\) de las trayectorias de las partículas se clasifican como estando en el modo de suspensión, utilizando la estricta definición de Abbott y Francis (1977), pero las partículas siguen caminos que aún están muy cerca del lecho, y la velocidad promedio de las partículas,\(U_{G}\), es aproximadamente proporcional a la velocidad de cizallamiento. (\(U_{G}/u_{*}\)está\(6\) a punto de\(8\), lo que indica que la velocidad de la partícula es casi igual a la del flujo cercano al lecho) A lo\(u_{*}/w = 0.5\) sumo las trayectorias serían clasificadas por Abbott y Francis (1977) como en el modo de suspensión, pero las partículas siguen moviéndose principalmente cerca de la cama en un modo que podría ser descrito subjetivamente por la mayoría de los observadores como más parecido a la saltación que a la suspensión verdadera.

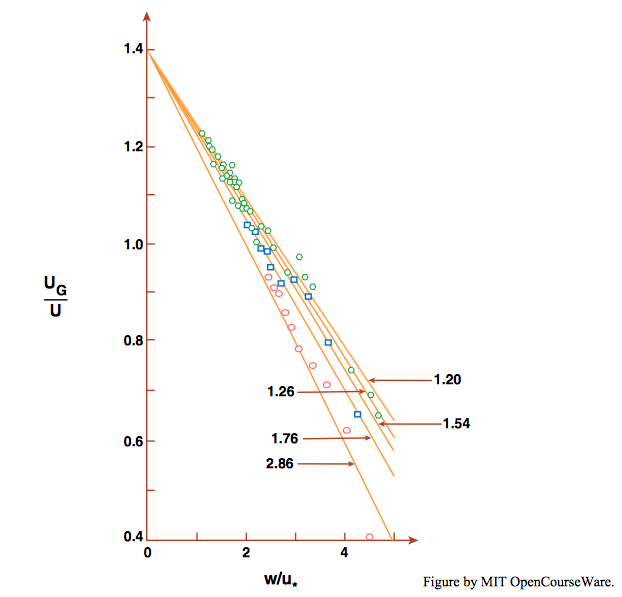
A medida que las intensidades de flujo se incrementan aún más, las trayectorias de las partículas se vuelven más largas e irregulares y las partículas son transportadas más altas al flujo A estas intensidades más altas parece más razonable normalizar la velocidad promedio del movimiento de las partículas dividiendo por la velocidad media del flujo\(U\) (una propiedad del flujo principal) que dividiendo por la velocidad de cizallamiento\(u_{*}\) (una propiedad del flujo justo por encima del lecho). Abbott y Francis (1977, y ver Francis, 1973) encontraron que para partículas de igual densidad\(U_{G}/U\) estaba directamente relacionado con\(w/u_{*}\), el recíproco de\(u_{*}/w\) (Figura\(\PageIndex{3}\)). A\(u_{*}/w\) mayor que\(0.5\) la velocidad promedio de las partículas fue en realidad mayor que la velocidad media del flujo, porque la mayoría de las trayectorias llevaron a las partículas hacia las partes más altas y, por lo tanto, que se mueven más rápidamente del flujo. (Experimentos anteriores reportados por Francis, 1973, sugieren que en la mayoría de los casos\(U_{G}/U\) no se\(u_{*}/w\) acerca\(1\) hasta enfoques\(1\).) Esto es congruente con el criterio de suspensión\(u_{*} > w\),, introducido en una fracción anterior.

Figura\(\PageIndex{3}\): Gráfica de velocidad de partícula adimensional\(U_{G}/U\) vs. la relación de velocidad de sedimentación de partículas a velocidad de cizallamiento,\(w/u_{*}\). Diferentes símbolos y líneas se refieren a partículas experimentales de diferentes gravedades específicas. (De Abbott y Francis, 1977.)

En su modelo estocástico pionero para el movimiento de partículas, Einstein (1950) postuló que la distancia promedio recorrida por una partícula que se mueve como carga de lecho no depende de la intensidad del flujo. Fernández Luque (1974; véase también Fernández Luque y van Beek, 1976), en observaciones de partículas que se mueven sobre un lecho plano suelto a tensiones de cizallamiento solo ligeramente mayores que las críticas, se encontró a partir de la observación directa que la longitud promedio de los “pasos” de partículas individuales (o saltos de saltación) era una constante igual a \(16\)veces el diámetro de partícula. Las partículas aceleraron ligeramente al inicio de cada salto y desaceleraron al regresar a la cama pero generalmente no llegaron a descansar. En promedio una partícula saltó alrededor de\(18\) veces, para una longitud de paso total de diámetros de\(288\) partícula, antes de llegar a descansar. La velocidad promedio durante el movimiento se redujo por colisiones con la superficie del lecho a aproximadamente\(85\%\) la velocidad máxima alcanzada en cada salto.

Se han realizado pocos estudios observacionales de los movimientos de partículas de carga de lecho en flujos sobre lechos de sedimentos sueltos en lugar de inmovilizados. Drake et al. (1988), en un estudio que muestra cuánta información sobre los movimientos de partículas se puede obtener mediante observación cuidadosamente ordenada, registraron los movimientos de partículas de carga de cama en el lecho de una corriente de agua clara mediante cinematografía de alta velocidad. El arroyo era\(6.45\)\(\mathrm{m}\) ancho y\(0.35\)\(\mathrm{m}\) profundo, y el lecho consistió en arena y grava moderadamente clasificadas con un tamaño mediano de\(4\)\(\mathrm{mm}\). Durante la filmación, el esfuerzo cortante del lecho era aproximadamente\(6\)\(\mathrm{Pa}\), que era aproximadamente el doble del umbral para el movimiento. Hubo movimiento activo de carga de cama, pero la concentración de carga del lecho no fue tan grande como para oscurecer los movimientos de las partículas. Las partículas se movieron principalmente por laminación, aunque las más finas se movieron por salación, y las partículas grandes y angulares se movieron por deslizamiento breve, empujando partículas más pequeñas fuera del camino. Los tiempos de desplazamiento de las partículas individuales, que duraron unas décimas de segundo, fueron mucho más cortos que los tiempos de reposo. La figura\(\PageIndex{4}\) muestra trayectorias representativas de cuatro partículas, de diversos tamaños, como se ve en vista lateral, tomadas de los marcos de imagen en movimiento.

Figura\(\PageIndex{4}\): Trayectorias típicas de carga de cama de cuatro partículas de diferentes tamaños, trazadas a partir de imágenes en movimiento de alta velocidad de vista lateral en una corriente con tamaño medio de material de lecho de 4 mm. La velocidad de filmación, en fotogramas por segundo, se da para cada trayectoria. (De Drake et al., 1988.)

Efecto de la Forma

El movimiento de las partículas sobre el lecho se ve fuertemente afectado por su forma. Las partículas tienden a orientarse sobre el lecho al pivotar alrededor de otras partículas o apoyarse contra ellas, y no necesariamente se orientan con su área de proyección máxima normal al flujo, como generalmente lo hacen durante la sedimentación. Ciertas formas, especialmente formas prolongadas (rodillos) pero también discos, ruedan más fácilmente que otras.

Un estudio experimental temprano del efecto de la forma fue realizado por Krumbein (1942) utilizando partículas elipsoidales artificiales, todas con el mismo diámetro nominal, en un canal con lecho liso. La profundidad se mantuvo constante a 0.3 m y la velocidad se varió cambiando la pendiente. Krumbein encontró que, para una velocidad de fluido dada, las esferas y los rodillos se movieron más rápido. Dentro de cualquier clase de forma (por ejemplo, rodillos), la velocidad de las partículas aumentó al aumentar la esfericidad; el efecto de forma fue mayor a bajas velocidades de fluido y velocidades de partículas, y fue menos importante ya que las partículas tendían a ser tomadas en suspensión.

Lane y Carlson (1954) encontraron que los guijarros que recubren los lechos de los canales de drenaje de Colorado estaban ordenados tanto por tamaño como por forma. En una muestra dada de guijarros de lecho, los guijarros en forma de disco tenían volúmenes sustancialmente más pequeños que los guijarros más esféricos, lo contrario de lo que sería el caso si los guijarros tuvieran la misma velocidad de sedimentación, lo que indica que los guijarros esféricos rodaban más fácilmente y se ponían en movimiento más fácilmente que en forma de disco guijarros, que tendían a asumir orientaciones más estables e imbricadas sobre la cama.

Bradley et al. (1972) estudiaron el efecto de la forma tanto en el campo (Knik River, Alaska) como en el laboratorio. Detectaron la clasificación de formas aguas abajo, siendo los guijarros laminados los más fáciles de transportar, luego los guijarros alargados (rodillos) y los guijarros más ecuantes siendo los menos fáciles de transportar. Reconocieron que las anomalías en los efectos de forma observados en diferentes investigaciones de campo y laboratorio probablemente son causadas por los diferentes efectos de clasificación de forma de partículas que se mueven por tracción y suspensión. El transporte más listo de los guijarros con hojas probablemente puede explicarse por su tipo de movimiento observado de “salación errática”, que tiende a elevar las partículas álabas hacia el flujo, de modo que a velocidades de fluido suficientemente altas su baja velocidad de sedimentación es más importante que su baja capacidad de enrollamiento.

Movimiento de carga de lecho a altas intensidades de flujo

A medida que aumenta la intensidad del flujo y la carga del lecho se vuelve más abundante, la capa de carga de lecho se vuelve más gruesa y la distancia de separación entre las partículas de carga de lecho se vuelve más pequeña Las dificultades de observar los detalles de los movimientos de las partículas en capas de carga de cama tan gruesas y de alta concentración se vuelven formidables, incluso se podría decir insuperables. Parece justo decir que la relación entre datos observacionales duros y deducción teórica es probablemente menor en esta área de transporte de sedimentos que en cualquier otra. La literatura está repleta de especulaciones sobre las fuerzas y movimientos involucrados.

Comenzamos con la obra clásica de Bagnold (1954, 1956), que ha jugado un papel tan importante en el pensamiento posterior. Bagnold realizó experimentos pioneros sobre fuerzas interpartículas en una mezcla fuertemente cizallada de agua y partículas sólidas. Los experimentos se realizaron en un pequeño aparato de sobremesa que constaba de dos cilindros concéntricos, con un delgado espacio anular entre ellos. El cilindro interior se mantuvo estacionario y se giró el cilindro exterior, dando un cizallamiento casi uniforme en el espacio anular, al igual que el hipotético experimento cocina-mesa descrito en el Capítulo 1. El espacio anular se llenó con agua que contenía una cierta concentración de partículas esféricas sólidas de flotación neutra. Para un rango de concentraciones de partículas y velocidades de rotación, Bagnold midió tanto el esfuerzo cortante como el esfuerzo normal en la pared del cilindro interno. Observó que tanto la tensión normal como la tensión cortante fueron superiores a las de concentración cero de partículas, y atribuyó estas tensiones, a las que llamó tensiones dispersivas, al efecto intuitivamente razonable de las fuerzas laterales engendradas por las interacciones de partículas en la mezcla cizallada. Tales interacciones podrían ser colisiones balísticas reales, aunque amortiguadas en mayor o menor grado por el fluido ambiental, o podrían implicar solo movimientos laterales de partículas causados por distorsiones del campo de flujo local por la presencia de partículas cercanas que se mueven a diferentes velocidades en el medio cizallado.

Es fácil desarrollar un marco adimensional en el que evaluar los resultados de los experimentos de Bagnold. Imagina que eres ingrávido, muy por encima de la Tierra en una estación espacial. Usted está equipado, de alguna manera, para hacer el experimento descrito en el Capítulo 1, cizallando un fluido entre placas paralelas, pero sin tener que preocuparse por fugas de fluido alrededor de los bordes. Estás en libertad de usar partículas de cualquier densidad, porque no tienes que preocuparte de que las partículas se asienten bajo su propio peso o sean centrifugadas en un dispositivo giratorio.

¿Qué variables regirían el esfuerzo dispersivo normal y el esfuerzo de cizallamiento dispersivo del tipo que Bagnold observó en sus experimentos (Figura 10-9)? El espaciamiento de las placas\(L\) y la velocidad relativa de la placa no\(V\) son importantes por sí mismos sino solo en combinación para dar la velocidad de cizallamiento\(V/L\); llamarlo\(R\). Los otros son directos: densidad y viscosidad del fluido, y densidad, tamaño y concentración de las partículas. Puede no dimensionalizar las tensiones de una manera similar a una partícula número de Reynolds:\((T / \rho)^{1 / 2} D / \mu\), y\((P / \rho)^{1 / 2} D / \mu\). Una variable adimensional independiente obvia es\(\rho_{s}/\rho\), la relación de densidad, y otra es la concentración\(C\) misma, si se toma como una concentración volumétrica. La tercera variable adimensional necesita involucrar la velocidad de cizallamiento; lo más natural es construir una variable en forma de un número de Reynolds,\(\rho R D^{2} / \mu\).

Los experimentos de Bagnold fueron más restringidos que su experimento de estación espacial, porque para evitar la centrifugación tuvo que usar partículas de flotación neutra. La implicación de ello es que los efectos dispersivos que encontró habrían sido aún mayores si\(\rho_{s}/ \rho\) hubieran sido mayores, como ocurre con el sedimento natural en el agua.

Las tensiones dispersivas observadas por Bagnold son ahora conocidas por ser importantes en una amplia gama de lo que se llama flujos de grano: flujos de partículas sólidas sueltas causadas por la fuerza directa de la gravedad, sin la necesaria implicación de un medio fluido. Los flujos de grano son importantes en ciertos ambientes naturales, como en avalanchas de nieve, ciertos tipos de deslizamientos de tierra y, en pequeñas escalas, la arena fluye por las caras de sotavento de las dunas de arena eólicas, y también en la tecnología.

Figura\(\PageIndex{5}\): El “caso de lecho de gravedad”: un flujo de cizallamiento turbulento en un campo de gravedad, transportando partículas de sedimento más densas que el medio fluido.

Bagnold (1956) dio el paso más allá de aplicar el concepto de tensiones dispersivas a lo que llamó el “caso de lecho de gravedad”: un flujo de fluido en un canal o conducto en un campo gravitacional, transportando partículas más densas cerca del lecho, como lo que llamaríamos, en el contexto de este capítulo, carga de lecho (Figura \(\PageIndex{5}\)). La idea es que si el flujo es lo suficientemente fuerte puede haber una capa más baja de sedimento transportado, con un espesor de muchos diámetros de partícula, en la que el cizallamiento es lo suficientemente fuerte como para que una tensión normal dispersiva haga su aparición y actúe para mantener la capa de carga de cama en un estado disperso. Bagnold teorizó que dentro de esta capa de carga de lecho esquilada y dispersa la turbulencia del fluido no es importante, en el sentido de que no es el agente principal el que mantiene las partículas en estado disperso. Estas ideas fueron elaboradas posteriormente por Dzulynski y Sanders (1962), quienes aplicaron el término alfombra de tracción (que es de uso común hasta nuestros días; ver, por ejemplo, Hiscott, 1994, 1995, y Sohn, 1995) al concepto, y por Moss (1972), quien introdujo el término capa reológica para esencialmente el mismo concepto. Una cita de Moss (1972, p. 162) captura bien la esencia del fenómeno:

A medida que el movimiento de carga de cama se vuelve más intenso en materiales del tamaño de arena, se alcanza una etapa en la que las colisiones entre partículas se vuelven inevitables y a partir de entonces la carga procede como una masa densa de partículas colisionantes, flotando por la presión dispersiva así generada... Esta masa móvil de partículas se comporta como un fluido viscoso, pero tiene un límite notablemente agudo con el flujo por encima y mantiene un espesor casi constante sobre áreas de lecho bastante grandes... (It) se llamará la “capa reológica”.

El problema es que aunque el concepto de capa de dispersión es consistente con la importancia bien establecida de las tensiones dispersivas en ciertos rangos de cizallamiento de mezclas de partículas y fluidos, nadie ha visto nunca dentro de una, debido a las obvias dificultades experimentales. (¡Un investigador, el escritor de estas notas! —una vez trató de superar las dificultades observacionales mediante la aparentemente ingeniosa técnica de utilizar la iluminación monocromática de partículas de sedimento transparentes que son transportadas en una capa concentrada de carga de lecho por un líquido transparente con exactamente el mismo índice de refracción que las partículas, en orden tener una visión clara y sin obstrucciones de algunas partículas opacas de líquido y sedimento marcadoras y registrar detalles de movimientos de partículas en el interior de la capa de carga de lecho utilizando cinematografía de alta velocidad. Sin embargo, nunca pudo lograr que funcionara lo suficientemente bien.) Hasta que la importancia del estrés dispersivo en las capas concentradas de carga de lecho se establezca por observación, en lugar de simplemente deducir, el concepto se considera mejor como hipotético y no como probado. Por supuesto, todavía pueden existir alfombras de tracción o capas reológicas; solo es cuestión de si las tensiones dispersivas u otros efectos como la turbulencia de fluidos a pequeña escala son el factor más importante en su dinámica.

Saltación en Agua

En el Capítulo 11 aprenderás que en el viento, la saltación es el modo principal, y muy característico, de movimiento de partículas. En la saltación, las partículas toman trayectorias largas, arqueadas por encima del lecho, poco influenciadas por la turbulencia en el flujo. Aquí abordamos la pregunta: ¿Cuál es la naturaleza y la importancia relativa de la saltación en el agua? La importancia de la saltación en el aire es clara, pero hay mucho menos acuerdo sobre su importancia en el agua. Las partículas saltantes se elevan mucho más por encima del lecho en el aire (comúnmente una fracción grande de un metro) que en el agua (solo unos pocos milímetros) debido al efecto mucho mayor del arrastre del fluido y al efecto reducido de la inercia de las partículas en el agua. Kalinske (1943) calculó que la altura a la que se elevarían las partículas saltantes, para un tamaño de partícula y una velocidad de cizallamiento dados, debería ser inversamente proporcional a la densidad del fluido, es decir, las partículas deberían elevarse\(800\) veces más en el aire que en el agua. También, el criterio de suspensión desarrollado en una sección anterior,\(u_{*} = w\), implica que las partículas deben ser llevadas relativamente fácilmente en suspensión en agua, debido a la velocidad de sedimentación mucho menor de las partículas en el agua que en el aire. Por lo tanto, la mayoría de los escritores de ingeniería (Einstein, 1950; Einstein y Chien, 1955; Ippen, 1971; Vanoni, 1975) han asumido que la suspensión por turbulencia es un mecanismo mucho más importante de transporte de sedimentos en los ríos que la saltación, incluso bastante cerca del lecho. En contraste con esta opinión, Bagnold (1956, 1973) ha argumentado que la verdadera saltación es independiente de la turbulencia, y que las altas concentraciones de partículas cercanas al lecho tienden a suprimir la turbulencia y hacen de la saltación (y colisiones de partículas) el mecanismo dominante de transporte de sedimentos.

Ciertas observaciones de Gordon et al. (1972), Fernández Luque (1974), Fernández Luque y van Beek (1976), y Abbott y Francis (1977) sugieren que el simple movimiento balístico de las partículas, y el movimiento por partículas que impactan en el fondo, pueden no ser tan importantes en el agua como algunos autores han sostenido. Gordon et al. (1972) estudiaron la salación de esferas de diámetro\(6.6\)\(\mathrm{mm}\) y gravedad específica\(1.3\) en un flujo de agua. El movimiento de las partículas se hizo esencialmente bidimensional al confinar el flujo dentro de un canal solo\(7.9\)\(\mathrm{mm}\) ancho. Las trayectorias observadas fueron típicas de la salación excepto que los ángulos de despegue fueron bastante bajos, generalmente en el rango de\(10^{\circ}\) a\(35^{\circ}\). Una razón del bajo ángulo de despegue fue que una partícula saltante no simplemente rebotaba en las partículas sueltas en el lecho; en cambio, la partícula en movimiento rodó alrededor de la partícula en el lecho antes de levantarse para hacer otro salto salatorio. Hubo una clara correlación entre la pérdida fraccional de energía cinética y el ángulo de incidencia en la colisión, pero las colisiones no fueron simples colisiones elásticas; parece claro que se involucró una combinación de inercia de partículas y fuerzas de arrastre de fluido. Tanto Fernández Luque (1974) como Abbott y Francis (1977), estudiando la saltación en agua, encontraron que muy pocas salaciones aparentes podían explicarse enteramente como simples trayectorias balísticas; algún otro tipo de fuerza de elevación estuvo involucrada en la mayoría de las trayectorias. Estos autores no investigaron los efectos de Magnus, pero parece probable (particularmente para los datos reportados por Francis) que el levantamiento principal fue proporcionado por turbulencias. Abbott y Francis (1977, p. 253) encontraron que “parece haber un rebote elástico efectivo entre el lecho y un grano móvil que incide sobre él”. Muy pocas salaciones observadas siguieron inmediatamente al retorno de una partícula al lecho; la mayoría fueron precedidas por algún balanceo. Además, no parecía haber diferencia en la velocidad de despegue entre las partículas que rebotan del lecho y las partículas que comienzan una salación desde reposo o rodando.

Murphy y Hooshiari (1982) estudiaron la salación de mármoles\(15.7\)\(\mathrm{mm}\) de diámetro sobre un lecho de mármoles similares pero fijos. La velocidad de sedimentación, aproximadamente\(0.8\)\(\mathrm{m/s}\), fue mucho mayor que las velocidades de cizallamiento necesarias para producir la salación continua (\(0.08–0.11\)\(\mathrm{m/s}\)), por lo que no hay duda de que la saltación más que la suspensión fue el modo dominante de movimiento. En este caso, las partículas parecían estar rebotando directamente del lecho, aunque el mecanismo exacto de elevación inicial desde el lecho no pudo ser estudiado por la técnica estroboscópica utilizada. El análisis de las trayectorias indicó que podrían ser contabilizadas satisfactoriamente por un modelo que tomara en cuenta la gravedad (y flotabilidad), los componentes horizontales y verticales del arrastre, y el efecto de masa adicionada que se produce al acelerar un sólido a través de un fluido (Hamilton y Courtney, 1977). Los efectos de Magnus no fueron significativos para partículas de este tamaño y forma en el agua. Las observaciones sugieren que las fuerzas de impacto del lecho son suficientes para producir la elevación ascendente, y que las fuerzas de elevación no son necesarias. Si esto es cierto (y no está probado, porque el lecho era rígido en el modelo, no suelto como lo sería en la naturaleza) entonces existe la posibilidad de que la salación de partículas más grandes (de tamaño de grava) en el agua pueda ser diferente a la de la arena en el agua. Puede ser que la salación de grava en agua se parezca más a la de la arena en el aire que a la de la arena en el agua.

Todas las observaciones descritas anteriormente se realizaron sobre flujos en los que muy pocas partículas estaban en salación. Posiblemente el arrastre fluido y la elevación juegan un papel muy reducido en el inicio y mantenimiento de la salación en una “alfombra de tracción”, pero las observaciones ciertamente sugieren severas limitaciones en una hipótesis de impacto simple para la salación a bajas concentraciones en el agua, e indican un papel muy significativo para la turbulencia en transporte de arena como carga de lecho.