14.3: Una mirada a algunos datos reales sobre tarifas de transporte fraccional, desde el canal y desde el campo

Ha habido una controversia de larga data sobre la realidad o importancia de la igualdad de movilidad desde que el concepto fue propuesto por primera vez por Parker et al. (1982b). Algunos conjuntos de mediciones, en canales y en arroyos, han mostrado un acercamiento cercano a la igualdad de movilidad, mientras que otros estudios han mostrado fuertes desviaciones de igual movilidad.

Primero observamos los resultados de los estudios de flujo más reveladores de las tasas de transporte fraccionario en sedimentos unimodales conformados hasta ahora. Wilcock y Southard (1989) realizaron un estudio de flume de las tasas de transporte fraccional en un canal de recirculación de sedimentos. El sedimento fue de tamaño mixto, con un tamaño medio\(1.83\)\(\mathrm{mm}\) y una distribución unimodal. En siete series con esfuerzo cortante creciente del lecho, las tasas de transporte fraccionarias de carga de cama de varias fracciones de tamaño, que variaban en tamaño de\(0.5\)\(\mathrm{mm}\) a\(6\)\(\mathrm{mm}\), se midieron mediante el uso de una trampa de ranura que se extendía a través del ancho del canal. Una vez pesadas, las muestras se devolvieron al sistema. El muestreo se realizó en dos momentos durante una ejecución: mientras que el lecho todavía estaba inicialmente plano, y en un momento posterior cuando el lecho y el flujo habían alcanzado el equilibrio. En las corridas con menor esfuerzo cortante del lecho, el lecho permaneció plano durante todo el recorrido, pero a mayores tensiones de cizallamiento del lecho, las dunas se desarrollaron en el lecho.

Figura\(\PageIndex{1}\): Velocidad de transporte fraccionario\( (p_{i}/f_{i})q_{b}\) vs. tamaño de partícula para siete ejecuciones con tensión de cizallamiento creciente del lecho. Cada curva representa un valor del esfuerzo cortante del lecho (no dado aquí). Estos datos se tomaron al final de cada serie, después de que el flujo y el lecho hubieran entrado en equilibrio con el flujo. (De Wilcock y Southard, 1988.)

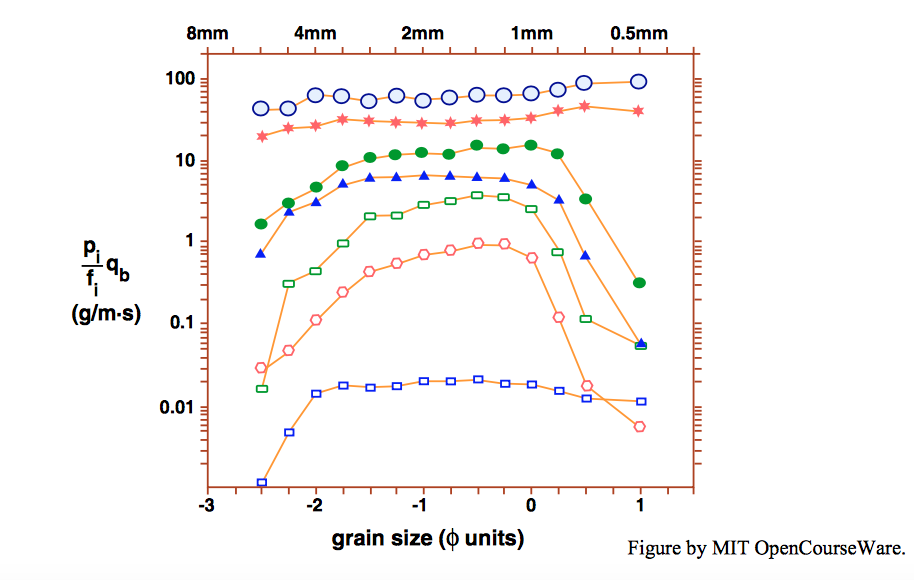
Se puede ver en la Figura\(\PageIndex{1}\) (compare esta figura con las Figuras 14.2.8 y 14.2.9) que para un amplio rango de fracciones de tamaño en la parte media de la distribución de tamaños las tarifas de transporte fraccional son casi las mismas: en otras palabras, hay un acercamiento cercano a la condición de movilidad igual para esas fracciones de tamaño. Sin embargo, salvo en los esfuerzos cortantes de lecho más altos, las curvas se apartan de las condiciones de movilidad igual: las tasas de transporte fraccionario tanto de las fracciones más finas como de las fracciones más gruesas son más difíciles de transportar. Podrías haber adivinado que las fracciones más gruesas serían más difíciles de transportar, pero es algo sorprendente que lo mismo sea cierto para las fracciones más finas.

Figura\(\PageIndex{2}\): Velocidad de transporte fraccionario\( (p_{i}/f_{i})q_{b}\) vs. tamaño de partícula para siete ejecuciones con tensión de cizallamiento creciente del lecho. Los símbolos sólidos son para las tasas de transporte fraccional inicial, y los círculos abiertos son para las tasas de transporte fraccional de equilibrio. (De Wilcock y Southard, 1988.)

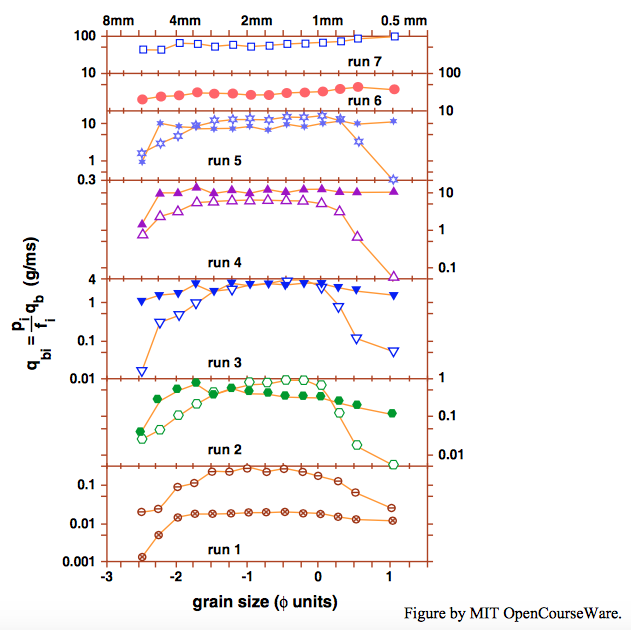
La figura\(\PageIndex{2}\), también de Wilcock y Southard (1988), repite los datos de la figura\(\PageIndex{1}\) pero también muestra los datos para las condiciones iniciales en las series (excepto para las dos a las mayores tensiones de cizallamiento del lecho). La principal diferencia en los datos entre las dos condiciones es que en la condición inicial las fracciones más finas se acercan más estrechamente a la condición de movilidad igual que en la condición de equilibrio. La explicación parece estar en una combinación de dos efectos:

1. A medida que pasa el tiempo, las partículas más finas encuentran su camino hacia abajo entre las partículas más gruesas hacia posiciones debajo de la capa superficial; y
2. A medida que se desarrollan pavimentos gruesos en la superficie del lecho, las partículas más finas se ocultan del flujo de manera más efectiva.

El conjunto de datos más citado sobre las tasas de transporte fraccionario en arroyos naturales es el de Milhous (1973) de Oak Creek, un arroyo de lecho de grava en Oregón. Los datos de Oak Creek fueron utilizados por Parker et al. (1982b) en su trabajo clásico sobre el concepto de igualdad de movilidad.

La figura\(\PageIndex{3}\), una gráfica de los datos de Oak Creek sobre la tasa de transporte fraccional muestra, como era de esperar, que las tasas de transporte fraccional son una función de la fuerza de flujo considerablemente creciente. La versión adimensional de la tasa de transporte fraccional, llamada parámetro de carga de cama adimensional\(W_{i}^{*}\), es igual a\(\gamma^{\prime}q_{bvi}/f_{i}u_{*}^{3}\). (Nota: la tasa de transporte fraccional, denotada aquí por\(q_{bvi}\), es por volumen de sedimento, no masa de sedimento.) El motivo de la separación de las curvas para las distintas fracciones de tamaño es que la variable adimensional en el eje horizontal,\ tau_ {i} ^ {*} (=\ tau_ {\ text {o}}/\ gamma^ {\ prime} D_i), contiene el tamaño\(D_{i}\) de partícula de la fracción dada.

Figura\(\PageIndex{3}\): Gráfica del parámetro de carga de cama adimensional\(W_{i}^{*}\) frente al esfuerzo cortante de lecho adimensional\(\tau_{i}^{*}\) para diez rangos de tamaño en los datos de Oak Creek. (De Parker et al., 1982b.)

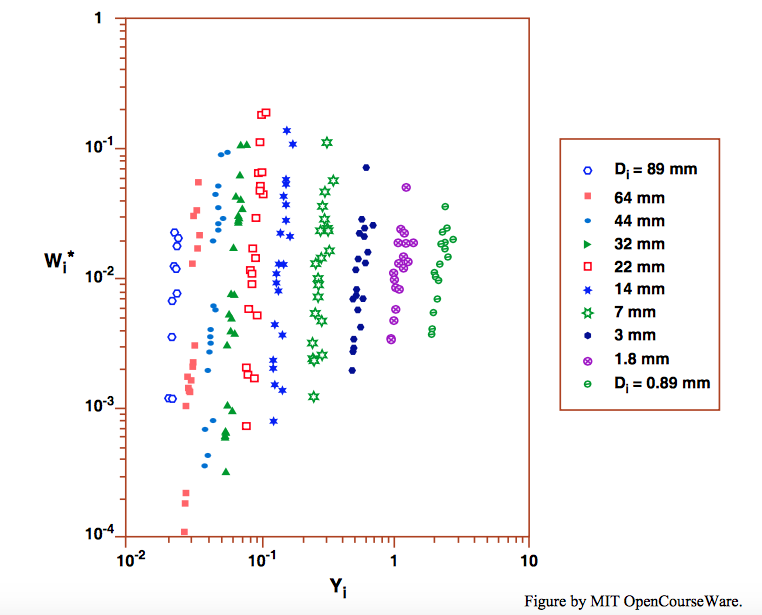
Cada curva en la Figura\(\PageIndex{3}\) se extrapoló hacia abajo para encontrar el esfuerzo cortante umbral, definido como el valor para el cual\(W_{i}^{*}\) se encontraba en un valor de referencia arbitrariamente elegido de\(0.002\) (elegido para ajustarse a lo que coincidiría con la condición comúnmente aceptada del umbral de movimiento; ver la discusión sobre el método de la tasa de referencia-transporte para definir el umbral de movimiento, en el Capítulo 9). Luego, en una gráfica de\(W_{i}^{*}\) versus\(\tau^{*}_{r}/\tau^{*}_{ri}\), que Parker et al. denotan por\(\phi_{i}\), todas las diez curvas para la tasa de transporte fraccional en la Figura\(\PageIndex{3}\) colapsan en una sola curva, no perfectamente, sino a una aproximación bastante buena (Figura\(\PageIndex{4}\)).

Figura\(\PageIndex{4}\): Cortesía de la Sociedad Americana de Ingenieros Civiles. Usado con permiso. A) Parcela de\(W_{i}^{*}\) vs. (\ tau^ {*} _ {r}/\ tau^ {*} _ _ {ri}\) para los datos de Oak Creek. B) La misma parcela, con rangos de tamaño dados. (De Parker et al., 1982b.)

(Aquí, la variable adimensional\(\phi_{i} = tau^{*}_{r}/\tau^{*}_{ri}\) puede necesitar atención cuidadosa por su parte: es el valor de referencia del esfuerzo cortante adimensional del lecho al que la tasa de transporte de carga total adimensional es igual a la tasa de transporte total de carga en cama de referencia, dividido por el valor de referencia del adimensional esfuerzo cortante de lecho de la fracción de tamaño\(i\) th a la que la velocidad de transporte adimensional de carga en cama de la fracción\(i\) ésima es igual a la tasa de transporte de carga de lecho de referencia de la fracción\(i\) th. (Esa larga frase requiere una lectura cuidadosa.) Básicamente, expresa la magnitud relativa del esfuerzo cortante del lecho adimensional en condición de umbral de referencia para el sedimento a granel, por un lado, y el esfuerzo cortante del lecho adimensional en la condición de referencia para la fracción\(i\) th, por otro lado.)

¿Cuál es entonces el significado de este “colapso” de las curvas individuales en una sola curva? Si vuelves a la sección sobre el experimento mental y miras la Figura 14.2.7, para la condición de perfecta movilidad igual, puedes ver que la Figura\(\PageIndex{4}\) es de la misma naturaleza, porque el efecto de tener el tamaño de partícula en el denominador de la tensión de cizallamiento del lecho adimensional es eludido tomando la relación de las dos tensiones de cizallamiento adimensionales del lecho. La conclusión a sacar es que también en el caso de este arroyo natural de lecho de grava se aborda la condición de igual movilidad, aunque no se cumple exactamente. Debemos concluir, entonces, que los efectos de ocultar-refugio y enrollabilidad se combinan, de alguna manera, para hacer que el transporte de las diversas fracciones de tamaño sea más casi igual, cuando se normaliza por las proporciones de las fracciones en la mezcla, aunque todavía hay una tendencia a que las fracciones más gruesas sean menores fácil de transportar.