8.6: Ejemplos de Derivaciones
- Page ID
- 103666
Ejemplo\(\PageIndex{1}\)
Dar una\(\Log{LK}\) derivación para el secuente\(A \land B \Sequent A\).
Comenzamos escribiendo la secuencia final deseada en la parte inferior de la derivación.
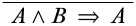
A continuación, necesitamos averiguar qué tipo de inferencia podría tener un secuente menor de esta forma. Esto podría ser una regla estructural, pero es una buena idea comenzar buscando una regla lógica. El único conectivo lógico que ocurre en el secuente inferior es\(\land\), entonces estamos buscando una\(\land\) regla, y como el\(\land\) símbolo aparece en el antecedente, estamos viendo la\(\LeftR{\land}\) regla.
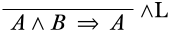
Hay dos opciones para lo que podría haber sido el secuente superior de la\(\LeftR{\land}\) inferencia: podríamos tener un secuente superior de\(A \Sequent A\), o de\(B \Sequent A\). Claramente,\(A \Sequent A\) es un secuente inicial (lo cual es algo bueno), mientras que no\(B \Sequent A\) es derivable en general. Rellenamos el secuente superior:
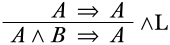
Ahora tenemos una correcta\(\Log{LK}\) -derivación del secuente\(A \land B \Sequent A\).
Ejemplo\(\PageIndex{2}\)
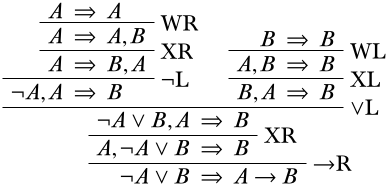
Dar una\(\Log{LK}\) derivación para el secuente\(\lnot A \lor B \Sequent A \lif B\).
Comience escribiendo la secuencia final deseada en la parte inferior de la derivación.
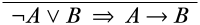
Para encontrar una regla lógica que nos pudiera dar esta secuencia final, observamos las conectivas lógicas en la secuencia final:\(\lnot\),\(\lor\), y\(\lif\). Solo nos importa en este momento\(\lor\) y\(\lif\) porque son operadores principales de oraciones en el final secuente, mientras que\(\lnot\) está dentro del alcance de otro conectivo, por lo que nos encargaremos de ello más adelante. Nuestras opciones de reglas lógicas para la inferencia final son, por tanto, la\(\LeftR{\lor}\) regla y la\(\RightR{\lif}\) regla. Podríamos escoger cualquiera de las reglas, en realidad, pero vamos a escoger la\(\RightR{\lif}\) regla (si por ninguna razón que no sea que nos permita poviar la división en dos ramas). De acuerdo con la forma de\(\RightR{\lif}\) inferencias que pueden producir el secuente inferior, esto debe verse así:
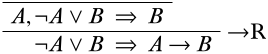
Si nos movemos\(\lnot A \lor B\) al exterior del antecedente, podemos aplicar la\(\LeftR{\lor}\) regla. Según el esquema, este debe dividirse en dos secuentes superiores de la siguiente manera:
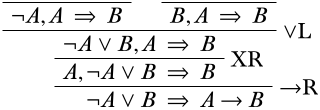
Recuerda que estamos tratando de abrirnos camino hasta las secuelas iniciales; ¡parece que estamos bastante cerca! La rama derecha es solo un debilitamiento y un intercambio de distancia de un secuente inicial y luego se hace:
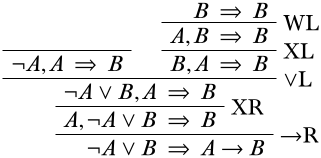
Ahora mirando a la rama izquierda, el único conectivo lógico en cualquier oración es el\(\lnot\) símbolo en las oraciones antecedentes, así que estamos viendo una instancia de la\(\LeftR{\lnot}\) regla.
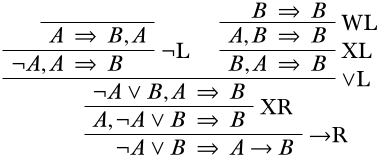
De manera similar a cómo rematamos la rama derecha, estamos a solo un debilitamiento y a un intercambio de rematar también a esta rama izquierda.
Ejemplo\(\PageIndex{3}\)
Dar una\(\Log{LK}\) -derivación de la secuencia\(\lnot A \lor \lnot B \Sequent \lnot (A \land B)\)
Usando las técnicas de arriba, comenzamos escribiendo el final final deseado en la parte inferior.
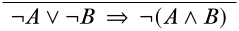
Las principales conexiones disponibles de oraciones en la secuencia final son el\(\lor\) símbolo y el\(\lnot\) símbolo. Funcionaría aplicar ya sea la regla\(\LeftR{\lor}\) o la\(\RightR{\lnot}\) regla aquí, pero comenzamos con la\(\RightR{\lnot}\) regla porque evita dividirse en dos ramas por un momento:
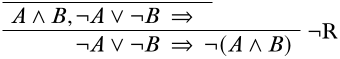
Ahora tenemos la opción de ver la regla\(\LeftR{\land}\) o la\(\LeftR{\lor}\) regla. Veamos qué pasa cuando aplicamos la\(\LeftR{\land}\) regla: tenemos la opción de comenzar ya sea con el secuente\(A, \lnot A \lor B \Sequent \quad\) o el secuente\(B, \lnot A \lor B \Sequent \quad\). Ya que la prueba es simétrica con respecto a\(A\) y\(B\), vamos con la primera:
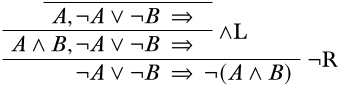
Continuando rellenando la derivación, vemos que nos encontramos con un problema:
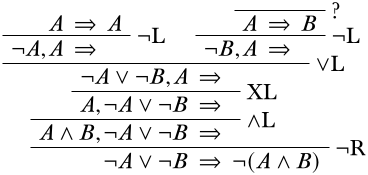
La parte superior de la rama derecha no se puede reducir más, y no se puede llevar a través de inferencias estructurales a un secuente inicial, por lo que este no es el camino correcto a seguir. Por lo que claramente, fue un error aplicar la\(\LeftR{\land}\) regla anterior. Volviendo a lo que teníamos antes y llevando a cabo la\(\LeftR{\lor}\) regla en su lugar, obtenemos
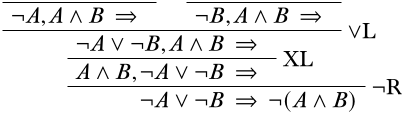
Completando cada sucursal como hemos hecho antes, obtenemos
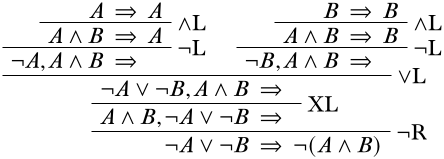
(Podríamos haber llevado a cabo las\(\land\) reglas inferiores a las\(\lnot\) reglas en estos pasos y aún así obtener una derivación correcta).
Ejemplo\(\PageIndex{4}\)
Hasta el momento no hemos utilizado la regla de contracción, pero a veces se requiere. Aquí hay un ejemplo donde eso sucede. Supongamos que queremos probar\(\quad \Sequent A \lor \lnot A\). Aplicar\(\RightR{\lor}\) al revés nos daría una de estas dos derivaciones:
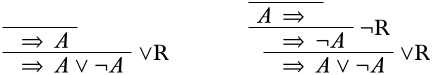
Ninguno de estos por supuesto termina en un secuente inicial. El truco es darnos cuenta de que la regla de contracción nos permite combinar dos copias de una oración en una, y cuando estamos buscando una prueba, es decir, yendo de abajo hacia arriba, podemos guardar una copia de\(A \lor \lnot A\) en la premisa, por ejemplo,
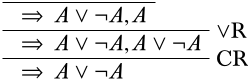
Ahora podemos aplicar\(\RightR{\lor}\) una segunda vez, y también obtener\(\lnot A\), lo que lleva a una derivación completa.

Problema\(\PageIndex{1}\)
Dar derivaciones de los siguientes secuentes:
-
\(\Sequent \lnot(A \lif B) \lif (A \land \lnot B)\)
-
\((A \land B) \lif C \Sequent (A \lif C) \lor (B \lif C)\)


