9.6: Derivaciones con cuantificadores
- Page ID
- 103617
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Ejemplo\(\PageIndex{1}\)
Al tratar con cuantificadores, tenemos que asegurarnos de no violar la condición de variable propia, y a veces esto nos obliga a jugar con el orden de llevar a cabo ciertas inferencias. En general, ayuda a tratar de cuidar primero las reglas sujetas a la condición de variable propia (serán más bajas en la prueba terminada).
Veamos cómo daríamos una derivación de la fórmula\(\lexists{x}{\lnot A(x)} \lif \lnot \lforall{x}{A(x)}\). Comenzando como de costumbre, escribimos

Empezamos por anotar lo que se necesitaría para justificar ese último paso usando la\(\Intro{\lif}\) regla.
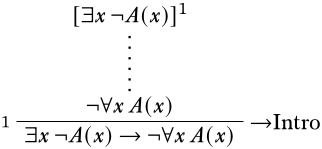
Dado que no hay una regla obvia a la que aplicar\(\lnot \lforall{x}{A(x)}\), procederemos configurando la derivación para que podamos usar la\(\Elim{\lexists{}{}}\) regla. Aquí debemos prestar atención a la condición de variable propia, y elegir una constante que no aparezca en\(\lexists{x}{A(x)}\) ni en ninguna suposición de la que dependa. (Sin embargo, dado que no aparecen símbolos constantes, cualquier elección funcionará bien).
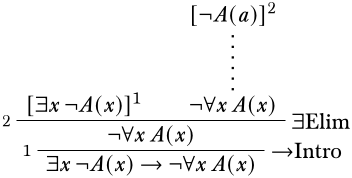
Para derivar\(\lnot \lforall{x}{A(x)}\), intentaremos usar la\(\Intro{\lnot}\) regla: esto requiere que derivemos una contradicción, posiblemente usando\(\lforall{x}{A(x)}\) como suposición adicional. Por supuesto, esta contradicción puede implicar el supuesto\(\lnot A(a)\) que se descargará por la\(\Intro{\lif}\) inferencia. Podemos configurarlo de la siguiente manera:
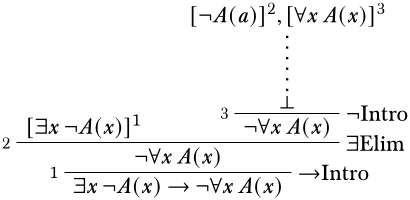
Parece que estamos cerca de conseguir una contradicción. La regla más fácil de aplicar es la\(\Elim{\lforall{}{}}\), que no tiene condiciones autovariables. Ya que podemos usar cualquier término que queramos reemplazar al universalmente cuantificado\(x\), tiene más sentido seguir usando para\(a\) que podamos llegar a una contradicción.
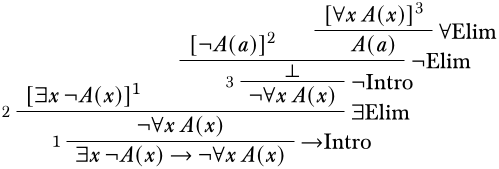
Es importante, especialmente cuando se trata de cuantificadores, verificar en este punto que no se ha violado la condición de variable propia. Dado que la única regla que aplicamos que está sujeta a la condición de variable\(\Elim{\exists}\) propia fue, y la variable\(a\) propia no ocurre en ningún supuesto de que dependa, esta es una derivación correcta.
Ejemplo\(\PageIndex{2}\)
A veces podemos derivar una fórmula de otras fórmulas. En estos casos, es posible que tengamos suposiciones no descargadas. Es importante hacer un seguimiento de nuestras suposiciones así como del objetivo final.
Veamos cómo daríamos una derivación de la fórmula\(\lexists{x}{C(x,b)}\) a partir de los supuestos\(\lexists{x}{(A(x) \land B(x))}\) y\(\lforall{x}{(B(x) \lif C(x,b))}\). Empezando como de costumbre, escribimos la conclusión en la parte inferior.
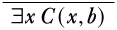
Tenemos dos premisas con las que trabajar. Para usar el primero, es decir, tratar de encontrar una derivación\(\lexists{x}{C(x, b)}\) de\(\lexists{x}{(A(x) \land B(x))}\) usaríamos la\(\Elim{\lexists{}{}}\) regla. Dado que tiene una condición de variable propia, aplicaremos esa regla primero. Obtenemos lo siguiente:
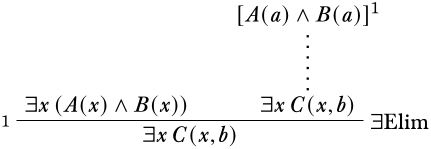
Los dos supuestos con los que estamos trabajando comparten\(B\). Puede ser útil en este punto aplicar\(\Elim{\land}\) para separar\(B(a)\).
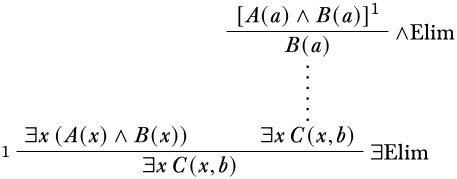
El segundo supuesto con el que tenemos que trabajar es\(\lforall{x}{(B(x) \lif C(x,b))}\). Como no hay condición de variable propia podemos instanciar\(x\) con el símbolo constante\(a\) usando\(\Elim{\lforall{}{}}\) para obtener\(B(a) \lif C(a, b)\). Ahora tenemos ambos\(B(a) \lif C(a,b)\) y\(B(a)\). Nuestro siguiente paso debería ser una aplicación sencilla de la\(\Elim{\lif}\) regla.

¡Estamos tan cerca! Una aplicación de\(\Intro{\lexists{}{}}\) y hemos alcanzado nuestro objetivo.
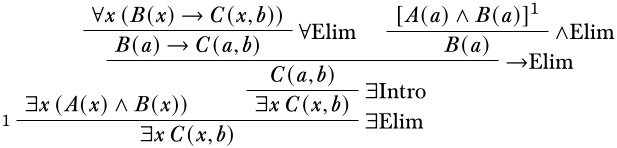
Dado que aseguramos en cada paso que no se violaron las condiciones de la variable propia, podemos estar seguros de que esta es una derivación correcta.
Ejemplo\(\PageIndex{3}\)
Dar una derivación de la fórmula\(\lnot\lforall{x}{A(x)}\) a partir de los supuestos\(\lforall{x}{A(x)} \lif \lexists{y}{B(y)}\) y\(\lnot\lexists{y}{B(y)}\). Comenzando como de costumbre, escribimos la fórmula objetivo en la parte inferior.
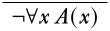
La última línea de la derivación es una negación, así que intentemos usar\(\Intro{\lnot}\). Esto requerirá que descubramos cómo derivar una contradicción.
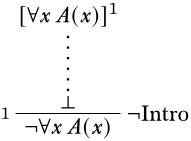
Hasta el momento tan bueno. Podemos usar\(\Elim{\lforall{}{}}\) pero no es obvio si eso nos ayudará a llegar a nuestro objetivo. En cambio, usemos una de nuestras suposiciones. \(\lforall{x}{A(x)} \lif \lexists{y}{B(y)}\)junto con nos\(\lforall{x}{A(x)}\) permitirá usar la\(\Elim{\lif}\) regla.
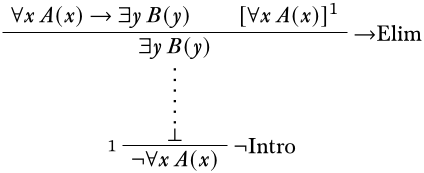
Ahora tenemos una suposición final con la que trabajar, y parece que esto nos ayudará a llegar a una contradicción mediante el uso\(\Elim{\lnot}\).
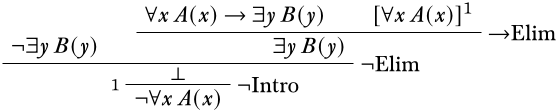
Problema\(\PageIndex{1}\)
Dar derivaciones de lo siguiente:
-
\(\lexists{y}{A(y)} \lif B\)de la suposición\(\lforall{x}{(A(x) \lif B)}\)
-
\(\lexists{x}{(A(x) \lif \lforall{y}{A(y)})}\)


