12.2: Representando Máquinas Turing
- Page ID
- 103687
Las máquinas de Turing se pueden representar visualmente mediante diagramas de estado. Los diagramas están compuestos por celdas de estado conectadas por flechas. Como era de esperar, cada celda de estado representa un estado de la máquina. Cada flecha representa una instrucción que se puede llevar a cabo desde ese estado, con los detalles de la instrucción escrita arriba o debajo de la flecha correspondiente. Considere la siguiente máquina, que tiene solo dos estados internos,\(q_0\) y\(q_1\), y una instrucción:
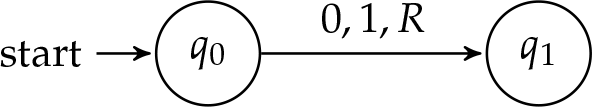
Recordemos que la máquina Turing tiene un cabezal de lectura/escritura y una cinta con la entrada escrita en ella. La instrucción se puede leer como si estuviera leyendo un estado\(\TMblank\) in\(q_0\), escriba a\(\TMstroke\), mueva a la derecha y pase al estado\(q_1\). Esto es equivalente a la función de transición\(\tuple{q_0, \TMblank}\) que mapea\(\tuple{q_1, \TMstroke, \TMright}\).
Ejemplo\(\PageIndex{1}\)
Incluso Máquina: La siguiente máquina de Turing se detiene si, y solo si, hay un número par de\(\TMstroke\)'s en la cinta (bajo el supuesto de que todo\(\TMstroke\) ha venido antes que el primero\(\TMblank\) en la cinta).
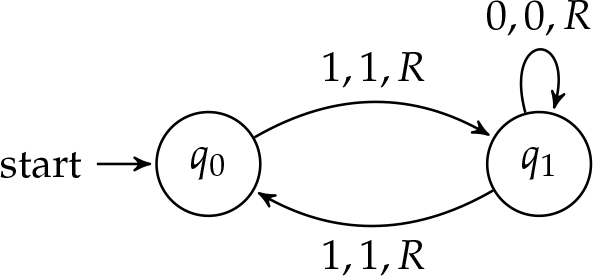
El diagrama de estados corresponde a la siguiente función de transición:
\[\begin{aligned} \delta(q_0, \TMstroke) & = \tuple{q_1, \TMstroke, \TMright},\\ \delta(q_1, \TMstroke) & = \tuple{q_0, \TMstroke, \TMright},\\ \delta(q_1, \TMblank) & = \tuple{q_1, \TMblank, \TMright}\end{aligned}\]
La máquina anterior se detiene solo cuando la entrada es un número par de golpes. De lo contrario, la máquina (teóricamente) continúa operando indefinidamente. Para cualquier máquina y entrada, es posible rastrear a través de las configuraciones de la máquina para determinar la salida. Daremos una definición formal de configuraciones más adelante. Por ahora, podemos pensar intuitivamente en las configuraciones como una serie de diagramas que muestran el estado de la máquina en cualquier momento durante la operación. Las configuraciones muestran el contenido de la cinta, el estado de la máquina y la ubicación del cabezal de lectura/escritura.
Rastreemos las configuraciones de la máquina par si se inicia con una entrada\(\TMstroke\) de cuatro. En este caso, esperamos que la máquina se detenga. Luego haremos funcionar la máquina en una entrada de\(\TMstroke\) tres's, donde la máquina funcionará para siempre.
La máquina arranca en estado\(q_0\), escaneando el más a la izquierda\(\TMstroke\). Podemos representar el estado inicial de la máquina de la siguiente manera:\[\TMendtape \TMstroke_0 \TMstroke \TMstroke \TMstroke \TMblank \ldots\nonumber\] La configuración anterior es sencilla. Como se puede ver, la máquina arranca en el estado uno, escaneando el más a la izquierda\(\TMstroke\). Esto está representado por un subíndice del nombre del estado en el primero\(\TMstroke\). La instrucción aplicable en este punto es\(\delta(q_0, \TMstroke) = \tuple{q_1, \TMstroke, \TMright}\), y así la máquina se mueve directamente sobre la cinta y cambia a estado\(q_1\). \[\TMendtape \TMstroke \TMstroke_1 \TMstroke \TMstroke \TMblank \ldots\nonumber\]Dado que la máquina está ahora en estado\(q_1\) escaneando a\(\TMstroke\), tenemos que “seguir” las instrucciones\(\delta(q_1, \TMstroke) = \tuple{q_0, \TMstroke, \TMright}\). Esto da como resultado la configuración\[\TMendtape \TMstroke \TMstroke \TMstroke_0 \TMstroke \TMblank \ldots\nonumber\] A medida que la máquina continúa, las reglas se aplican nuevamente en el mismo orden, dando como resultado las siguientes dos configuraciones:\[\TMendtape \TMstroke \TMstroke \TMstroke \TMstroke_1 \TMblank \ldots\nonumber\]\[\TMendtape \TMstroke \TMstroke \TMstroke \TMstroke \TMblank_0 \ldots\nonumber\] La máquina se encuentra ahora en estado\(q_0\) escaneando un \(\TMblank\). Con base en el diagrama de transición, podemos ver fácilmente que no hay instrucción a realizar, y así la máquina se ha detenido. Esto quiere decir que el insumo ha sido aceptado.
Supongamos que a continuación arrancamos la máquina con una entrada de\(\TMstroke\) tres's. las primeras configuraciones son similares, ya que se llevan a cabo las mismas instrucciones, con solo una pequeña diferencia de la entrada de cinta:\[\TMendtape \TMstroke_0 \TMstroke \TMstroke \TMblank \ldots\nonumber\]\[\TMendtape \TMstroke \TMstroke_1 \TMstroke \TMblank \ldots\nonumber\]\[\TMendtape \TMstroke \TMstroke \TMstroke_0 \TMblank \ldots\nonumber\]\[\TMendtape \TMstroke \TMstroke \TMstroke \TMblank_1 \ldots\nonumber\] La máquina ahora ha atravesado todos los\(\TMstroke\)'s, y está leyendo un estado\(\TMblank\) in\(q_1\). Como se muestra en el diagrama, hay una instrucción del formulario\(\delta(q_1, \TMblank) =\tuple{q_1, \TMblank, \TMright}\). Dado que la cinta se llena\(\TMblank\) indefinidamente a la derecha, la máquina continuará ejecutando esta instrucción para siempre, permaneciendo en estado\(q_1\) y avanzando cada vez más hacia la derecha. La máquina nunca se detendrá, y no acepta la entrada.
Es importante señalar que no todas las máquinas se detendrán. Si detener significa que la máquina se queda sin instrucciones para ejecutar, entonces podemos crear una máquina que nunca se detenga simplemente asegurando que hay una flecha saliente para cada símbolo en cada estado. La máquina uniforme se puede modificar para que funcione indefinidamente agregando una instrucción para escanear un\(\TMblank\) at\(q_0\).
Ejemplo\(\PageIndex{2}\)
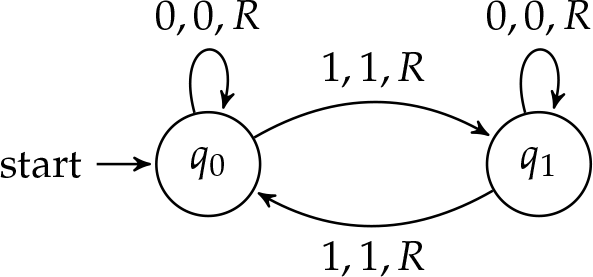
Las mesas de máquinas son otra forma de representar las máquinas Turing. Las mesas de máquinas tienen el alfabeto de cinta que se muestra en el\(x\) eje y el conjunto de estados de la máquina a través\(y\) del eje. Dentro de la tabla, en la intersección de cada estado y símbolo, se escribe el resto de la instrucción: el nuevo estado, el nuevo símbolo y la dirección del movimiento. Las mesas de máquina facilitan la determinación en qué estado y para qué símbolo, la máquina se detiene. Siempre que haya un hueco en la mesa es un punto posible para que la máquina se detenga. A diferencia de los diagramas de estado y conjuntos de instrucciones, donde los puntos en los que la máquina se detiene no siempre son obvios de inmediato, cualquier punto de detención se identifica rápidamente al encontrar los huecos en la mesa de la máquina.
Ejemplo\(\PageIndex{3}\)
La mesa de la máquina para la máquina uniforme es:
\ [\ begin {array} {|c|c|c|c|}
\ hline
&\ tmBlank &\ tmStroke &\ tMendTape\\ hline
q_0 & &\ tmTrans {\ tmStroke} {q_1} {\ tmDerecha} &
\ phantom {\ tmTrans {\ tmStroke} {q_1} {\ tmDerecha}}\\ hline
q_1 &\ TMTrans {\ tmBlank} {q_1} {\ tMright}
&\ tmTrans {\ tmStroke} {q_0} {\ tmDerecha} &
\ phantom {\ tmTrans {\ tmStroke} {q_1} {\ tmDerecha}}\\ hline
\ end {array}\ nonumber\]
Como podemos ver, la máquina se detiene al escanear un espacio en blanco en estado\(q_0\).
Hasta el momento sólo hemos considerado máquinas que leen y aceptan entrada. Sin embargo, las máquinas Turing tienen la capacidad tanto de leer como de escribir. Un ejemplo de tal máquina (aunque hay muchos, muchos ejemplos) es un doblador. Un doblador, cuando se inicia con un bloque de\(n\)\(\TMstroke\)'s en la cinta, emite un bloque de\(2n\)\(\TMstroke\)'s.
Antes de construir una máquina dobladora, es importante idear una estrategia para resolver el problema. Dado que la máquina (tal como la hemos formulado) no puede recordar cuántos\(\TMstroke\) ha leído, necesitamos encontrar una manera de hacer un seguimiento de todos los\(\TMstroke\)'s en la cinta. Una de esas formas es separar la salida de la entrada con un\(\TMblank\). Luego, la máquina puede borrar la primera\(\TMstroke\) de la entrada, atravesar el resto de la entrada, dejar una\(\TMblank\) y escribir dos\(\TMstroke\) nuevos.La máquina luego volverá y encontrará la segunda\(\TMstroke\) en la entrada, y también duplicará esa. Para cada uno\(\TMstroke\) de entrada, escribirá dos\(\TMstroke\) de salida. Al borrar la entrada a medida que va la máquina, podemos garantizar que no\(\TMstroke\) se pierda o se duplique dos veces. Cuando se borre toda la entrada, quedarán\(2n\)\(\TMstroke\)'s en la cinta. El diagrama de estados de la máquina Turing resultante se representa en la Figura\(\PageIndex{1}\).
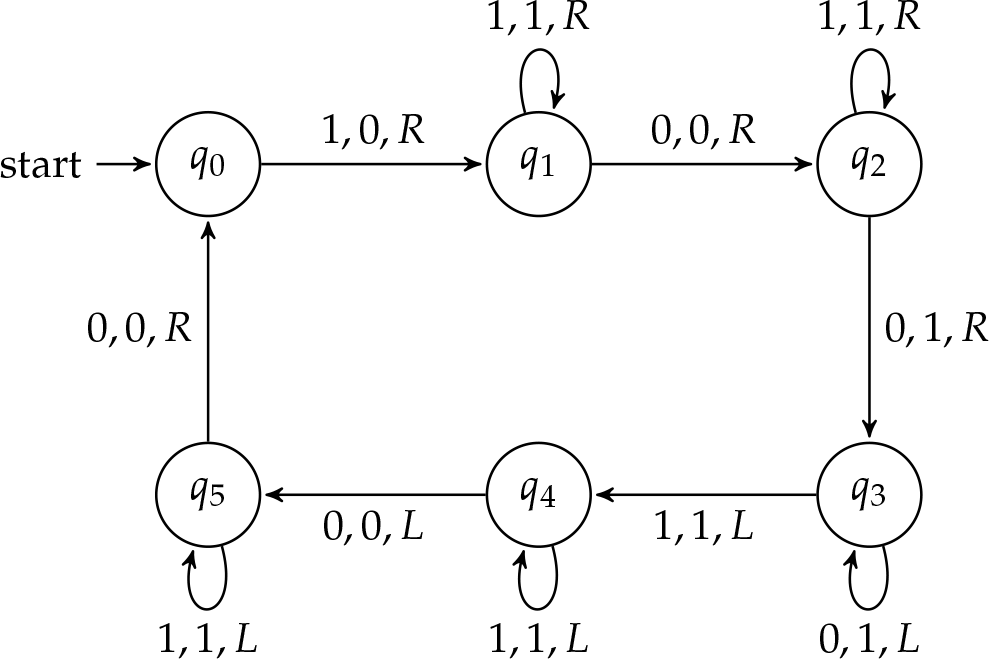
Problema\(\PageIndex{1}\)
Choose an arbitary input and trace through the configurations of the doubler machine in Example \(\PageIndex{4}\).
Problem \(\PageIndex{2}\)
The double machine in Example \(\PageIndex{4}\) writes its output to the right of the input. Come up with a new method for solving the doubler problem which generates its output immediately to the right of the end-of-tape marker. Build a machine that executes your method. Check that your machine works by tracing through the configurations.
Problem \(\PageIndex{3}\)
Design a Turing-machine with alphabet \(\{\TMendtape,\TMblank, A, B\}\) that accepts, i.e., halts on, any string of \(A\)’s and \(B\)’s where the number of \(A\)’s is the same as the number of \(B\)’s and all the \(A\)’s precede all the \(B\)’s, and rejects, i.e., does not halt on, any string where the number of \(A\)’s is not equal to the number of \(B\)’s or the \(A\)’s do not precede all the \(B\)’s. (E.g., the machine should accept \(AABB\), and \(AAABBB\), but reject both \(AAB\) and \(AABBAABB\).)
Problem \(\PageIndex{4}\)
Design a Turing-machine with alphabet \(\{\TMendtape,\TMblank, A, B\}\) that takes as input any string \(\alpha\) of \(A\)’s and \(B\)’s and duplicates them to produce an output of the form \(\alpha\alpha\). (E.g. input \(ABBA\) should result in output \(ABBAABBA\)).
Problem \(\PageIndex{5}\)
Alphabetical?: Design a Turing-machine with alphabet \(\{\TMendtape,\TMblank, A, B\}\) that when given as input a finite sequence of \(A\)’s and \(B\)’s checks to see if all the \(A\)’s appear to the left of all the \(B\)’s or not. The machine should leave the input string on the tape, and either halt if the string is “alphabetical”, or loop forever if the string is not.
Problem \(\PageIndex{6}\)
Alphabetizer: Design a Turing-machine with alphabet \(\{\TMendtape,\TMblank, A, B\}\) that takes as input a finite sequence of \(A\)’s and \(B\)’s rearranges them so that all the \(A\)’s are to the left of all the \(B\)’s. (e.g., the sequence \(BABAA\) should become the sequence \(AAABB\), and the sequence \(ABBABB\) should become the sequence \(AABBBB\)).


