3.4: Argumentos analógicos
- Page ID
- 101219
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Cuando golpee un cerillo producirá una llama. Es natural tomar el golpe del fósforo como la causa que produce el efecto de una llama. Pero, ¿y si la caja de cerilla está mojada? ¿O qué pasa si me encuentro en un vacío en el que no hay oxígeno (como en el espacio exterior)? Si alguna de esas cosas es el caso, entonces el golpe del partido no producirá una llama. Entonces no es simplemente el golpeo del partido lo que produce la llama, sino una combinación del golpe del partido junto con una serie de otras condiciones que deben estar en su lugar para que el golpeo del partido cree una llama. Cuál de esas condiciones llamamos la “causa” depende en parte del contexto. Supongamos que estoy en el espacio exterior golpeando un fósforo (supongamos que llevo un traje espacial que me abastece de oxígeno pero que estoy golpeando el fósforo en el espacio, donde no hay oxígeno). Lo golpeo continuamente pero no aparece ninguna llama (claro). Pero entonces alguien (también en traje espacial) saca una lata de oxígeno comprimido que rocían sobre el partido mientras yo lo golpeo. De repente se produce una llama. En este contexto, parece que es la fumigación de oxígeno lo que provoca la llama, no el golpeo del fósforo. Al igual que en el caso del golpe del partido, cualquier causa es más compleja que un simple evento que produce algún otro evento. Más bien, siempre hay múltiples condiciones que deben existir para que ocurra cualquier causa. Estas condiciones se denominan condiciones de fondo. Dicho esto, muchas veces damos por sentadas las condiciones de fondo en contextos normales y solo nos referimos a un evento en particular como la causa. Así, llamamos al golpeo del cerillo la causa de la llama. No pasamos a especificar todas las demás condiciones que conspiraron para crear la llama (como la presencia de oxígeno y la ausencia de agua). Pero esto es más por conveniencia que por corrección. Por casi cualquier causa, hay una serie de condiciones que deben estar en su lugar para que se produzca el efecto. Estas se denominan condiciones necesarias (recordar la discusión de condiciones necesarias y suficientes del capítulo 2, sección 2.7). Por ejemplo, una condición necesaria de la iluminación del fósforo es que haya oxígeno presente. Una condición necesaria para que un automóvil funcione es que haya gasolina en el tanque. Podemos utilizar las condiciones necesarias para diagnosticar lo que ha salido mal en casos de mal funcionamiento. Es decir, podemos considerar cada condición a su vez para determinar qué causó el mal funcionamiento. Por ejemplo, si el partido no se enciende, podemos verificar para ver si los partidos están mojados. Si encontramos que los fósforos están mojados entonces podemos explicar la falta de la llama diciendo algo así como, “dejar caer los fósforos en el agua provocó que los fósforos no se encendieran”. En contraste, una condición suficiente es aquella que si está presente siempre provocará el efecto. Por ejemplo, una persona que es alimentada a través de una astilladora operadora es suficiente para provocar la muerte de esa persona (como fue el destino del personaje de Steve Buscemi en la película Fargo). Debido a que el mundo natural funciona de acuerdo con las leyes naturales (como las leyes de la física), las causas pueden generalizarse. Por ejemplo, cualquier objeto cercano a la superficie de la tierra caerá hacia la tierra a 9.8 m/s2 a menos que lo impida alguna fuerza contraria (como la propulsión de un cohete). Esta generalización se aplica a manzanas, rocas, personas, astilladoras de madera y cualquier otro objeto. Tales generalizaciones causales son a menudo parte de las explicaciones. Por ejemplo, podemos explicar por qué el avión se estrelló contra el suelo citando la generalización causal de que todos los objetos no soportados caen al suelo y al señalar que el avión había perdido cualquier método de propulsión porque los motores habían muerto. Entonces invocamos la generalización causal al explicar por qué se estrelló el avión. Las generalizaciones causales tienen una forma particular:
Para cualquier x, si x tiene la (s) función (s) F, entonces x tiene la función G
Por ejemplo:
Para cualquier humano, si ese humano ha sido alimentado a través de una astilladora de madera operativa, entonces ese humano está muerto.
Para cualquier motor, si ese motor no tiene combustible, entonces ese motor no funcionará.
Para cualquier objeto cercano a la superficie de la tierra, si ese objeto no es soportado y no se ve obstaculizado por alguna fuerza contraria, entonces ese objeto caerá hacia la tierra a 9.8 m/s 2.
Poder determinar cuándo son verdaderas las generalizaciones causales es una parte importante de convertirse en un pensador crítico. Dado que tanto en contextos científicos como cotidianos nos apoyamos en generalizaciones causales para explicar y entender nuestro mundo, la capacidad de evaluar cuándo es verdadera una generalización causal es una habilidad importante. Por ejemplo, supongamos que estamos tratando de averiguar qué causa que nuestro perro, Charlie, tenga convulsiones. Para simplificar, supongamos que tenemos un conjunto de posibles candidatos para lo que causa sus convulsiones. Podría ser:
A) comer comida humana,
B) el champú que usamos para lavarlo,
C) su tratamiento de pulgas,
D) no comer a intervalos regulares,
o alguna combinación de estas cosas. Supongamos que llevamos un registro de cuándo ocurren estas cosas cada día y cuándo ocurren sus convulsiones (S). En la siguiente tabla, voy a representar la ausencia del rasgo por una negación. Entonces en la siguiente tabla, “~A” representa que Charlie no comió comida humana ese día; “~B” representa que ese día no se bañó y champú; “~S” representa que ese día no tuvo una convulsión. En contraste, “B” representa que sí tenía baño y champú, mientras que “C” representa que ese día le dieron un tratamiento contra pulgas. Así es como se ve el registro:
| Día 1 | ~A | B | C | D | S |
| Día 2 | A | ~B | C | D | ~S |
| Día 3 | A | B | ~C | D | ~S |
| Día 4 | A | B | C | ~D | S |
| Día 5 | A | B | ~C | D | ~S |
| Día 6 | A | ~B | C | D | ~S |
¿Cómo podemos usar esta información para determinar qué podría estar causando que Charlie tenga convulsiones? Lo primero que nos gustaría saber es qué característica está presente cada vez que tiene una convulsión. Esta sería una condición necesaria (pero no suficiente). Y eso nos puede decir algo importante sobre la causa. La prueba de condición necesaria dice que cualquier característica candidata (aquí A, B, C o D) que esté ausente cuando la entidad objetivo (S) está presente se elimina como una posible condición necesaria de S. 3 En la tabla anterior, A está ausente cuando S está presente, por lo que A no puede ser una condición necesaria (es decir, día 1). D también está ausente cuando S está presente (día 4) por lo que D tampoco puede ser una condición necesaria. En contraste, B nunca está ausente cuando S está presente, es decir, cada vez que S está presente, B también está presente. Eso significa que B es una condición necesaria, con base en los datos que hemos recopilado hasta el momento. Lo mismo se aplica a C ya que nunca está ausente cuando S está presente. Observe que hay momentos en los que tanto B como C están ausentes, pero en esos días la entidad objetivo (S) también está ausente, por lo que no importa.
Lo siguiente que nos gustaría saber es qué característica es tal que cada vez que está presente, Charlie tiene una convulsión. La prueba que es relevante para determinar esto se denomina prueba de condición suficiente. La prueba de condición suficiente dice que cualquier candidato que esté presente cuando la característica objetivo (S) está ausente se elimina como una posible condición suficiente de S. En la tabla anterior, podemos ver que ninguna característica candidata es una condición suficiente para causar las convulsiones ya que para cada candidato (A, B, C, D) hay un caso (es decir, día) donde está presente pero que no ocurrió ninguna incautación. Si bien ninguna característica es suficiente para provocar las convulsiones (de acuerdo con los datos que hemos recopilado hasta ahora), aún es posible que ciertas características sean suficientes conjuntamente. Dos características candidatas son suficientes conjuntamente para una característica objetivo si y solo si no hay ningún caso en el que ambos candidatos estén presentes y sin embargo el objetivo esté ausente. Aplicando esta prueba, podemos ver que B y C son suficientes conjuntamente para la entidad objetivo ya que cada vez que ambos están presentes, la entidad objetivo siempre está presente. Así, a partir de los datos que hemos recopilado hasta el momento, podemos decir que la causa probable de las convulsiones de Charlie es cuando ambos le damos un baño y luego seguimos ese baño con un tratamiento de pulgas. Cada vez que esas dos cosas ocurren, tiene una convulsión (condición suficiente); y cada vez que tiene una convulsión, esas dos cosas ocurren (condición necesaria). Así, los datos recabados hasta el momento apoyan el siguiente condicional causal:
Cada vez que a Charlie se le da un baño de champú y un tratamiento contra pulgas, tiene una convulsión.
Si bien en el caso anterior, las condiciones necesarias y suficientes eran las mismas, no tiene por qué ser siempre así. En ocasiones condiciones suficientes no son condiciones necesarias. Por ejemplo, ser alimentado a través de una astilladora de madera es una condición suficiente para la muerte, ¡pero desde luego no es necesario! (Mucha gente muere sin ser alimentada a través de una astilladora de madera, por lo que no puede ser una condición necesaria para morir). En todo caso, determinar las condiciones necesarias y suficientes es una parte clave para determinar una causa.
Al analizar los datos para encontrar una causa es importante que probemos rigurosamente a cada candidato. Aquí hay un ejemplo para ilustrar pruebas rigurosas. Supongamos que en todos los días recabamos datos sobre Charlie comió comida humana pero que en ninguno de los días se le dio un baño y champú, como indica la siguiente tabla.
| Día 1 | A | ~B | C | D | ~S |
| Día 2 | A | ~B | C | D | ~S |
| Día 3 | A | ~B | ~C | D | ~S |
| Día 4 | A | ~B | C | ~D | S |
| Día 5 | A | ~B | ~C | D | ~S |
| Día 6 | A | ~B | C | D | S |
Ante estos datos, A pasa trivialmente la prueba de condición necesaria ya que siempre está presente (así, nunca puede haber un caso en el que A esté ausente cuando S esté presente). Sin embargo, para probar rigurosamente A como condición necesaria, tenemos que buscar casos en los que A no esté presente y luego ver si nuestra condición objetivo S está presente. Hemos probado rigurosamente A como condición necesaria solo si hemos recopilado datos en los que A no estuvo presente. De lo contrario, no sabemos realmente si A es una condición necesaria. De igual manera, B pasa trivialmente la prueba de condición suficiente ya que nunca está presente (así, nunca puede haber un caso donde B esté presente pero S esté ausente). Sin embargo, para probar rigurosamente B como condición suficiente, tenemos que buscar casos en los que B esté presente y luego ver si nuestra condición objetivo S está ausente. Hemos probado rigurosamente B como condición suficiente solo si hemos recopilado datos en los que B está presente. De lo contrario, no sabemos realmente si B es una condición suficiente o no.
En pruebas rigurosas, estamos buscando activamente (o tratando de crear) situaciones en las que una característica candidata falle una de las pruebas. Es por ello que al probar rigurosamente a un candidato para la prueba de condición necesaria, debemos buscar casos en los que el candidato no esté presente, mientras que al probar rigurosamente a un candidato para la prueba de condición suficiente, debemos buscar casos en los que el candidato esté presente. En el ejemplo anterior, A no se prueba rigurosamente como condición necesaria y B no se prueba rigurosamente como condición suficiente. Si estamos interesados en encontrar una causa, siempre debemos probar rigurosamente a cada candidato. Esto significa que siempre debemos tener una mezcla de diferentes situaciones donde los candidatos y los objetivos a veces estén presentes y a veces ausentes.
Las pruebas de condiciones necesarias y suficientes se pueden aplicar cuando las características del entorno están completamente presentes o completamente ausentes. Sin embargo, en situaciones donde las características del entorno siempre están presentes en algún grado, estas pruebas no funcionarán (ya que nunca habrá casos en los que las características estén ausentes y por lo tanto no se puedan aplicar pruebas rigurosas). Por ejemplo, supongamos que estamos tratando de averiguar si el CO2 es una causa que contribuye a temperaturas globales más altas. En este caso, no podemos muy bien buscar casos en los que el CO2 esté presente pero no lo estén las altas temperaturas globales (prueba de condición suficiente), ya que el CO2 y las altas temperaturas siempre están presentes en algún grado. Tampoco podemos buscar casos en los que el CO2 esté ausente cuando se presentan altas temperaturas globales (prueba de condición necesaria), ya que, nuevamente, el CO2 y las altas temperaturas globales siempre están presentes en algún grado. Más bien, debemos usar un método diferente, el método que J.S. Mill llamó el método de variación concomitante. En la variación concomitante buscamos cómo varían las cosas entre sí. Por ejemplo, si vemos que a medida que aumentan los niveles de CO2, las temperaturas globales también suben, entonces esto es evidencia de que el CO2 y las temperaturas más altas se correlacionan positivamente. Cuando dos cosas se correlacionan positivamente, a medida que una aumenta, la otra también aumenta a una tasa similar (o a medida que una disminuye, la otra disminuye a una tasa similar). En contraste, cuando dos cosas se correlacionan negativamente, a medida que una aumenta, la otra disminuye a un ritmo similar (o viceversa). Por ejemplo, si a medida que un departamento de policía aumentara el número de policías en la calle, el número de delitos denunciados disminuye, entonces el número de policías en la calle y el número de delitos denunciados se correlacionarían negativamente. En cada uno de estos ejemplos, podemos pensar que podemos inferir directamente la causa a partir de la correlación: el aumento de los niveles de CO2 está provocando el aumento de las temperaturas globales y el creciente número de policías en la calle está haciendo que la tasa de criminalidad baje. Sin embargo, no podemos inferir directamente la causalidad a partir de la correlación. La correlación no es causalidad. Si A y B están correlacionados positivamente, entonces hay cuatro posibilidades distintas con respecto a cuál es la causa:
1. A es la causa de B
2. B es la causa de A
3. Alguna tercera cosa, C, es la causa de que tanto A como B aumenten
4. La correlación es accidental
Para inferir qué causa qué en una correlación, debemos confiar en nuestro conocimiento general (es decir, las cosas que sabemos que son ciertas sobre el mundo), nuestro conocimiento científico y posiblemente otras pruebas científicas. Por ejemplo, en el caso del calentamiento global, no existe una teoría científica que explique cómo el aumento de las temperaturas globales podría provocar el aumento de los niveles de CO2, pero existe una teoría científica que nos permita comprender cómo el aumento de los niveles de CO2 podría aumentar las temperaturas globales promedio. Este conocimiento hace plausible inferir que los crecientes niveles de CO2 están provocando el aumento de las temperaturas globales promedio. En el caso policía/crimen, a partir de nuestro conocimiento previo podemos llegar fácilmente a una inferencia sobre el mejor argumento explicativo de por qué una mayor presencia policial en las calles bajaría la tasa delictiva, cuanto más policías en la calle, más difícil es para los delincuentes salirse con la suya porque hay menos lugares donde esos delitos pudieran ocurrir sin que el delincuente fuera capturado. Dado que los delincuentes no quieren arriesgarse a que los atrapen cuando cometen un delito, ver más policías alrededor hará que sean menos propensos a cometer un delito. En contraste, no hay una buena explicación de por qué la disminución de la delincuencia provocaría que hubiera más policías en la calle. De hecho, parecería ser todo lo contrario: si la tasa delictiva es baja, la ciudad debería recortar, o al menos mantenerse estable, el número de policías y poner esos recursos en otro lugar. Esto hace plausible inferir que es el aumento de policías en la calle lo que está provocando la disminución de la delincuencia.
A veces se pueden correlacionar dos cosas sin que ninguna de las dos cause la otra. Más bien, alguna tercera cosa es causarles a ambos. Por ejemplo, supongamos que Bob descubre una correlación entre despertarse con toda la ropa puesta y despertarse con dolor de cabeza. Bob podría intentar inferir que dormir con toda la ropa puesta causa dolores de cabeza, pero probablemente haya una mejor explicación que esa. Es más probable que Bob esté bebiendo demasiado la noche anterior le hizo desmayarse en su cama con toda la ropa puesta, así como su dolor de cabeza. En este escenario, la ebriedad de Bob es la causa común de que tanto su dolor de cabeza como su ropa esté puesta en la cama.
A veces las correlaciones son meramente accidentales, lo que significa que no hay ninguna relación causal entre ellas en absoluto. Por ejemplo, Tyler Vigen 4 reporta que el consumo per cápita de queso en Estados Unidos se correlaciona con el número de personas que mueren al enredarse en sus sábanas:
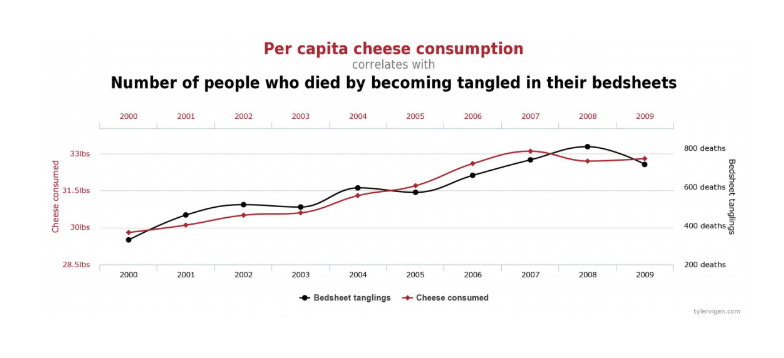
Y el número de limones mexicanos importados a Estados Unidos se correlaciona con el número de muertes por tránsito 5:
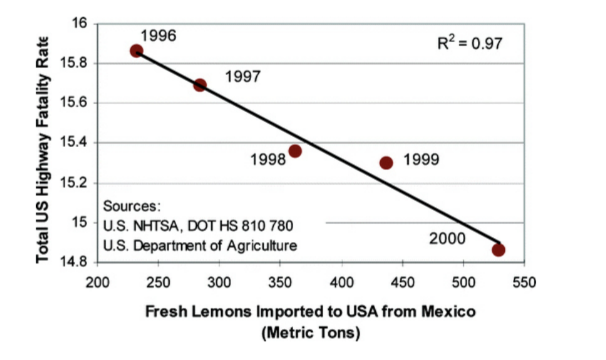
Claramente, ninguna de estas correlaciones está causalmente relacionada en absoluto, son correlaciones accidentales. Lo que los hace accidentales es que no tenemos ninguna teoría que tenga sentido de cómo podrían estar relacionados causalmente. Esto solo demuestra que no es simplemente la correlación lo que nos permite inferir una causa, sino, más bien, alguna teoría de fondo adicional, teoría científica, u otra evidencia que establece una cosa como causante de otra. Podemos explicar la relación entre correlación y causalidad utilizando los conceptos de condiciones necesarias y suficientes (introducidos por primera vez en el capítulo 2): la correlación es una condición necesaria para la causalidad, pero no es una condición suficiente para la causalidad.
Nuestra discusión de causas ha demostrado que no podemos decir que solo porque A precede a B o esté correlacionado con B, que A causó B. Atender que como A precede o correlaciona con B, A debe ser por lo tanto la causa de B es cometer lo que se llama la falacia de la causa falsa. A la falacia de causa falsa se le llama a veces la falacia “post hoc”. “Post hoc” es la abreviatura de la frase latina, “post hoc ergo propter hoc”, que significa “antes de esto por lo tanto por esto”. Como hemos visto, las falacias de causa falsa ocurren cada vez que alguien asume que dos eventos que se correlacionan deben estar en una relación causal, o que como un evento precede a otro, debe causar al otro. Para evitar la falacia de causa falsa, se debe examinar más cuidadosamente la relación entre A y B para determinar si existe una causa verdadera o solo una causa común o correlación accidental. Las causas comunes y las correlaciones accidentales son más comunes de lo que uno podría pensar.
Ejercicio
Determinar cuál de los candidatos (A, B, C, D) en los siguientes ejemplos pasa la prueba de condición necesaria o la prueba de condición suficiente en relación con el objetivo (G). Además, anote si hay candidatos que no sean rigurosamente probados como condiciones necesarias o suficientes.
1.
| Caso 1 | A | B | ~C | D | ~G |
| Caso 2 | ~A | B | C | D | G |
| Caso 3 | A | ~B | C | D | G |
2.
| Caso 1 | A | B | C | D | G |
| Caso 2 | ~A | B | ~C | D | ~G |
| Caso 3 | A | ~B | C | ~D | G |
3.
| Caso 1 | A | B | C | D | G |
| Caso 2 | ~A | B | C | D | G |
| Caso 3 | A | ~B | C | D | G |
4.
| Caso 1 | A | B | C | D | ~G |
| Caso 2 | ~A | B | C | D | G |
| Caso 3 | A | ~B | C | ~G | ~G |
5.
| Caso 1 | A | B | C | D | ~G |
| Caso 2 | ~A | B | C | D | G |
| Caso 3 | A | ~B | C | ~D | ~G |
6.
| Caso 1 | A | B | ~C | D | ~G |
| Caso 2 | ~A | B | C | D | ~G |
| Caso 3 | A | ~B | ~C | ~D | G |
7.
| Caso 1 | A | B | ~C | D | G |
| Caso 2 | ~A | ~B | C | D | ~G |
| Caso 3 | A | ~B | C | ~D | ~G |
8.
| Caso 1 | A | B | ~C | D | ~G |
| Caso 2 | ~A | ~B | ~C | D | ~G |
| Caso 3 | A | ~B | ~C | ~D | ~G |
9.
| Caso 1 | A | B | ~C | D | G |
| Caso 2 | ~A | ~B | C | D | G |
| Caso 3 | A | ~B | ~C | D | ~G |
10.
| Caso 1 | ~A | B | ~C | D | ~G |
| Caso 2 | ~A | B | C | D | G |
| Caso 3 | ~A | ~B | ~C | D | G |
Para cada una de las siguientes correlaciones, utilice sus conocimientos previos para determinar si A causa B, B causa A, una causa común C es la causa tanto de A como B, o las correlaciones son accidentales.
1. Existe una correlación positiva entre el gasto estadounidense en ciencia, espacio y tecnología (A) y los suicidios por ahorcamiento, estrangulación y asfixia (B).
2. Existe una correlación positiva entre el peso de nuestro perro Charlie (A) y la cantidad de tiempo que pasamos fuera de casa (B). Es decir, cuanto más tiempo pasamos fuera de casa, más pesado se vuelve Charlie (y cuanto más estamos en casa, más ligero es Charlie.
3. La altura del árbol en nuestro patio delantero (A) se correlaciona positivamente con la altura del arbusto en nuestro patio trasero (B).
4. Existe una correlación negativa entre el número de atentados suicidas con bombas en Estados Unidos (A) y el número de pelos en la cabeza de un presidente estadounidense en particular (B).
5. Existe una alta correlación positiva entre el número de camiones de bomberos en un determinado municipio de Nueva York Cite (A) y el número de incendios que allí ocurren (B).
6. En un momento de la historia, hubo una correlación negativa entre el número de mulas en el estado (A) y los salarios pagados a los profesores de la universidad estatal (B). Es decir, cuanto más mulas, menores serán los salarios de los profesores.
7. Existe una fuerte correlación positiva entre el número de accidentes de tránsito en una carretera particular (A) y el número de vallas publicitarias con modelos escasamente revestidos (B).
8. La circunferencia de la cintura de un adulto (A) se correlaciona negativamente con la altura de su salto vertical (B).
9. Los tiempos del maratón olímpico (A) se correlacionan positivamente con la temperatura durante el maratón (B). Es decir, cuanto más tiempo tarda un maratonista olímpico en completar la carrera, mayor es la temperatura.
10.El número de canas en la cabeza de un individuo (A) se correlaciona positivamente con el número de hijos o nietos que tiene (B).
3 Esta discusión se basa en gran medida en el capítulo 10, pp. 220-224 de Sinnott-Armstrong y
Understanding Argumentos de Fogelin, 9ª edición (Cengage Learning).
4 http://tylervigen.com/spurious-correlations
5 Stephen R. Johnson, El problema con QSAR (o Cómo aprendí a dejar de preocuparme y abrazar
la falacia). J. Chem. Inf. Modelo., 2008, 48 (1), pp. 25—26.


