11.3.4: La lógica de Si-Entonces
- Page ID
- 101943
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)En esta sección exploramos la lógica de los condicionales. Algunos patrones de argumento que involucran condicionales son tan comunes que se les ha dado nombres. El más común de todos es modus ponens:

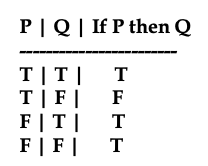
La validez de esta forma se puede verificar utilizando la tabla de verdad para su implicación (es decir, la condicional) y notando que no hay posibilidad de un contraejemplo, es decir, una situación en la que todas las premisas son verdaderas y la conclusión es falsa.
El lógico griego Chrysippus descubrió la forma modus ponens en el año 200 a.C.E. He aquí un ejemplo de un argumento cuya forma lógica sentencial es modus ponen s:
Si compraron tanto stock de aluminio justo antes de que Chile tuviera su huelga general, entonces serán aniquilados.
Sí compraron esa cantidad de acciones de aluminio justo antes de que Chile tuviera su huelga general.
Serán aniquilados.
Para demostrar que este argumento sí tiene la forma lógica modus ponens, podríamos usar este diccionario de abreviaturas:
P = Compraron tanto stock de aluminio justo antes de que Chile tuviera su huelga general.
Q = Serán aniquilados.
Si simbolizamos el argumento, entonces obtenemos esta forma lógica:

Elegir las letras P y Q fue arbitrario. Podríamos haber usado A y B. La siguiente forma también se llama modus ponens:
Si A entonces B
A
Entonces, B
Además del modus ponens, existen otras formas de razonamiento deductivamente válido en la lógica sentencial. El modus tollens es otro común, y tiene esta forma:

Ejemplos de esta forma de razonamiento válido se examinaron en capítulos anteriores sin mencionar el término latino para ello. Aquí hay un ejemplo:
Si es abogado, entonces sabe lo que significa la palabra agravio. Sorprendentemente, no sabe lo que significa la palabra. Entonces, no es abogado.
En este ejemplo de modus tollens, las letras A y B representan lo siguiente:
A = Es abogado.
B = Sabe lo que significa la palabra agravio.
En la vida cotidiana, no sería apto para detectar la forma modus tollens con tanta claridad porque el argumento anterior podría estar incrustado en un pasaje como este:
Si realmente fuera abogado como afirma, conocería la palabra agravio. Entonces, es una especie de impostor.
Este pasaje contiene el mismo argumento de modus tollens que estaba en el pasaje anterior. Sin embargo, la premisa no-B es ahora implícita. La conclusión del modus tollens también es implícita. Además, se ha llegado a una segunda conclusión, a saber, que es un impostor. Se necesita mucho más trabajo de detective lógico para descubrir el argumento del modus tollens.
Aunque la forma modus tollens es una forma válida —es decir, cualquier argumento con esa forma es un argumento válido—, aparentemente hay argumentos similares que son inválidos pero que a menudo se confunden con válidos. Aquí hay un ejemplo de uno común:
Si es brasileña, entonces habla portugués. Ella no es brasileña, así que no habla el idioma.
El razonamiento es deductivamente inválido. Para fines de lógica simbólica, trataremos a “Ella no es brasileña” como la misma frase que “Ella no es brasileña”. En forma estándar, el argumento se puede escribir de esta manera:
Si es brasileña, entonces habla portugués.
Ella no es brasileña.
—
Ella no habla portugués.
La conclusión no sigue con certeza. Supongamos que sí es cometer la falacia de negar el antecedente. La falacia también ocurre de manera más transparente en este argumento: “Si eres nazi, entonces respiras aire, pero obviamente no eres nazi, entonces no respiras aire”. Este argumento inválido es lógicamente análogo al de hablar portugués.
En la lógica sentencial, la forma lógica de la falacia es

La forma es lo que define la falacia. La parte if de un condicional, la P, se llama su antecedente. Entonces entonces parte se llama el consecuente. La segunda premisa, “no-P”, niega (niega) el antecedente. El arguer afirma lo condicional, niega el antecedente y hace una inferencia inválida. Por eso la falacia tiene el nombre que tiene.
Ejercicio\(\PageIndex{1}\)
¿Es válido el siguiente argumento?
Digamos que AI+ es inteligencia artificial que es algo mayor que el nivel humano. Es decir, AI+ es un poco más inteligente que el humano más inteligente. Habrá AI+. A lo mejor en una década o dos. Digamos que AI++ (o súper inteligencia) es IA de nivel mucho mayor que el humano (digamos, al menos tanto más allá del humano más inteligente como el humano más inteligente está más allá de un ratón). Es inevitable si se produce AI+.
- Contestar
-
Sí, es válido. Aquí está el argumento en forma estándar:
1. Habrá AI+.
2. Si hay AI+, habrá AI++.
─────────────────────────
3. Habrá AI++”.
Aquí hay un argumento inválido que a menudo se confunde con un argumento de modus ponens.
Si es brasileña, entonces habla portugués. Ella sí habla portugués. Entonces ella es brasileña.
Las premisas de este argumento sí dan una razón débil para creer que la mujer es brasileña. No obstante, si la arguer cree que las premisas establecen con certeza que ella es brasileña, entonces la arguer está cometiendo la falacia de afirmar lo consecuente. Reescribir el argumento en forma estándar rinde
Si es brasileña, entonces habla portugués.
Ella sí habla portugués.
—
Ella es brasileña.
La forma lógica, en la lógica sentencial, de la falacia es

La falacia de afirmar lo consecuente tiene su nombre porque la entonces parte de cualquier condicional se llama su consecuente y porque afirmar la segunda premisa Q afirma la consecuente del condicional.
Ejercicio\(\PageIndex{1}\)
¿Cuál pasaje comete la falacia de negar el antecedente?
a. Si los precios de la carne de cerdo continuaran bajando en Japón de 1789 a 1889, entonces el ciudadano promedio de Tokio habría comido el cerdo regularmente en 1890. Los precios de la carne de cerdo continuaron bajando en Japón durante ese tiempo. En consecuencia, el ciudadano promedio de Tokio en 1890 sí comió carne de cerdo regularmente.
b. Si los precios de la carne de cerdo continuaran bajando en Japón de 1789 a 1889, entonces el ciudadano promedio de Tokio habría comido la carne de cerdo regularmente en 1890. El ciudadano promedio de Tokio en 1890 no comía carne de cerdo regularmente. Entonces, los precios de la carne de cerdo no continuaron bajando en Japón de 1789 a 1889.
c. Si los precios de la carne de cerdo continuaran bajando en Japón de 1789 a 1889, entonces la carne de cerdo habría sido comida regularmente por el ciudadano promedio de Tokio en 1890. Por lo que el ciudadano promedio de Tokio en 1890 no comía carne de cerdo regularmente, porque los precios del cerdo no continuaron bajando en Japón de 1789 a 1889.
d. Si los precios de la carne de cerdo continuaran bajando en Japón de 1789 a 1889, entonces el ciudadano promedio de Tokio habría comido la carne de cerdo regularmente en 1890. El ciudadano promedio de Tokio en 1890 no comía carne de cerdo regularmente. Entonces, los precios de la carne de cerdo sí siguieron bajando en Japón de 1789 a 1889.
e. Si los precios de la carne de cerdo continuaran bajando en Japón de 1789 a 1889, entonces el ciudadano promedio de Tokio habría comido la carne de cerdo regularmente en 1890. El ciudadano promedio de Tokio en 1890 comía carne de cerdo regularmente. Entonces, los precios de la carne de cerdo sí siguieron bajando en Japón de 1789 a 1889.
- Contestar
-
Respuesta (c).

Ejercicio\(\PageIndex{1}\)
En el anterior Concept Check, ¿qué pasaje comete la falacia de afirmar lo consecuente?
- Contestar
-
Respuesta (e).

Ejercicio\(\PageIndex{1}\)
En el anterior Concept Check, ¿qué pasaje es un ejemplo de modus ponens?
- Contestar
-
Respuesta (a).
Los logísticos que trabajan en la lógica sentencial han descubierto muchas otras formas de argumento deductivamente válidas e inválidas. Por ejemplo:

Es decir, la siguiente forma argumental es deductivamente válida:

Si alguien te dice: “Si hoy nieva, deberías buscar refugio en la cabaña de David”, ¿la persona está insinuando que hoy está nevando? No, y el punto detrás de por qué la persona no es es captado por el siguiente formulario de argumento inválido:

La siguiente inferencia también es deductivamente inválida:

Te sorprendería cuánta gente comete esos dos errores.
Las técnicas de la lógica sentencial a menudo pueden ser útiles para analizar la argumentación deductiva, pero hay muchos argumentos deductivos para los que no se aplican los métodos sentenciales. El reconocimiento de este hecho ha llevado a los logísticos a crear nuevas y más poderosas lógicas para manejar estos otros argumentos. Estas lógicas se estudian en cursos universitarios llamados “lógica simbólica” y “lógica deductiva” y “lógica formal”.
Detectar la forma lógica de una oración es una habilidad sutil; no puedes hacerlo automáticamente. Si no tienes cuidado, entonces pensarás erróneamente que estas dos frases si-entonces son equivalentes, pero no lo son:
Si Oswald no le disparó al presidente Kennedy, entonces alguien más lo hizo.
Si Oswald no hubiera disparado al presidente Kennedy, entonces alguien más lo habría hecho.
La sutil diferencia en estas dos frases es que nuestro conocimiento previo nos dice, quizás implícitamente, evaluar la primera oración desde la perspectiva de nuestro presente, pero evaluar la segunda desde justo antes de que le dispararan al Presidente.
A veces los logísticos necesitamos prestar atención al estado de ánimo subjuntivo, y a veces no necesitamos hacerlo. Por ejemplo, las dos frases siguientes son equivalentes y pueden traducirse en lógica simbólica con el mismo símbolo, aunque la segunda esté en el estado de ánimo subjuntivo y la primera esté en el estado de ánimo indicativo:
Si te disparo, entonces morirás.
Si te disparara, entonces morirías.
Ejercicio\(\PageIndex{1}\)
Identificar la forma lógica del siguiente razonamiento sobre los condicionales, e indicar si es o no un razonamiento válido:
John: ¿Estás seguro?
Winona: Si no lo estuviera, no estaría aquí.
- Contestar
-
Este es un razonamiento válido. Que P sea la suposición implícita de que estoy aquí. Que Q sea el reclamo que estoy seguro. Entonces el razonamiento tiene esta forma lógica válida:
P
Si no Q,
entonces no P
—
Q


