14.1: Correlaciones
- Page ID
- 102121
Una correlación es una conexión o asociación entre dos tipos de cosas. Por ejemplo, a los científicos les interesan no sólo las estadísticas sobre quién tiene cáncer de pulmón, sino también en cómo se relaciona el tabaquismo con el cáncer de pulmón. Esta relación es de aparente conexión, y se describe matemáticamente diciendo que los valores de la variable “número de fumadores en un grupo” y la variable “número de casos de cáncer de pulmón en ese grupo” están correlacionados. La palabra correlacionada es un término técnico. Encontrar una correlación en tus datos entre dos variables A y B es una pista de que puede haber alguna historia causal para que descubras, como que A está causando B, o viceversa.

Supongamos que un artículo científico reporta que fumar se correlaciona positivamente con el cáncer de pulmón. Lo que esto significa o implica es que grupos de personas con un alto porcentaje de fumadores suelen tener también un alto porcentaje de casos de cáncer de pulmón, y los grupos con un bajo porcentaje de fumadores suelen tener también un bajo porcentaje de casos de cáncer de pulmón.
Aquí hay otra manera de hacer el mismo punto. Los dos porcentajes tienden a subir y caer juntos en muchos grupos. Si A = porcentaje de fumadores en cualquier grupo y B = porcentaje de casos de cáncer de pulmón en el mismo grupo, entonces el artículo científico informa que los valores de la variable A tienden a subir y bajar ya que los valores de la variable B también suben y bajan.
Definición
Si los valores de la variable A tienden a aumentar y disminuir en sincronía (paralela) con los valores de la variable B, entonces hay una correlación positiva entre los valores de A y los valores de B.
Cuando los valores de A y los valores de B están correlacionados positivamente, también decimos que las propias variables están correlacionadas positivamente.
La presión y el volumen de un gas contenido están correlacionados negativamente. Cuando aumentas la presión, usualmente notas una disminución en el volumen, y viceversa.
Definición
Si A tiende a aumentar cuando B disminuye y viceversa, entonces hay correlación negativa entre A y B.
Definición
Si A cambia al azar a medida que B cambia, entonces no hay correlación entre A y B.
Estar correlacionado es cuestión de grado. También estar correlacionado negativa o positivamente implica que las dos variables no son independientes entre sí. Si tuviéramos que borrar la frase tiende a partir de las dos primeras definiciones, tendríamos correlaciones perfectas. Cuando A siempre aumenta con aumentos en B, y siempre disminuye con disminuciones en B, entonces A y B están perfectamente correlacionados positivamente. Cuando los científicos dicen que dos variables son directamente proporcionales, significan que existe una perfecta correlación positiva de línea recta entre ellas. Una correlación negativa perfecta entre dos variables, como la presión y el volumen de un gas ideal, a menudo se expresa diciendo que son inversamente proporcionales. Las gráficas adjuntas muestran algunas de estas posibles relaciones entre dos variables A y B.


En las dos gráficas superiores, rectas, tenemos evidencia de que A es directamente proporcional a B. En la segunda, tenemos evidencia de que A es inversamente proporcional a B. Cuando A se correlaciona con B, se deduce con certeza que B se correlacionará con A, y viceversa. En otras palabras, la correlación es una relación simétrica. 1
Hemos introducido correlaciones hablando de variables, pero también pueden ocurrir correlaciones entre características. Por ejemplo, existe una correlación entre la característica de ser canadiense y la característica de poseer un abrigo cálido con capucha. La característica “ser canadiense” puede pensarse como una variable con dos valores “característica está presente” y “característica está ausente”. Es decir, la característica C puede pensarse como una variable con los posibles valores de “presente” y “ausente” o los valores C y Not-C. Con este tipo de variables, no tiene sentido hablar de sus valores “cambiando en sincronía”. Aquí hay algunas nuevas definiciones de correlación que se aplican a este tipo de características:
Definición
A se correlaciona positivamente con B en una población dada siempre que el porcentaje de A entre B sea mayor que el porcentaje de A entre los no B
Definición
A se correlaciona negativamente con B en una población dada siempre que el porcentaje de A entre los B sea menor que el porcentaje de A entre los no B.
Definición
A y B no están correlacionados si los porcentajes de A entre los B son los mismos que entre los no B.
Por ejemplo, ser alto se correlaciona positivamente con ser un jugador de basquetbol profesional porque encontrarás un mayor porcentaje de personas altas entre los jugadores que entre los no jugadores. Al aplicar la definición anterior de correlación positiva, dejaríamos
A = gente alta
B = jugadores de basquetbol profesionales
Non-B = personas que no son jugadores profesionales de basquetbol
¿Existe alguna correlación entre ser canadiense y tener un plátano en el patio trasero? Sí, definitivamente. Examinar aleatoriamente grupos de personas. Cuanto mayor sea el porcentaje de canadienses, menos personas en el grupo que tendrán un banano en su patio trasero. Hay una correlación negativa.
Ejercicio\(\PageIndex{1}\)
Dado nuestro conocimiento común sobre las carreras de caballos y los jinetes que montan los caballos, ¿existe alguna correlación entre el peso corporal de una persona y su ser un jockey profesional?
a. Sí, están correlacionados positivamente.
b. Sí, están correlacionados negativamente.
c. No, no están correlacionados.
- Contestar
-
Respuesta b). En un grupo de jinetes, se esperaría que el peso promedio fuera menor que el peso promedio de la mayoría de las personas en la sociedad
La correlación es cuestión de grado. Algunas correlaciones son fuertes; algunas son débiles. Si el porcentaje de personas con cáncer de pulmón fuera solo ligeramente superior entre los fumadores que entre los no fumadores, la correlación entre el cáncer de pulmón y el tabaquismo sería débil. En realidad, sin embargo, el porcentaje de personas con cáncer de pulmón es veinte veces mayor entre los fumadores que entre los no fumadores, por lo que la correlación es muy fuerte.
Definición
La fuerza de la correlación entre las características A y B es proporcional a la diferencia entre el porcentaje de B que son A y el porcentaje de No-B que son A. 2
Ejercicio\(\PageIndex{2}\)
¿Los impuestos estadounidenses sobre la renta están correlacionados con los ingresos brutos de los ciudadanos ¿Positiva o negativamente? ¿Fuerte o débilmente? ¿Perfectamente?
- Contestar
-
Los impuestos estadounidenses sobre la renta están correlacionados positivamente con los ingresos brutos de los ciudadanos. La correlación no es perfecta, pero es bastante fuerte. La correlación es débil en los tramos de ingresos más altos, donde esas personas tienden a pagar proporcionalmente un porcentaje bastante pequeño de sus ingresos en impuestos gracias a los refugios fiscales.
Algunas personas encuentran correlaciones donde otras no. Aquí hay una disputa que ocurrió hace muchos años. El cabildero de los Pescadores Asociados del Río Colorado afirmó que existe una correlación entre el número de lubinas rayadas en el río Colorado y la cantidad de agua sacada del río por el Estado de Nevada. Un desarrollador de viviendas en Las Vegas dijo que no ve correlación. ¿Quién es correcto? Bueno, veamos los datos. El cabildero y la vivienda desarrollada no están en desacuerdo sobre los datos brutos. Aquí hay algunas tablas de estos datos del siglo anterior:


¿Cómo puedes mirar estos dos conjuntos de datos y decir si existe una correlación? Si buscas tendencias en los datos, notarás que con el tiempo las exportaciones de agua han aumentado, mientras que el número de peces ha disminuido más o menos. A medida que uno sube, el otro baja, lo que es señal de una correlación negativa. Sólo un estadístico puede decir qué tan fuerte es la correlación, pero se puede decir por las tendencias que una correlación está presente y que es poco probable que se deba a fluctuaciones accidentales en los niveles de agua y peces.
1 Hemos estado usando variables discretas, no continuas; es decir, los puntos en las gráficas están desconectados. Muchas variables son continuas y no discretas, por ejemplo, el tiempo, la altitud y el grado de satisfacción con un político. Las variables continuas siempre se pueden convertir en variables discretas dividiendo el continuo en categorías separadas; por ejemplo, la variable continua tiempo podría ser reemplazada por la variable discreta tiempo hasta el minuto más cercano. La correlación entre dos variables puede realmente cuantificarse. Es decir, se puede asignar un número a la correlación. El número, llamado coeficiente de correlación, puede variar desde menos uno para una correlación negativa hasta más uno para una correlación positiva. En este capítulo, no vamos a investigar cómo calcular estos coeficientes. El coeficiente de correlación es una medida de qué tan bien representará un gráfico de línea recta los datos. Considera una gráfica que se vea así:
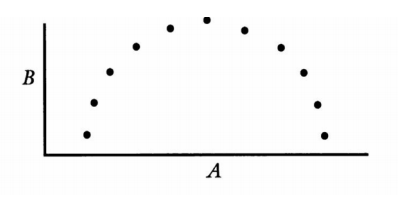
Esta gráfica tiene un coeficiente de correlación pequeño, por lo que una línea recta no hace un buen trabajo de representación de esta gráfica. Sin embargo, existe claramente algún tipo de correlación entre A y B. Es una correlación no lineal.
2 Los estadísticos prefieren usar una medida de fuerza algo más complicada para las correlaciones, pero esta definición puede ser bastante útil como regla general.


