5.5: Razonamiento Estadístico- Teorema de Bayes

Diagramas de frecuencia: Una primera mirada a Bayes

El razonamiento bayesiano trata sobre cómo revisar nuestras creencias a la luz de la evidencia. Empezaremos considerando un escenario en el que la fuerza de la evidencia tenga números claros adjuntos. (No te preocupes si no sabes cómo resolver el siguiente problema. Veremos en breve cómo resolverlo.)

Supongamos que usted es una enfermera que evalúa a un grupo de estudiantes para detectar una enfermedad llamada Diseasitis.1

• Ya sabes, de estudios poblacionales pasados, que alrededor del 20% de los estudiantes tendrán Diseasitis en esta época del año.

Estás realizando pruebas para detectar Diseasitis usando un depresor de lengua que cambia de color, que generalmente se vuelve negro si el estudiante tiene Diseasitis.

• Entre los pacientes con Diseasitis, el 90% vuelve negro el depresor lingual.
• Sin embargo, el depresor de lengua no es perfecto, y también se vuelve negro el 30% del tiempo para los estudiantes sanos.

Uno de tus alumnos entra a la oficina, toma el examen y vuelve negro el depresor de lengua. ¿Cuál es la probabilidad de que tengan Diseasitis?

(Si crees que ves cómo hacerlo, puedes intentar resolver este problema antes de continuar. Para ver rápidamente si obtuvo su respuesta correcta, puede ampliar el botón “Responder” a continuación; la derivación se dará en breve.)

La probabilidad de que un estudiante con un depresor lingual ennegrecido tenga Diseasitis es 3/7, aproximadamente 43%. Este problema se puede resolver de una manera difícil o de una manera fácil inteligente. Primero caminaremos por el camino difícil.

Primero, imaginamos una población de 100 estudiantes, de los cuales 20 tienen Diseasitis y 80 no.2

El 90% de los estudiantes enfermos se vuelven negros su depresor de lengua, y el 30% de los estudiantes sanos, el depresor de lengua se vuelve negro. Entonces vemos depresores de lengua negros en 90% * 20 = 18 estudiantes enfermos, y 30% * 80 = 24 estudiantes sanos.

¿Cuál es la probabilidad de que un estudiante con un depresor de lengua negro tenga Diseasitis? Del diagrama, hay 18 estudiantes enfermos con depresores de lengua negros. 18 + 24 = 42 estudiantes en total se volvieron negros sus depresores de lengua. Imagínese meterse en una bolsa de todos los estudiantes con depresores de lengua negros, y sacar a uno de esos alumnos al azar; ¿cuál es la posibilidad de que un estudiante así esté enfermo?

La respuesta final es que un paciente con un depresor de lengua negro tiene una probabilidad 18/42 = 3/7 = 43% de estar enfermo.

Muchos estudiantes de medicina han encontrado al principio esta respuesta contraintuitiva: ¡La prueba detecta correctamente la Diseasitis 90% de las veces! Si la prueba vuelve positiva, ¿por qué es aún menos del 50% de probabilidades de que el paciente tenga Diseasitis? Bueno, la prueba también “detecta” incorrectamente la Diseasitis 30% del tiempo en un paciente sano, y comenzamos con muchos más pacientes sanos que pacientes enfermos.

La prueba sí aporta alguna evidencia a favor de que el paciente esté enfermo. La probabilidad de que un paciente se enferme pasa de 20% antes de la prueba, a 43% después de ver que el depresor de lengua se vuelve negro. Pero esto no es concluyente, y necesitamos realizar más pruebas, quizás más costosas.

Si sientes que entiendes esta configuración del problema, considera tratar de responder la siguiente pregunta antes de continuar: ¿Cuál es la probabilidad de que un estudiante que no se vuelve negro el depresor lingual -un estudiante con un resultado negativo en la prueba- tenga Diseasitis? Nuevamente, comenzamos con 20% estudiantes enfermos y 80% sanos, 70% de los estudiantes sanos obtendrán un resultado negativo en la prueba, y solo 10% de los estudiantes enfermos obtendrán un resultado negativo en la prueba.

Imagina 20 estudiantes enfermos y 80 estudiantes sanos. 10% * 20 = 2 estudiantes enfermos tienen resultados negativos en las pruebas. 70% * 80 = 56 estudiantes sanos tienen resultados negativos en las pruebas. Entre el total de 2+56=58 estudiantes con resultados negativos en la prueba, 2 estudiantes son estudiantes enfermos con resultados negativos en la prueba. Entonces 2/58 = 1/29 = 3.4% de los estudiantes con resultados negativos en las pruebas tienen Diseasitis.

Ahora volvamos a una forma más rápida y fácil de resolver el mismo problema.

Imagina una cascada con dos corrientes de agua en la parte superior, una corriente roja y una corriente azul. Estos arroyos se acercan por separado a la cima de la cascada, con parte del agua de ambos arroyos desviándose a lo largo del camino, y el agua restante cayendo a una piscina compartida debajo.

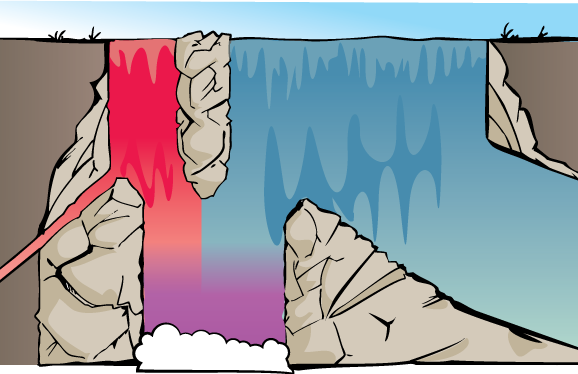
Supongamos que:

• En lo alto de la cascada, 20 galones/segundo de agua roja están fluyendo hacia abajo, y 80 galones/segundo de agua azul están bajando.
• El 90% del agua roja llega al fondo.
• El 30% del agua azul llega al fondo.

Del agua morada que llega al fondo de la alberca, ¿cuánto era originario del arroyo rojo y cuánto era originario del arroyo azul?

Esto es estructuralmente idéntico al problema de la Diseasitis de antes:

• El 20% de los pacientes de la población de tamizaje inician con Diseasitis.
• Entre los pacientes con Diseasitis, el 90% vuelve negro el depresor lingual.
• El 30% de los pacientes sin Diseasitis también volverán negro al depresor de lengua.

El 20% de los pacientes enfermos son análogos a los 20 galones/segundo de agua roja; el 80% de los pacientes sanos son análogos a los 80 galones/segundo de agua azul:

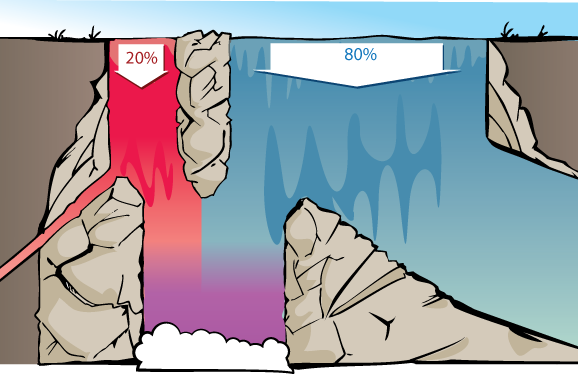
El 90% de los pacientes enfermos que se vuelven negros el depresor lingual es análogo al 90% del agua roja que llega al fondo de la cascada. El 30% de los pacientes sanos que se vuelven negros al depresor lingual es análogo al 30% del agua azul que llega a la piscina inferior.

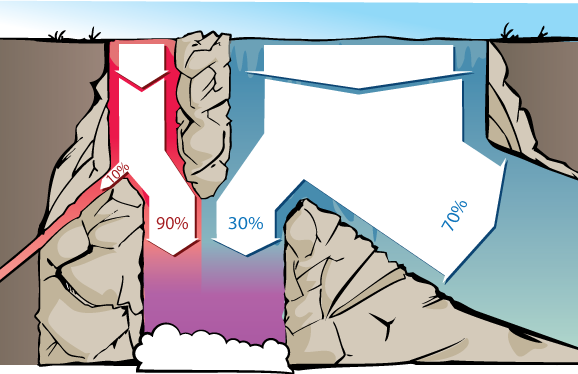
Por lo tanto, la pregunta “¿qué porción de agua en la piscina final vino del arroyo rojo?” tiene la misma respuesta que la pregunta “¿qué parte de los pacientes que se vuelven negros el depresor lingual están enfermos de Diseasitis?”

Ahora por la forma más rápida de responder a esa pregunta.

Comenzamos con 4 veces más agua azul que agua roja en la cima de la cascada.

Entonces cada molécula de agua roja tiene 90% de probabilidades de llegar a la piscina compartida, y cada molécula de agua azul tiene 30% de probabilidades de llegar a la piscina. (90% de agua roja y 30% de agua azul llegan al fondo.) Entonces cada molécula de agua roja es 3 veces más probable (0.90/0.30 = 3) que una molécula de agua azul para llegar al fondo.

Entonces multiplicamos las proporciones anteriores para rojo vs azul por probabilidades relativas de y terminamos con proporciones finales que significan que la piscina inferior tiene 3 partes de agua roja por 4 partes de agua azul.

Para convertir estas proporciones relativas en una probabilidad absoluta de que una molécula de agua aleatoria en el fondo sea roja, calculamos 3/(3 + 4) para ver que 3/7ths (aproximadamente 43%) del agua en la piscina compartida provenía del arroyo rojo.

Esta proporción es la misma que la de los 18:24 pacientes enfermos con resultados positivos, versus pacientes sanos con resultados positivos en las pruebas, que obtendríamos pensando en 100 pacientes.

Es decir, para resolver el problema de la Diseasitis en tu cabeza, podrías convertir esta palabra problema:

El 20% de los pacientes en una población de tamizaje presentan Diseasitis. El 90% de los pacientes con Diseasitis vuelven el depresor lingual negro y el 30% de los pacientes sin Diseasitis vuelven el depresor lingual negro. Dado que un paciente se volvió negro su depresor de lengua, ¿cuál es la probabilidad de que tenga Diseasitis?

Bien, entonces las probabilidades iniciales son (20%: 80%) = (1:4), y las probabilidades son (90%: 30%) = (3:1). Multiplicar esas proporciones da probabilidades finales de (3:4), que se convierte en una probabilidad de 3/7ths.

(Es posible que no puedas convertir 3/7 a 43% en tu cabeza, pero podrías ser capaz de hacer un globo ocular que era un trozo menor al 50%).

Puedes intentar hacer un cálculo similar para este problema:

• El 90% de los widgets son buenos y el 10% son malos.
• El 12% de los widgets malos emiten chispas.
• Sólo 4% de los buenos widgets emiten chispas.

¿Qué porcentaje de widgets chispeantes son malos? Si estás lo suficientemente cómodo con la configuración, intenta hacer este problema completamente en tu cabeza.

(Podrías intentar visualizar una cascada con buenos y malos widgets en la parte superior, y solo chispeando widgets que llegan a la piscina inferior).

• Hay (1:9) malos vs. buenos widgets.
• Los widgets malos vs buenos tienen una probabilidad relativa (12:4) de chispas.
• Esto simplifica a (1:9) x (3:1) = (3:9) = (1:3), 1 widget de chispas malas por cada 3 buenos widgets de chispas.
• Lo que convierte a una probabilidad de 1/ (1+3) = 1/4 = 25%; es decir, 25% de los widgets chispeantes son malos.

Ver chispas no nos hizo “creer que el widget es malo”; la probabilidad sólo fue al 25%, que es menos de 50/50. Pero esto no significa que digamos: “¡Sigo creyendo que este widget es bueno!” y arrojar las pruebas e ignorarlas. Un widget malo es relativamente más probable que emita chispas, y por lo tanto al ver esta evidencia debería hacernos pensar que es relativamente más probable que el widget sea malo, incluso si la probabilidad aún no ha superado el 50%. Aumentamos nuestra probabilidad de 10% a 25%.

Las cascadas son una forma de visualizar la “forma de probabilidades” de la “regla de Bayes”, que establece que las probabilidades previas por la razón de verosimilitud son iguales a las probabilidades posteriores. A su vez, esta regla puede verse como formalizar la noción de “la fuerza de la evidencia” o “cuánto debe hacernos actualizar nuestras creencias una pieza de evidencia”.