3.3: Respuesta Transitoria
- Page ID
- 84184
La respuesta transitoria de un elemento o sistema es su salida en función del tiempo que sigue a la aplicación de una entrada especificada. La señal de prueba elegida para excitar la respuesta transitoria del sistema puede ser una entrada que se anticipa en el funcionamiento normal, o puede ser una abstracción matemática seleccionada debido a la perspicacia que presta al comportamiento del sistema. Las señales de prueba comúnmente utilizadas incluyen las integrales de impulso y tiempo de esta función.
Selección de entradas de prueba
Las matemáticas de los sistemas lineales aseguran que la misma información del sistema sea obtenible independientemente de la entrada de prueba utilizada, ya que la función de transferencia de un sistema es claramente independiente de las entradas aplicadas al sistema. En la práctica, sin embargo, frecuentemente encontramos que ciertos aspectos del rendimiento del sistema se evalúan más fácilmente seleccionando la entrada de prueba para acentuar las características de interés.
Por ejemplo, podríamos intentar evaluar la ganancia d-c de un amplificador operativo con retroalimentación excitándolo con un impulso y midiendo el área neta bajo la respuesta de impulso del amplificador. Este enfoque es matemáticamente sólido, como lo demuestra el siguiente desarrollo. Supongamos que la función de transferencia de bucle cerrado del amplificador es\(G(s)\) y que la respuesta de impulso correspondiente [la transformada inversa de\(G(s)\)] es\(g(t)\). Las propiedades de las transformadas de Laplace muestran que
\[\int_{0}^{t} g(t) dt = \dfrac{1}{s} G(s) \nonumber \]
El teorema del valor final aplicado a esta función indica que el área neta bajo respuesta al impulso es
\[\lim_{t \to \infty} \int_{0}^{t} g(t) \ dt = \lim_{s \to 0} s \dfrac{1}{s} G(s) = G(0) \nonumber \]
Desafortunadamente, esta técnica implica trampas experimentales. El primero de ellos es la elección de la función de tiempo utilizada para aproximar un impulso. Para que un pulso de duración finita se aproxime satisfactoriamente a un impulso, es necesario tener (Si bien esta afirmación es cierta en general, si solo se requiere la ganancia d-c del sistema, se puede utilizar cualquier pulso. Una extensión del desarrollo anterior muestra que el área bajo la respuesta a cualquier entrada de unidad de área es idéntica al área bajo la respuesta de impulso.)
\[t_p \ll \dfrac{1}{|s_m|} \nonumber \]
donde\(t_p\) está el ancho del pulso y\(s_m\) es la frecuencia del polo del\(G(s)\) que se encuentra más alejado del origen.
Puede ser difícil encontrar un generador de pulsos que produzca pulsos lo suficientemente estrechos como para probar amplificadores de alta frecuencia. Además, el pulso estrecho frecuentemente conduce a una salida de pequeña amplitud con problemas de medición asociados. Incluso si se obtiene una respuesta de impulso satisfactoria, la tediosa tarea de integrar esta respuesta (posiblemente contando cajas bajo la pantalla de salida en un osciloscopio) permanece. Debe ser evidente que una medición mucho más precisa y directa de la ganancia d-c es posible si se aplica una entrada constante al amplificador.
Alternativamente, los componentes de alta frecuencia de la respuesta del sistema no se excitan significativamente si se aplican entradas que varían lentamente en el tiempo como entradas de prueba. De hecho, los sistemas pueden tener polos de alta frecuencia cerca del eje imaginario en el\(s\) plano, y así bordear la inestabilidad; sin embargo, exhiben salidas de buen comportamiento cuando se prueban con entradas que varían lentamente.
Para los sistemas que no tienen ni un polo de frecuencia cero ni un cero en su función de transferencia, la respuesta escalonada a menudo proporciona la evaluación más significativa del rendimiento. La ganancia d-c se puede obtener directamente midiendo el valor final de la respuesta a un paso unitario, mientras que la característica de discontinuidad inicial de un escalón excita los polos de alta frecuencia en la función de transferencia del sistema. Aproximaciones adecuadas a un paso ideal son proporcionadas por pulsos rectangulares con tiempos de subida
\[t_r \ll \dfrac{1}{|s_m|} \nonumber \]
(\(s_m\)como se definió anteriormente) y anchuras
\[t_{\omega} \gg \dfrac{1}{|s_n|} \nonumber \]
donde\(s_n\) se encuentra la frecuencia del polo en la función de transferencia ubicada más cercana al origen. Los generadores de pulsos con tiempos de subida inferiores a 1 ns están disponibles, y estos generadores pueden proporcionar información útil sobre amplificadores con anchos de banda del orden de 100 MHz.
Aproximación de respuestas transitorias
Ejemplos en la Sección 3.1 indicaron que en algunos casos es posible aproximar la respuesta transitoria de un sistema complejo utilizando la de un sistema mucho más simple. Este tipo de aproximación es posible siempre que la función de transferencia de interés esté dominada por uno o dos polos.
Considere un amplificador con una función de transferencia
\[\dfrac{V_o (s)}{V_i (s)} = \dfrac{a_0 \prod_{i = 1}^{m} (\tau_{zi} s + 1)}{\prod_{j = 1}^{n} (\tau_{pj} s + 1)} \ n > m, \text{ all } \tau > 0 \nonumber \]
La respuesta de este sistema a una entrada unidad-paso es
\[v_o (t) = \mathcal{L}^{-1} \left [\dfrac{1}{s} \dfrac{V_o(s)}{V_i (s)} \right ] = a_o + \sum_{k = 1}^{n} A_k e^{-t/\tau_p k} \nonumber \]
Las\(A\)'s obtenidas de la Ecuación 3.2.6 después de un ligero reordenamiento son
\[A_k = -a_0 \dfrac{\prod_{i = 1}^{m} \left (-\dfrac{\tau_{zi}}{\tau_{pk}} + 1 \right )}{\prod_{j = 1,j \ne k}^{n} \left (-\dfrac{\tau_{pj}}{\tau_{pk}} + 1 \right )} \label{eq3.3.8} \]
Supongamos que\(\tau_{p_1} \gg\) todas las demás r. En este caso, que corresponde a que un polo en la función de transferencia del sistema esté mucho más cerca del origen que todas las demás singularidades, la Ecuación se\(\ref{eq3.3.8}\) puede utilizar para mostrar eso\(A_1 \simeq a_0\) y todos los demás\(A\)\(\simeq 0\) para que
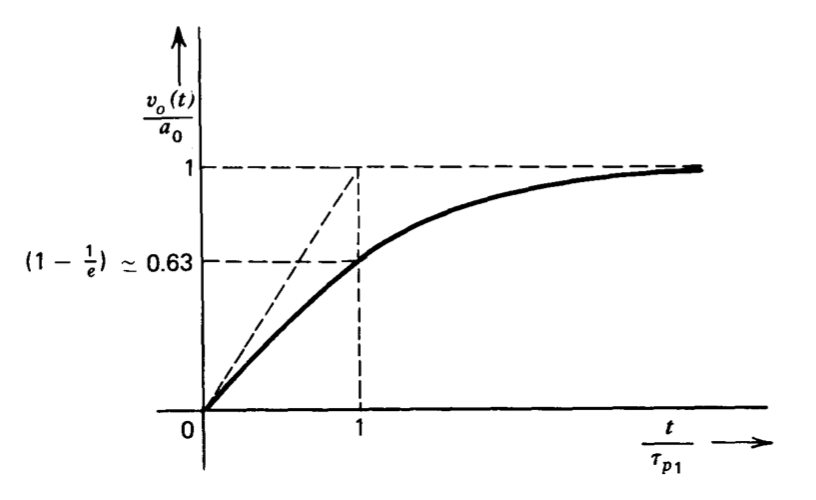
\[v_o (t) \simeq a_0 (1 - e^{-t/\tau_{p_1}}) \nonumber \]
Esta respuesta transitoria exponencial simple se muestra en la Figura 3.6. La experiencia muestra que la respuesta unipolar es una buena aproximación a la respuesta real si las singularidades remotas son un factor de cinco más lejos del origen que el polo dominante.
El resultado aproximado dado anteriormente se mantiene incluso si algunas de las singularidades remotas ocurren en pares conjugados complejos, siempre que los pares se localicen a distancias mucho mayores del origen en el\(s\) plano que el polo dominante. Sin embargo, si la parte real del par complejo no es más negativa que la ubicación del polo dominante, las sinusoides amortiguadas de pequeña amplitud y alta frecuencia pueden persistir después de que se complete el transitorio dominante.
Otro patrón de singularidad común incluye un par complejo de polos mucho más cercanos al origen en el\(s\) plano que todos los demás polos y ceros. Un argumento similar al dado anteriormente muestra que la función de transferencia de un amplificador con este tipo de patrón de singularidad puede aproximarse solo por el par complejo, y puede escribirse en forma estándar
\[\dfrac{V_o (s)}{V_i (s)} = \dfrac{a_o}{s^2/\omega_n^2 + 2 \zeta s/\omega_n + 1}\label{eq3.3.10} \]
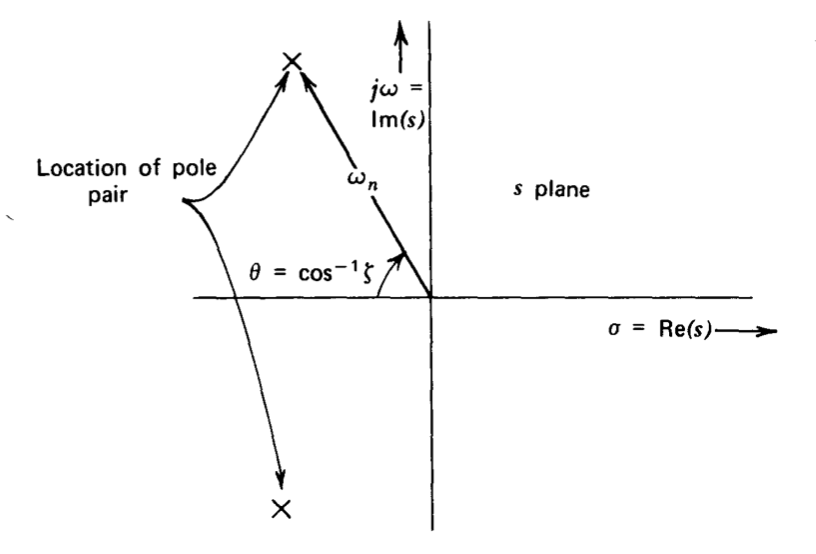
Los parámetros de la ecuación\(\omega_n\) y se\(\zeta\) denominan la frecuencia natural (expresada en radianes por segundo) y la relación de amortiguación, respectivamente. La significación física de estos parámetros se indica en la gráfica\(s\) -plano mostrada como Figura 3.7. Las ubicaciones relativas de los polos que se muestran en este diagrama corresponden a la caja subamortiguada (\(\zeta < 1\)). Otras dos posibilidades son el par amortiguado críticamente (\(\zeta = 1\)) donde los dos polos coinciden en el eje real y el caso sobreamortiguado (\(\zeta > 1\)) donde los dos polos están separados en el eje real. El polinomio denominador se puede factorizar en dos raíces con coeficientes reales para los dos últimos casos y, como resultado, normalmente no\(\ref{eq3.3.10}\) se usa la forma mostrada en Ecuación. La salida proporcionada por el amplificador descrito por la Ecuación\(\ref{eq3.3.10}\) en respuesta a un paso unitario es (de la Tabla 3.1).
\[v_o (t) = a_0 \left [1 - \dfrac{1}{\sqrt{1 - \zeta^2}} e^{-\zeta \omega_n t} \sin (\sqrt{1 - \zeta^2} \omega_n t + \Phi) \right ] \nonumber \]
donde
\[\Phi = \tan^{-1} \left [\dfrac{\sqrt{1 - \zeta^2}}{\zeta} \right ] \nonumber \]
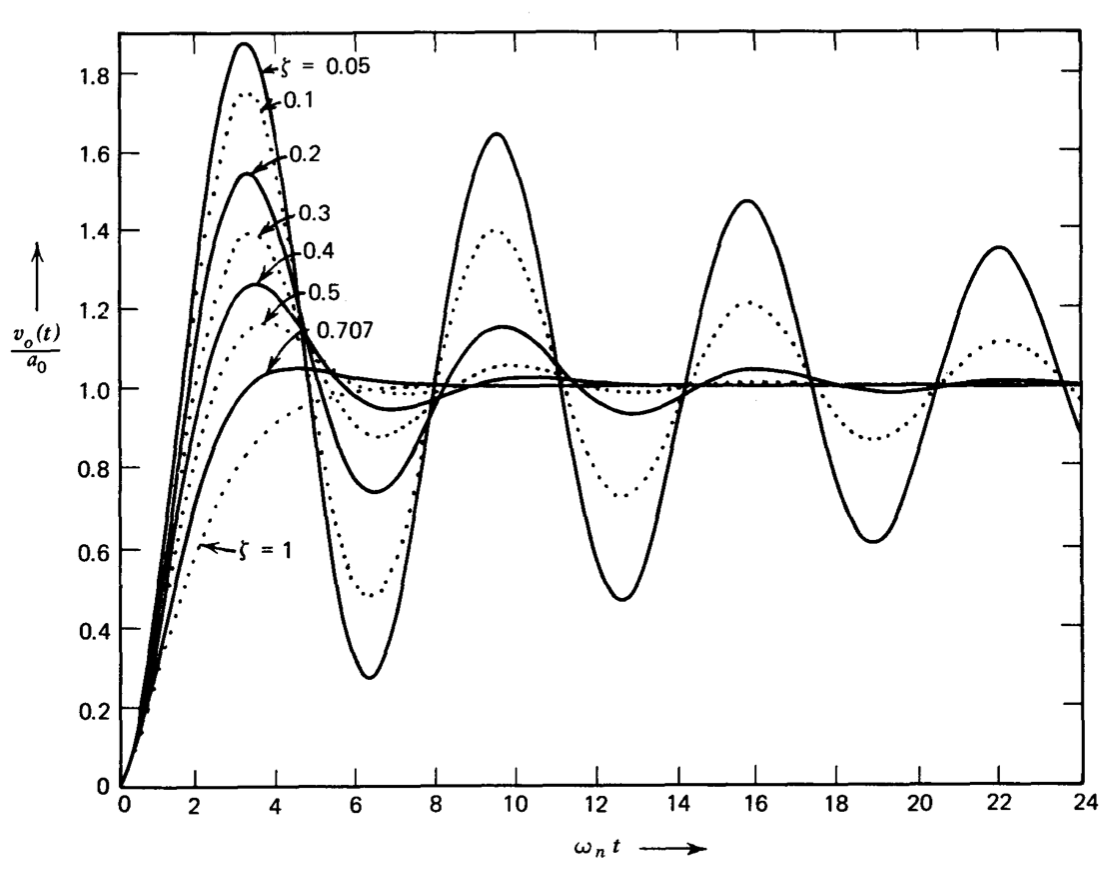
La Figura 3.8 es una gráfica de\(v_o (t)\) como función del tiempo normalizado wat para diversos valores de relación de amortiguación. Las relaciones de amortiguación más pequeñas, correspondientes a pares de polos com plex con los polos más cercanos al eje imaginario, están asociadas con respuestas escalonadas que tienen un mayor grado de sobreimpulso.
Las respuestas transitorias de los sistemas de tercer y superior orden no se categorizan tan fácilmente como las de los sistemas de primer y segundo orden, ya que se requieren más parámetros para diferenciar entre las diversas posibilidades. La situación se simplifica si las posiciones de polo relativas caen en ciertos patrones. Una clase de funciones de transferencia de interés son los filtros Butterworth. Estas funciones de transferencia también se denominan máximamente planas debido a las propiedades de sus respuestas de frecuencia (ver Sección 3.4). Las respuestas escalonadas de los filtros Butterworth también exhiben un sobreimpulso bastante bajo, y debido a estas propiedades, los amplificadores de retroalimentación a veces se compensan para que sus polos de bucle cerrado formen una configuración Butterworth.
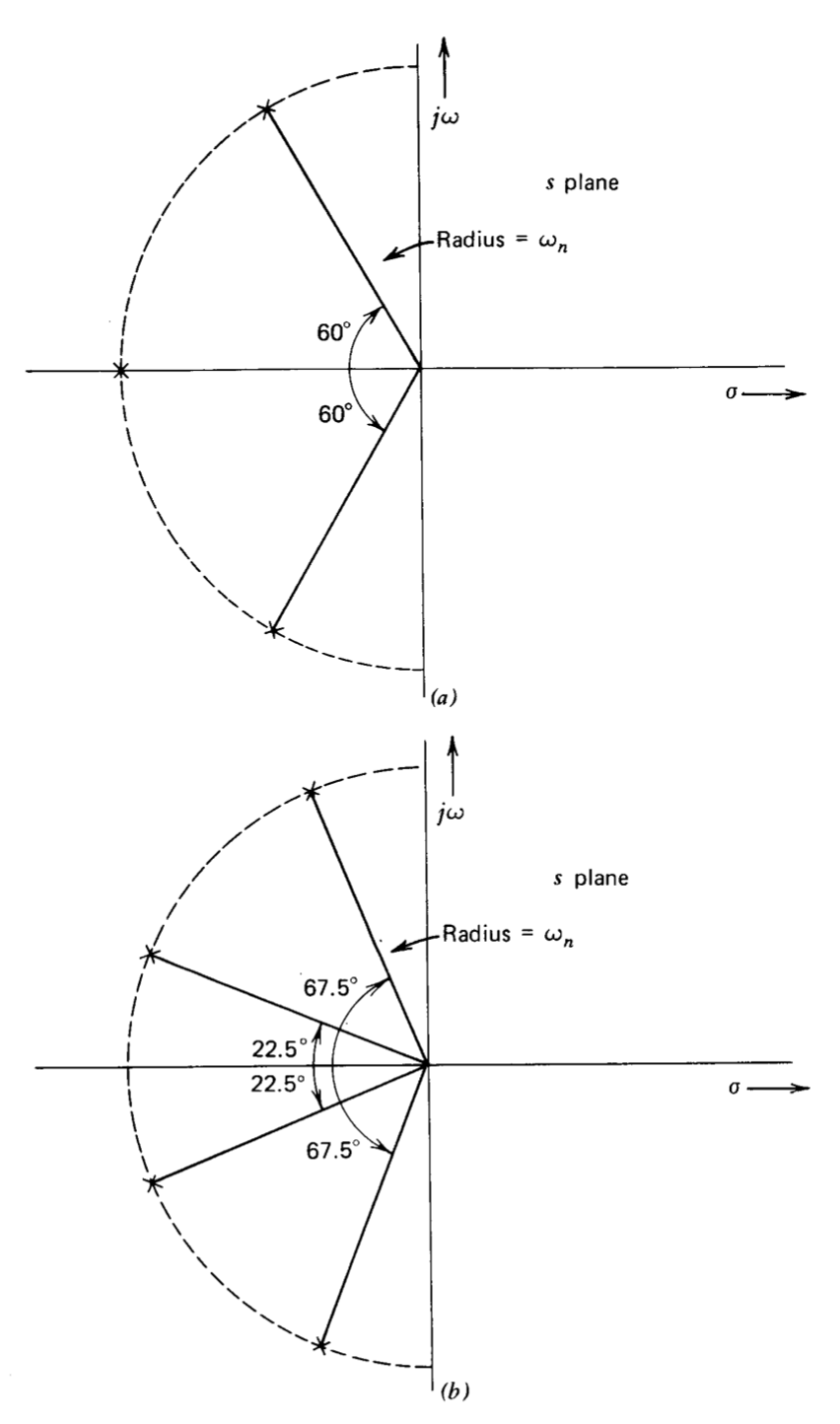
Los polos de un filtro Butterworth de orden n se encuentran en un círculo centrado en el origen del\(s\) plano. Para\(n\) par, los polos hacen ángulos\(\pm (2k + 1) 90^{\circ}/n\) con el eje real negativo, donde k toma todos los valores integrales posibles de 0 a\((n/2) - 1\). Para\(n\) impar, un polo se ubica en el eje real negativo, mientras que otros hacen ángulos de\(\pm k (180^{\circ}/n)\) con el eje real negativo donde\(k\) toma valores integrales de 1 a\((n/2) - (1/2)\). Así, por ejemplo, un filtro Butterworth de primer orden tiene un solo polo ubicado en\(s = - \omega_n\). El filtro Butterworth de segundo orden tiene sus polos ubicados\(\pm 45^{\circ}\) desde el eje real negativo, lo que corresponde a una relación de amortiguación de 0.707.
Las funciones de transferencia para filtros Butterworth de tercer y cuarto orden son
\[B_3 (s) = \dfrac{1}{s^3/\omega_n^3 + 2s^2/\omega_n^2 + 2s/\omega_n + 1} \nonumber \]
y
\[B_3 (s) = \dfrac{1}{s^4/\omega_n^4 + 2.61 s^3/\omega_n^3 + 3.42 s^2/\omega_n^2 + 2.61 s/\omega_n + 1} \nonumber \]
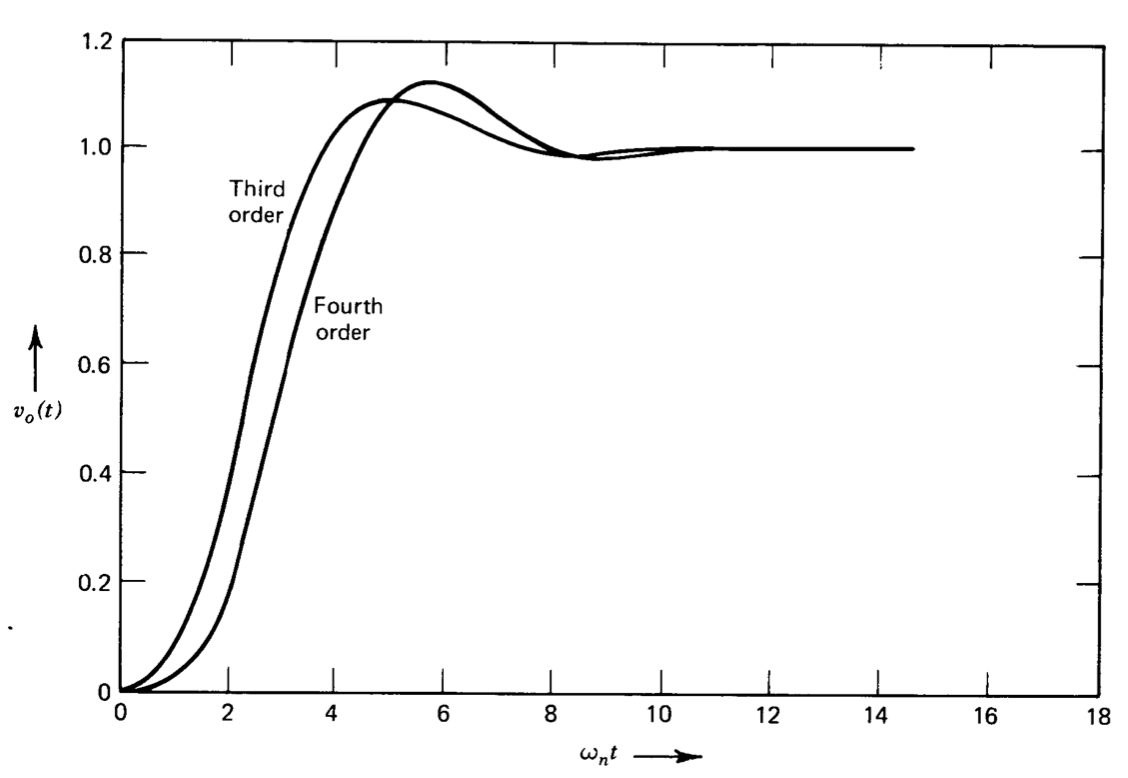
respectivamente. Las gráficas de las ubicaciones de los polos de estas funciones se muestran en la Figura 3.9. Las salidas transitorias de estos filtros en respuesta a los pasos unitarios se muestran en la Figura 3.10.
