3.4: Respuesta de frecuencia
- Page ID
- 84185
La respuesta de frecuencia de un elemento o sistema es una medida de su desempeño en estado estacionario bajo condiciones de excitación sinusoidal. En estado estacionario, la salida de un elemento lineal excitado con una sinusoide a una frecuencia\(\omega\) (expresada en radianes por segundo) es puramente sinusoidal a frecuencia\(\omega\). La respuesta de frecuencia se expresa como una ganancia o magnitud\(M(\omega)\) que es la relación de la amplitud de la salida a la sinusoide de entrada y un ángulo de fase\(\phi (\omega)\) que es el ángulo relativo entre las sinusoides de salida y entrada. El ángulo de fase es positivo si la salida conduce la entrada. Los dos componentes que comprenden la respuesta de frecuencia de un sistema con una función de transferencia\(G(s)\) vienen dados por
\[M(\omega) = |G(j\omega)| \nonumber \]
\[\phi (\omega) = \measuredangle G(j \omega) = \tan^{-1} \dfrac{\text{Im} [G(j\omega)]}{\text{Re} [G(j\omega)]} \nonumber \]
Frecuentemente es necesario determinar la respuesta de frecuencia de un sistema con una función de transferencia que es una relación de polinomios en\(s\). Un método posible es evaluar la respuesta de frecuencia sustituyendo\(j\omega\)\(s\) en todas las frecuencias de interés, pero este método es engorroso, particularmente para polinomios de alto orden. Un enfoque alternativo es presentar gráficamente la formación relativa a la respuesta de frecuencia, como se describe a continuación.
La función de transferencia se factoriza primero de manera que tanto el numerador como el denominador consten de productos de términos de primer y segundo orden con coeficientes reales. La función puede entonces ser escrita en la forma general
\[\begin{array} {rcl} {G(s)} & = & {\dfrac{a_0}{s^n} \left [\prod_{\text{first-order zeros}} (\tau_h s + 1)\right ] \left [\prod_{\text{complex zero pairs}} \left (\dfrac{s^2}{\omega_{ni}^2} + \dfrac{2\zeta_i s}{\omega_{ni}} + 1 \right )\right ]} \\ {} & \ & {\times \left [\prod_{\text{first-order poles}} \dfrac{1}{(\tau_j s + 1)}\right ] \left [\prod_{\text{complex pole pairs}} \dfrac{1}{(s^2/\omega_{nk}^2 + 2 \zeta_k s/\omega_{nk} + 1)}\right ]} \end{array}\label{eq3.4.3} \]
Mientras que varios métodos como el método de Lin (S. N. Lin, “Un método de aproximaciones sucesivas de evaluación de las raíces reales y com plex de ecuaciones cúbicas y de orden superior”, J. Math. Phys., Vol. 20, No. 3, agosto de 1941, pp. 231-242.) están disponibles para factorizar polinomios, esta operación puede ser tediosa a menos que se emplee computación de máquina, particularmente cuando el orden del polinomio es grande. Afortunadamente, en muchos casos de interés los polinomios son de orden bajo o están disponibles en las ecuaciones del sistema en forma factorizada.
Dado que\(G(j \omega)\) es una función de una variable compleja, su ángulo\(\phi (\omega)\) es la suma de los ángulos de los términos constituyentes. De igual manera, su magnitud\(M(\omega)\) es producto de las magnitudes de los componentes. Además, si las magnitudes de los componentes se trazan en una escala logarítmica, el log de\(M\) viene dado por la suma de los registros correspondientes a los componentes individuales. (El decibelio, igual a 20 logio [magnitud] se utiliza a menudo para estas manipulaciones. Este uso es técnicamente correcto solo si se consideran ganancias de voltaje o ganancias de corriente entre partes de un circuito con niveles de impedancia idénticos. El tema se confunde aún más cuando el decibelio se utiliza indiscriminadamente para expresar cantidades dimensionadas como las transconductancias. Normalmente reservaremos este tipo de presentación para manipulaciones de transmisión de bucle (la transmisión de bucle de cualquier sistema de retroalimentación debe ser adimensional), y simplemente trazaremos relaciones de señal en coordenadas logarítmicas).
El trazado se simplifica al reconocer que solo son posibles cuatro tipos de términos en la representación de Ecuación\(\ref{eq3.4.3}\):
- Constantes,\(a_0\).
- Diferenciaciones o integraciones de orden único o múltiple\(s^n\), donde\(n\) pueden ser positivas (diferenciaciones) o negativas (integraciones).
- Términos de primer orden\((\tau s + 1)\), o su recíproco.
- Pares conjugados complejos\(s^2 / \omega_n^2 + 2 \zeta s /\omega_n + 1\), o su recíproco.
Es particularmente conveniente representar cada uno de estos términos posibles como una gráfica de\(M\) (en una escala de magnitud logarítmica) y\(\phi\) (expresada en grados) en función de o (expresado en radianes por segundo) trazada en un eje de frecuencia logarítmica. Se utiliza un eje de frecuencia logarítmica porque proporciona una resolución adecuada en los casos en que el rango de frecuencia de interés es amplio y porque la forma relativa de una curva de respuesta particular en el eje logarítmico no cambia a medida que se escala en frecuencia. La magnitud y el ángulo de cualquier función racional se pueden determinar entonces sumando las magnitudes y ángulos de sus componentes. Esta representación de la respuesta de frecuencia de un sistema o elemento se denomina gráfica Bode.
La magnitud de un término ao es simplemente una constante independiente de la frecuencia, con un ángulo igual\(0^{\circ}\) o\(180^{\circ}\) dependiendo de si el signo de ao es positivo o negativo, respectivamente.
Tanto las diferenciaciones como las integraciones son posibles en los sistemas de retroalimentación. Por ejemplo, un filtro de paso alto de primer orden tiene un solo cero en el origen y, por lo tanto, su relación de transferencia de voltaje incluye un factor\(s\). Un motor (frecuentemente utilizado en sistemas de retroalimentación mecánica) incluye un factor\(1/s\) en la función de transferencia que relaciona el ángulo mecánico del eje con el voltaje aplicado del motor, ya que un voltaje de entrada constante provoca una rotación ilimitada del eje. De igual manera, diversos tipos de detectores de fase son ejemplos de elementos puramente electrónicos que tienen un polo en el origen en sus funciones de transferencia. Este polo resulta ser causa que el voltaje fuera de dicho circuito es proporcional a la diferencia de ángulo de fase entre dos señales de entrada, y este ángulo es igual a la integral de la diferencia de frecuencia entre las dos señales. También veremos que a menudo es conveniente aproximar la función de transferencia de un amplificador con alta ganancia d-c y un solo polo de baja frecuencia como integración.
La magnitud de un término\(s^n\) es igual a\(\omega^n\), una función que pasa por 1 at\(\omega = 1\) y tiene una pendiente de\(n\) en coordenadas logarítmicas. El ángulo de esta función está\(n \times 90^{\circ}\) en todas las frecuencias.
La magnitud de un polo de primer orden\(1/(\tau s + 1)\) es
\[M = \dfrac{1}{\sqrt{\tau^2 \omega^2 + 1}} \nonumber \]
mientras que el ángulo de esta función es
\[\phi = -\tan^{-1} \tau \omega \nonumber \]
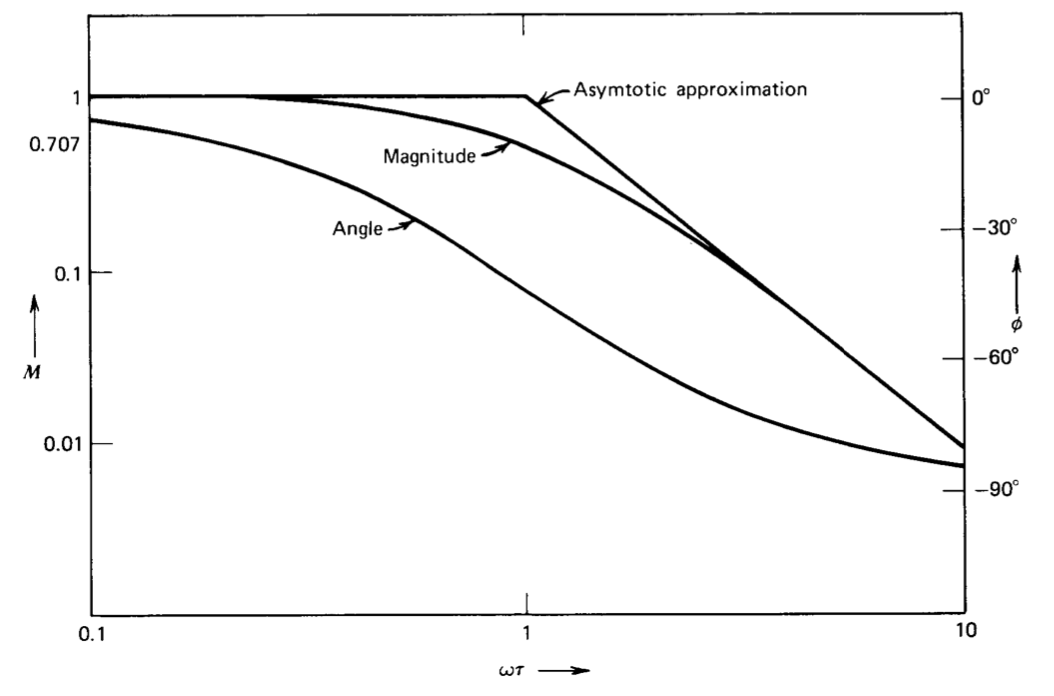
La magnitud y el ángulo para el polo de primer orden se representan en función de la frecuencia normalizada en la Figura 3.11. Una característica esencial de la función de magnitud es que se puede aproximar por dos líneas rectas, una que se extiende a lo largo de la\(M = 1\) línea y la otra con una pendiente de -1, que se cruzan en\(\omega = 1/\tau\). (Esta frecuencia se llama frecuencia de esquina.) La desviación máxima de las curvas reales de la representación asintótica es un factor de 0.707 y ocurre en la frecuencia de esquina. La magnitud y el ángulo para un cero de primer orden se obtienen invirtiendo las curvas mostradas para el polo, de manera que la magnitud se aproxime a una pendiente asintótica de +1 más allá de la frecuencia de esquina, mientras que el ángulo cambia de 0 a +\(90^{\circ}\).
La magnitud de un par de polos complejo-conjugado
\[\dfrac{1}{s^2 / \omega_n^2 + 2 \zeta s/ \omega_n + 1}\nonumber \]
es
\[M = \dfrac{1}{\sqrt{\dfrac{4\zeta^2 \omega^2}{\omega_n^2} + \left (1 - \dfrac{\omega^2}{\omega_n^2} \right )^2}} \nonumber \]
con el ángulo correspondiente
\[\phi = -\tan^{-1} \dfrac{2 \zeta \omega /\omega_n}{1 - \omega^2 /\omega_n^2} \nonumber \]
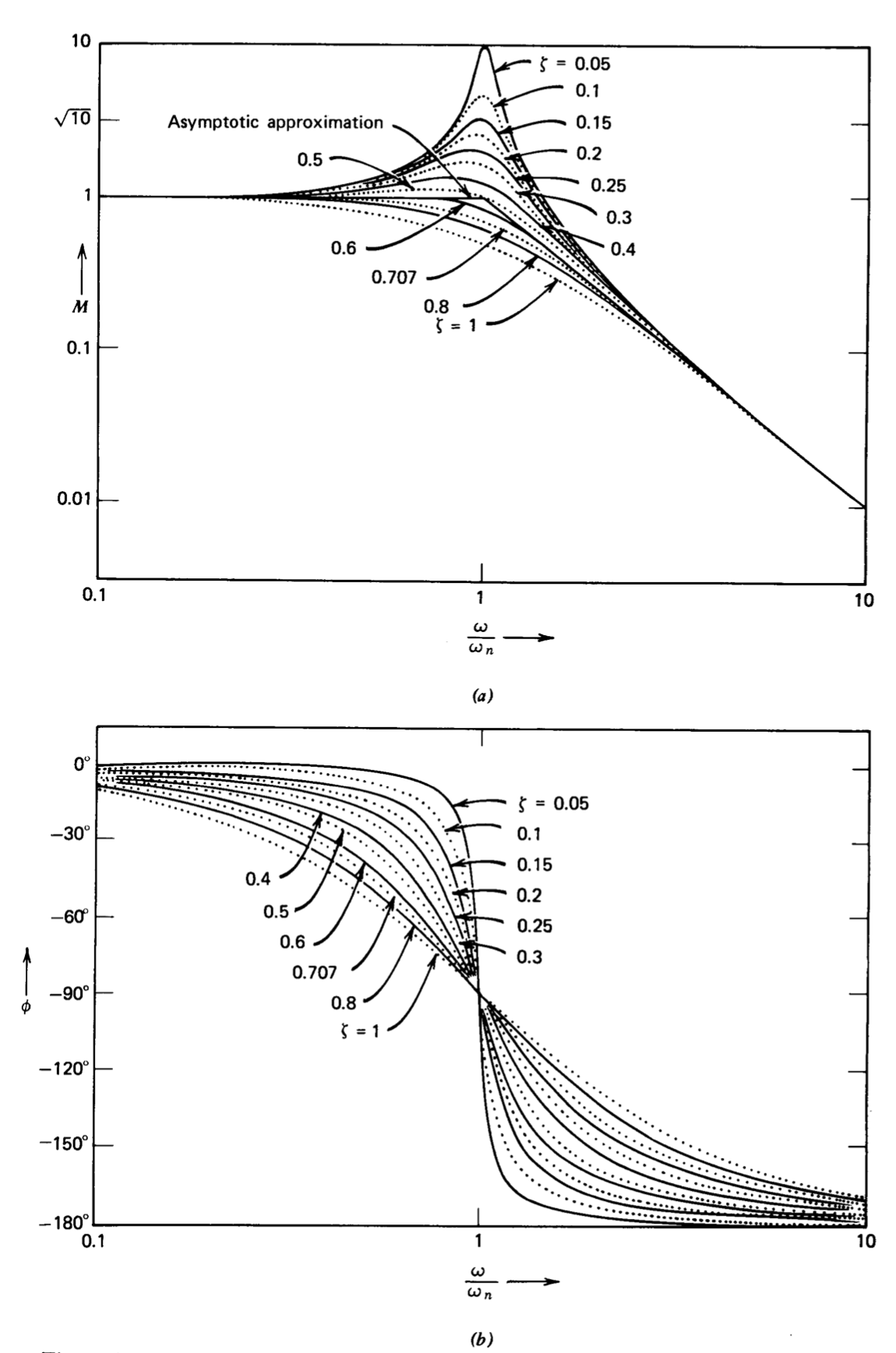
Estas funciones se muestran en forma Bode-plot como una familia paramétrica de curvas trazadas frente a la frecuencia normalizada\(\omega / \omega_n\) en la Figura 3.12. Tenga en cuenta que la aproximación asintótica a la magnitud es razonablemente precisa siempre que la relación de amortiguación supere 0.25. Las curvas correspondientes para un cero complejo-conjugado se obtienen invirtiendo las curvas mostradas en la Figura 3.12.
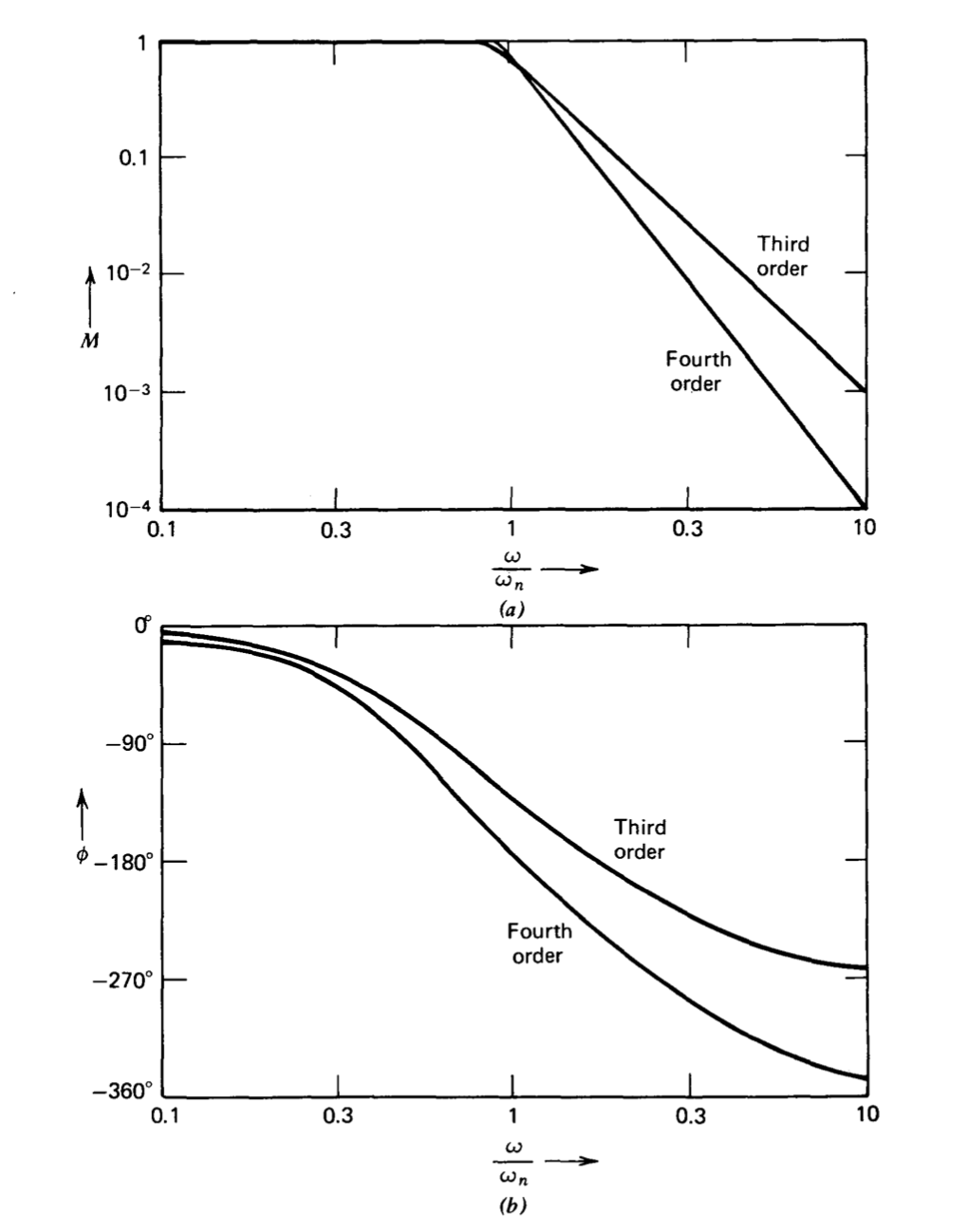
Se afirmó en la Sección 3.3.2 que los amplificadores de retroalimentación ocasionalmente se ajustan para tener respuestas de Butterworth. Las respuestas de frecuencia para los filtros Butterworth de tercer y cuarto orden se muestran en forma de diagrama de Bodes en la Figura 3.13. Tenga en cuenta que no hay pico en la respuesta de frecuencia de estos
funciones de transferencia máxima plana. También vemos en la Figura 3.12 que la relación de amortiguación de 0.707, correspondiente a la configuración de Butterworth bipolar, divide las respuestas de segundo orden que alcanzan su pico de aquellas que no. El lector debe recordar que la planitud de la respuesta de Butterworth se refiere a su respuesta de frecuencia, y que las respuestas escalonadas de todos los filtros Butterworth exhiben sobreimpulso.
El valor asociado a las parcelas de Bode proviene en gran parte de la facilidad con la que se puede obtener la parcela para un sistema complejo. La función general de transferencia del sistema se puede obtener mediante el siguiente procedimiento. Primero, se trazan las curvas de magnitud y fase correspondientes a todos los términos incluidos en la función de transferencia de interés. Cuando se utilizan las curvas de primer y segundo orden (Figs. 3.11 y 3.12), se ubican a lo largo del eje de frecuencia de manera que sus frecuencias de esquina corresponden a las de los factores representados. Una vez trazadas estas curvas, la magnitud de la función de transferencia completa a cualquier frecuencia se obtiene sumando las distancias lineales desde la magnitud unitaria de todos los componentes a la frecuencia de interés. Se puede utilizar el mismo tipo de adición gráfica para obtener la curva de fase completa. Divisores, o ayudas similares, se pueden utilizar para por forma la adición gráfica.
En la práctica, la curva de magnitud asintótica generalmente se esboza dibujando una serie de líneas rectas que se cruzan con cambios de pendiente apropiados en las intersecciones. Las correcciones a la curva asintótica se pueden agregar en las proximidades de singularidades si es necesario.
La información contenida en una parcela de Bode también se puede presentar como una gráfica de fase de ganancia, que es una representación más conveniente para algunas operaciones. Se utilizan coordenadas rectangulares, representando la ordenada la magnitud (en una escala logarítmica) y la abscisa representando el ángulo de fase en grados. La frecuencia expresada en radianes por segundo es un parámetro a lo largo de la curva de ganancia-fase. Las gráficas de fase de ganancia se dibujan frecuentemente transfiriendo datos de una gráfica de Bode.
La función de transferencia
\[G(s) = \dfrac{10^7(10^{-4} + 1)}{s(0.01s + 1) (s^2/10^{12} + 2 (0.2) s/ 10^6 + 1)} \nonumber \]
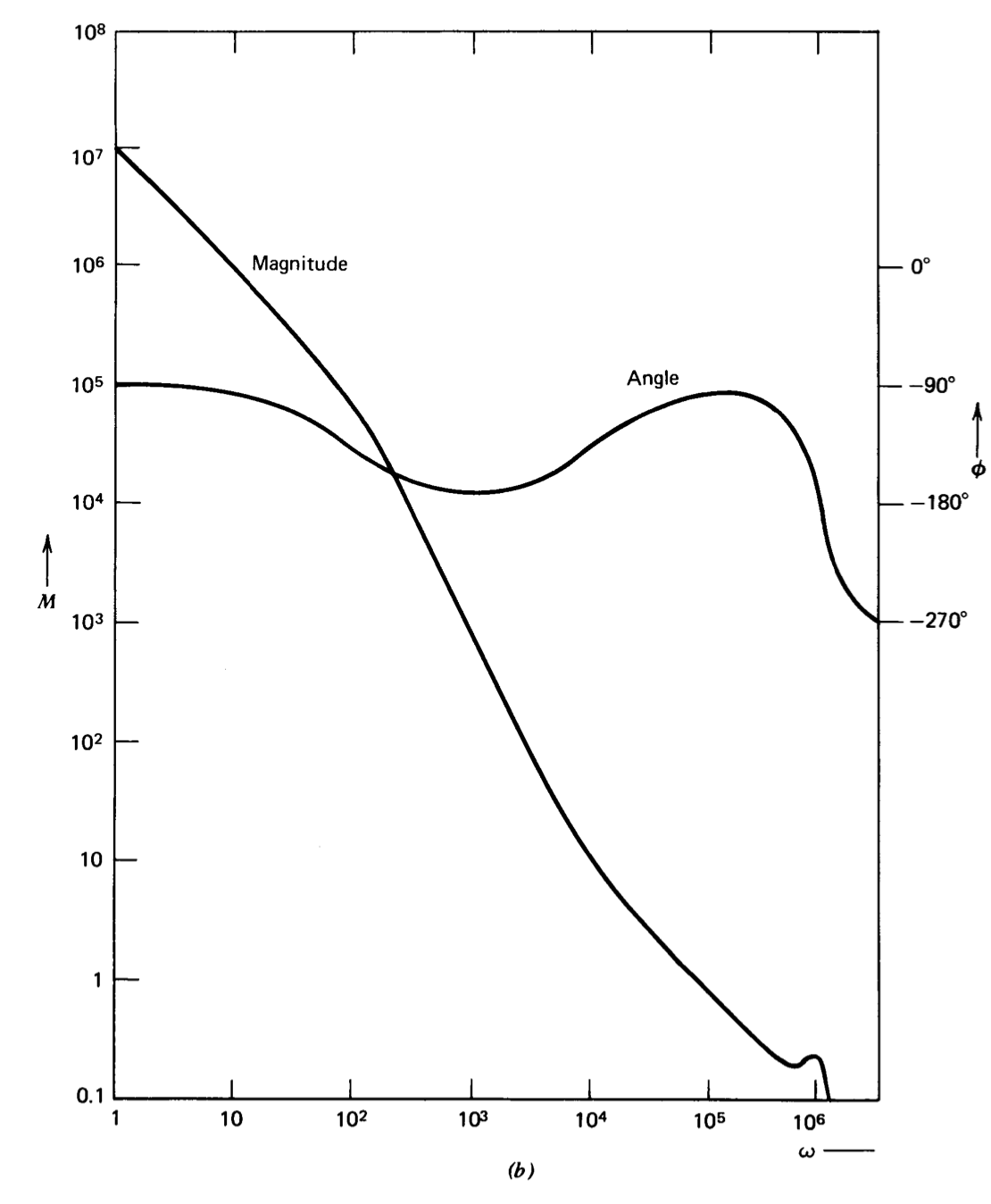
se utiliza para ilustrar la construcción de parcelas Bode y fase de ganancia. Esta función incluye estos cinco factores:
- Una constante\(10^7\).
- Una sola integración.
- Un polo de primer orden con una constante de tiempo de 0.01 segundos, correspondiente a una frecuencia de esquina de 100 radianes por segundo.
- Un cero de primer orden con una constante de tiempo de\(10^{-4}\) segundos, correspondiente a una frecuencia de esquina de\(10^4\) radianes por segundo.
- Un par de polos complejo-conjugado con una frecuencia natural de\(10^6\) radianes por segundo y una relación de amortiguación de 0.2.
Los factores individuales se muestran en forma de Bode-plot en una escala de frecuencia común en la Figura 3.14\(a\). Estos factores se combinan para producir la gráfica Bode para la función de transferencia completa en la Figura 3.14\(b\). La misma información se presenta en forma de fase de ganancia en la Figura 3.15.


