4.2: EL CRITERIO DE RUTA
- Page ID
- 84104
La prueba de Routh es un método matemático que puede utilizarse para determinar el número de ceros de un polinomio con partes reales positivas. Si la prueba se aplica al polinomio denominador de una función de transferencia (también llamada ecuación característica) la ausencia de ceros de medio plano derecho de la ecuación característica garantiza la estabilidad del sistema. Una ventaja computacional de la prueba de Routh es que no es necesario factorizar el polinomio para aplicar la prueba.
Evaluación de Estabilidad
Se describe la prueba para un polinomio de la forma
\[P(s) = a_0 s^n + a_1 s^{n - 1} + \cdots + a_{n - 1} s + a_n \label{eq4.2.1} \]
Una condición necesaria pero no suficiente para que todos los ceros de Ecuación\(\ref{eq4.2.1}\) tengan partes reales negativas es que todos los\(a\)'s estén presentes y que todos tengan el mismo signo. Si se cumple esta condición necesaria, se genera una matriz de números a partir de las a de la siguiente manera. (Este ejemplo es para\(n\) par. Para\(n\) impar,\(a_n\) termina la segunda fila.)
\[\begin{array} {ccccccc} {a_0} & {a_2} & {a_4} & \cdot & \cdot & {a_{n - 2}} & {a_n} \\ {a_1} & {a_3} & {a_5} & \cdot & \cdot & {a_{n - 1}} & {0} \\ {\dfrac{a_1 a_2 - a_0 a_3}{a_1} = b_1} & {\dfrac{a_1 a_4 - a_0 a_5}{a_1} = b_2} & {\cdot} & \cdot & \cdot & {\dfrac{a_1 a_n - a_0 \cdot 0}{a_1} = b_{n/2}} & {0} \\ {\dfrac{b_1 a_3 - a_1 b_2}{b_1} = c_1} & {\dfrac{b_1 a_5 - a_1 b_3}{b_1} = c_2} & {\cdot} & \cdot & \cdot & {0} & {0} \\ {\dfrac{c_1 b_2 - b_1 c_2}{c_1} = d_1} & {\cdot} & {\cdot} & \cdot & \cdot & {0} & {0} \\ {\cdot} & {\cdot} & {\cdot} & \cdot & \cdot & {\cdot} & {\cdot} \\ {\cdot} & {\cdot} & {\cdot} & \cdot & \cdot & {\cdot} & {\cdot} \\ {0} & {0} & {\cdot} & \cdot & \cdot & {0} & {0} \end{array} \nonumber \]
A medida que se desarrolla la matriz, progresivamente más elementos de cada fila se convierten en cero, hasta que solo el primer elemento de la\(n + 1\) fila es distinto de cero. El número total de cambios de signo en la primera columna es entonces igual al número de ceros del polinomio original que se encuentran en el plano de la mitad derecha.
El uso del criterio Routh se ilustra utilizando el polinomio
\[P(s) = s^4 + 9s^3 + 14s^2 + 266s + 260\label{eq4.2.3} \]
Dado que todos los coeficientes son reales y positivos, se cumple la condición necesaria para que todas las raíces de la Ecuación\(\ref{eq4.2.3}\) tengan partes reales negativas. La matriz es
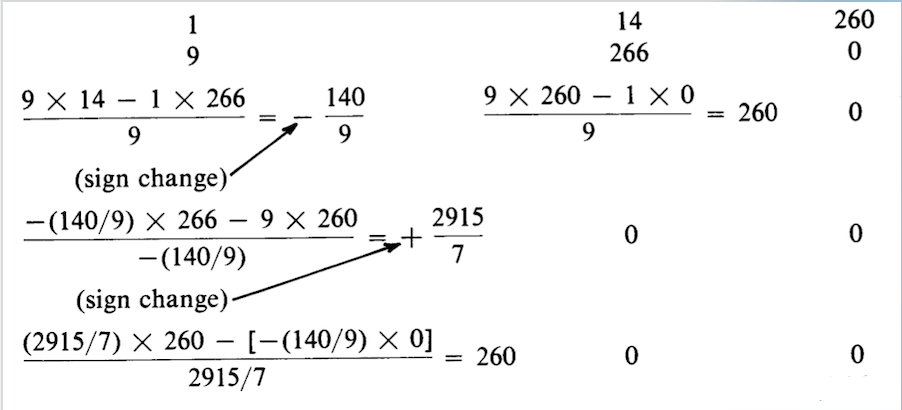
Los dos cambios de signo en la primera columna indican dos ceros de medio plano derecho. Este resultado se puede verificar factorizando el polinomio original, demostrando que
\[s^4 + 9s^3 + 14s^2 + 266s + 260 = (s - 1 + j5)(s - 1 - j5) (s + 1)(s + 10) \nonumber \]
Un segundo ejemplo es proporcionado por el polinomio
\[P(s) = s^4 + 13s^2 + 58 s^2 + 306 s+ 260 \nonumber \]
La matriz correspondiente es
\[\begin{array} {ccc} {1} & {58} & {260} \\ {13} & {306} & {0} \\ {\dfrac{13 \times 58 - 1 \times 306}{13} = \dfrac{448}{13}} & {\dfrac{13 \times 260 - 1 \times 0}{13} = 260} & {0} \\ {\dfrac{(448/13) \times 306 - 13 \times 260}{448/13} = \dfrac{23287}{112}} & {0} & {0} \\ {\dfrac{(23287/112) \times 260 - (448/13) \times 0}{23287/112} = 260} & {0} & {0} \end{array} \nonumber \]
Factorización verifica el resultado de que no hay ceros de medio plano derecho para este polinomio, ya que
\[s^4 + 13s^3 + 58 s^2 + 306 s + 260 = (s + 1 + j5)(s + 1 - j5) (s + 1)(s + 10) \nonumber \]
Dos tipos de dificultades pueden ocurrir al aplicar la prueba de Routh. Es posible que el primer elemento en una fila de la matriz sea cero. En este caso, el polinomio original se multiplica por\(s + \alpha\), donde a es cualquier número real positivo, y se repite la prueba. Este procedimiento se ilustra utilizando el polinomio
\[P(s) = s^5 + s^4 + 10s^3 + 10s^2 + 20s + 5 \label{eq4.2.8} \]
El primer elemento de la tercera fila de la matriz es cero.
\[\begin{array} {ccc} {1} & {10} & {20} \\ {1} & {10} & {5} \\ {0} & {15} & {0} \end{array} \nonumber \]
La dificultad se resuelve multiplicando Ecuación\(\ref{eq4.2.8}\) por\(s + 1\), cediendo
\[P'(s) = s^6 + 2s^5 + 11 s^4 + 20 s^3 + 30 s^2 + 25s + 5 \label{eq4.2.10} \]
La matriz para Ecuación\(\ref{eq4.2.10}\) es
\[\begin{array} {cccc} {1} & {11} & {30} & {5} \\ {2} & {20} & {25} & {0} \\ {1} & {17.5} & {5} & {0} \\ {-15} & {15} & {0} & {0} \\ {-18.5} & {5} & {0} & {0} \\ {10.95} & {0} & {0} & {0} \\ {5} & {0} & {0} & {0} \end{array}\label{eq4.2.11} \]
Dado que la multiplicación por\(s + 1\) no sumó ningún ceros de medio plano derecho a la Ecuación\(\ref{eq4.2.8}\), concluimos que los dos ceros de medio plano derecho indicados por la matriz de Ecuación\(\ref{eq4.2.11}\) deben estar contenidos en el polinomio original.
La segunda posibilidad es que una fila entera se convierta en cero. Esta condición indica que hay un par de raíces en el eje imaginario, un par de raíces reales localizadas simétricamente con respecto al origen, o ambos tipos de pares en el polinomio original. Los términos en la fila por encima de la fila de todo cero se utilizan como coeficientes de una ecuación en potencias pares de\(s\) llamada la ecuación auxiliar. Los ceros de esta ecuación son los pares mencionados anteriormente. La ecuación auxiliar se puede diferenciar con respecto a\(s\), y los coeficientes resultantes se utilizan en lugar de la fila todo cero para continuar la matriz. Este tipo de dificultad se ilustra con el polinomio
\[P(s) = s^4 + 11s^3 + 11s^2 + 11s + 10 = (s + j)(s - j) (s + 1) (s + 10)\label{eq4.2.12} \]
La matriz es
\[\begin{array} {ccc} {1} & {11} & {10} \\ {11} & {11} & {0} \\ {10} & {10} & {0} \\ {0} & {0} & {0} \end{array}\label{eq4.2.13} \]
La ecuación auxiliar es
\[Q(s) = 10s^2 + 10\label{eq4.2.14} \]
Las raíces de la ecuación son los dos ceros imaginarios de Ecuación\(\ref{eq4.2.12}\). La ecuación diferenciadora\(\ref{eq4.2.14}\) y el uso del coeficiente distinto de cero para reemplazar el primer elemento de la fila 4 de la ecuación\(\ref{eq4.2.13}\) produce una nueva matriz.
\[\begin{array} {ccc} {1} & {11} & {10} \\ {11} & {11} & {0} \\ {10} & {10} & {0} \\ {20} & {0} & {0} \\ {10} & {0} & {0} \end{array} \nonumber \]
La ausencia de cambios de signo en la matriz verifica que el polinomio original no tenga ceros en el plano de la mitad derecha.
Obsérvese que, si bien no hay polos de bucle cerrado en el plano de la mitad derecha, un sistema con una ecuación característica dada por Ecuación\(\ref{eq4.2.12}\) es inestable por nuestra definición ya que tiene un par de polos en el eje imaginario. Al examinar solo la columna izquierda de la matriz Routh, solo se identifica el número de ceros de medio plano derecho del polinomio probado. Los ceros del eje imaginario se pueden encontrar mediante las manipulaciones que involucran la ecuación auxiliar.
Ayuda de diseño
El criterio de Routh se utiliza con mayor frecuencia para determinar la estabilidad de un sistema de retroalimentación. En ciertos casos, sin embargo, se puede obtener información de diseño más cuantitativa, como se ilustra en los siguientes ejemplos.
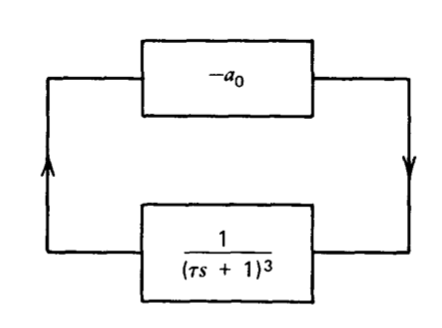
Un oscilador de desplazamiento de fase se puede construir aplicando suficiente retroalimentación negativa alrededor de una red que tiene tres o más polos. Si un amplificador con ganancia independiente de la frecuencia se combina con una red con tres polos coincidentes, el diagrama de bloques para el sistema resultante es como se muestra en la Figura 4.2. El valor de\(a_0\) necesario para sostener oscilaciones puede ser determinado por análisis de Routh. (La prueba de Routh aplicada a este ejemplo ofrece ventajas computacionales en comparación con la factorización directa utilizada para una función de transferencia similar en el ejemplo de la Sección 4.1.)
Las investigaciones de estabilidad para la Figura 4.2 se complican por el hecho de que el
el oscilador no tiene entrada; por lo tanto, no podemos usar los polos de una función de transferencia de entrada a salida para determinar la estabilidad. Debemos señalar que la estabilidad de un sistema lineal es una propiedad del propio sistema y, por lo tanto, es independiente de las señales de entrada que se le puedan aplicar. Cualquier sistema físico inestable demostrará su inestabilidad sin entrada, ya que el comportamiento desbocado será estimulado por el ruido siempre presente. Incluso en un sistema lineal puramente matemático, la estabilidad está determinada por la ubicación de los polos de bucle cerrado, y estas ubicaciones son claramente independientes de entrada.
El análisis del oscilador se inicia recordando que la ecuación característica de cualquier sistema de retroalimentación es uno menos su transmisión en bucle. Por lo tanto
\[P(s) = 1 + \dfrac{a_0}{(\tau s + 1)^3} \nonumber \]
En este y otros cálculos que involucran la ecuación característica, es posible borrar fracciones ya que la ubicación de los ceros no se ve alterada por esta operación. Después de borrar fracciones e identificar coeficientes, la matriz Routh es
\[\begin{array} {cc} {\tau^3} & {3 \tau} \\ {3 \tau^2} & {1 + a_0} \\ {\dfrac{(8 - a_0) \tau}{3}} & {0} \\ {1 + a_0} & {0} \end{array} \nonumber \]
Suponiendo que\(\tau\) es positivo, las raíces con partes reales positivas ocurren para\(a_0 < -1\) (un cero de medio plano derecho) y para\(a_0 > +8\) (dos ceros de medio plano derecho).
El análisis de Laplace indica que la generación de una oscilación sinusoidal de amplitud constante requiere un par de polos en el eje imaginario. En la práctica, un par de polos complejo se ubica ligeramente a la derecha del eje imaginario. Una no linealidad introducida intencionalmente puede entonces ser utilizada para limitar la amplitud de la oscilación (ver Sección 6.3.3). Así, se obtiene un práctico circuito oscilador con\(a_0 > 8\).
La frecuencia de oscilación con se\(a_0 = 8\) puede determinar examinando la matriz con este valor para\(a_0\). Bajo estas condiciones la tercera fila se convierte en todo cero. La ecuación auxiliar es
\[Q(s) = 3\tau^2 s^2 + 9 \nonumber \]
y la ecuación tiene ceros en\(s = \pm j \sqrt{3}/\tau\), indicando oscilación a\(\sqrt{3}/\tau\) radianes por segundo para\(a_0 = 8\).
Como segundo ejemplo del tipo de información de diseño que se puede obtener a través del análisis de Routh, considere un amplificador operacional con una función de transferencia de bucle abierto
\[a(s) = \dfrac{a_0}{(s + 1) (10^{-6} s + 1) (10^{-7} s + 1)} \nonumber \]
Se supone que este amplificador está conectado como un amplificador no inversor de ganancia de unidad, y deseamos determinar el rango de valores de ao para el cual todos los polos de bucle cerrado tienen partes reales más negativas que\(-2 \times 10^5 \text{sec}^{-1}\). Esta condición en la ubicación del polo de bucle cerrado implica que cualquier respuesta de pulso del sistema disminuirá al menos tan rápido como\(K e^{-2 \times 10^5 t}\) después de que el pulso excitante vuelva a cero. La constante depende\(K\) de las condiciones en el momento en que la entrada se convierte en cero.
La ecuación característica para el amplificador es (después de caer términos insignificantes)
\[P(s) = 10^{-13} s^3 + 1.1 \times 10^{-6} s^2 + s + 1 + a_0 \label{eq4.2.20} \]
Para determinar el rango de ao para el cual todos los ceros de esta ecuación característica tienen partes reales más negativas que\(-2 \times 10^5 \text{sec}^{-1}\), sólo es necesario hacer un cambio de variable en Ecuación\(\ref{eq4.2.20}\) y aplicar el criterio de Routh a la ecuación modificada. En particular, la aplicación de la prueba de Routh a un polinomio obtenido sustituyendo
\[\lambda = s + c \nonumber \]
determinará el número de ceros del polinomio original con partes reales más positivas que\(-c\), ya que esta sustitución desplaza las singularidades del\(s\) plano hacia la derecha en una cantidad a\(c\) medida que se mapean en el\(\lambda\) plano. Si la sustitución indicada se realiza con\(c = 2 \times 10^5 \text{sec}^{-1}\), la ecuación\(\ref{eq4.2.20}\) se convierte en
\[P(\lambda) = 10^{-13} \lambda^3 + 10^{-6} \lambda^2 + 0.57 \lambda - 1.57 \times 10^5 + a_0 \nonumber \]
La matriz Routh es
\[\begin{array} {cc} {10^{-13}} & {0.57} \\ {10^{-6}} & {-1.57 \times 10^5 + a_0} \\ {0.59 - 10^{-7} a_0} & {0} \\ {-1.57 \times 10^5 + a_0} & {0} \end{array} \nonumber \]
Esta matriz muestra que Eqn\(\ref{eq4.2.20}\) tiene un cero con una parte real más positiva que\(-2 \times 10^5 \text{sec}^{-1}\) para\(a_0 < 1.57 \times 10^5\), y tiene dos ceros a la derecha de la línea divisoria para\(a_0 > 5.9 \times 10^6\). En consecuencia, todos los ceros tienen partes reales más negativas que\(-2 \times 10^5 \text{sec}^{-1}\) solo para
\[1.57 \times 10^5 < a_0 < 5.9 \times 10^6 \nonumber \]


