6.3: Describiendo la función

La descripción de funciones proporciona un método para el análisis de sistemas no lineales que está estrechamente relacionado con las técnicas de sistemas lineales que involucran gráficos de Bode o fase de ganancia. Es posible utilizar este tipo de análisis para determinar si los ciclos límite (oscilaciones periódicas de amplitud constante) son posibles para un sistema dado. También es posible utilizar funciones descriptivas para predecir la respuesta de ciertos sistemas no lineales a la excitación puramente sinusoidal, aunque este tema no se trata aquí (G. J. Thaler y M. P. Pastel, Analysis and Design of Nonlinear Feedback Control Systems, McGraw-Hill, Nueva York, 1962). Desafortunadamente, dado que la respuesta de frecuencia y la respuesta transitoria de los sistemas no lineales no están directamente relacionadas, la determinación de la respuesta transitoria no es posible a través de la descripción de funciones.

Derivación de la función descriptora

Una función descritora describe el comportamiento de un elemento no lineal para excitación puramente sinusoidal. Así, la señal de entrada aplicada al elemento no lineal para determinar su función de descripción es

\[v_I = E \sin \omega t \nonumber \]

Si la no linealidad no rectifica la entrada (produce una salida d-c) y no introduce subarmónicos, la salida del elemento no lineal se puede expandir en una serie de Fourier de la forma

\[v_O = A_1 (E, \omega ) \cos \omega t + B_1 (E, \omega ) \sin \omega t + A_2 (E, \omega ) \cos 2 \omega t + B_2 (E, \omega ) \sin 2\omega t + \cdots + \nonumber \]

La función de descripción para el elemento no lineal se define como

\[G_D (E, \omega ) = \dfrac{\sqrt{A_1^2 (E, \omega ) + B_1^2 (E, \omega )}}{E} \measuredangle \tan^{-1} \dfrac{A_1 (E, \omega )}{B_1 (E, \omega )}\label{eq6.3.3} \]

La caracterización de funciones descriptivas de un elemento no lineal es paralela a la caracterización de función de transferencia de un elemento lineal. Si se evalúa la función de transferencia de un elemento lineal\(s = j\omega \), la magnitud de la función resultante de una variable compleja es la relación de las amplitudes de las señales de salida y entrada cuando el elemento se excita con una sinusoide a una frecuencia co. De manera similar, el ángulo de la función es el ángulo de fase entre las señales de salida y entrada en condiciones sinusoidales de estado estacionario. Para los elementos lineales estas cantidades deben ser independientes de la amplitud de excitación.

La función descritora indica la amplitud relativa y el ángulo de fase del componente fundamental de la salida de un elemento no lineal cuando el elemento se excita con una sinusoide. En contraste con el caso de los elementos lineales, estas cantidades pueden depender tanto de la amplitud como de la frecuencia de la excitación.

Figura 6.6 Relación para una no linealidad saturante. (\(a\)) Características de transferencia para el elemento saturante. (\(b\)) Formas de onda de entrada y salida para excitación sinusoidal.

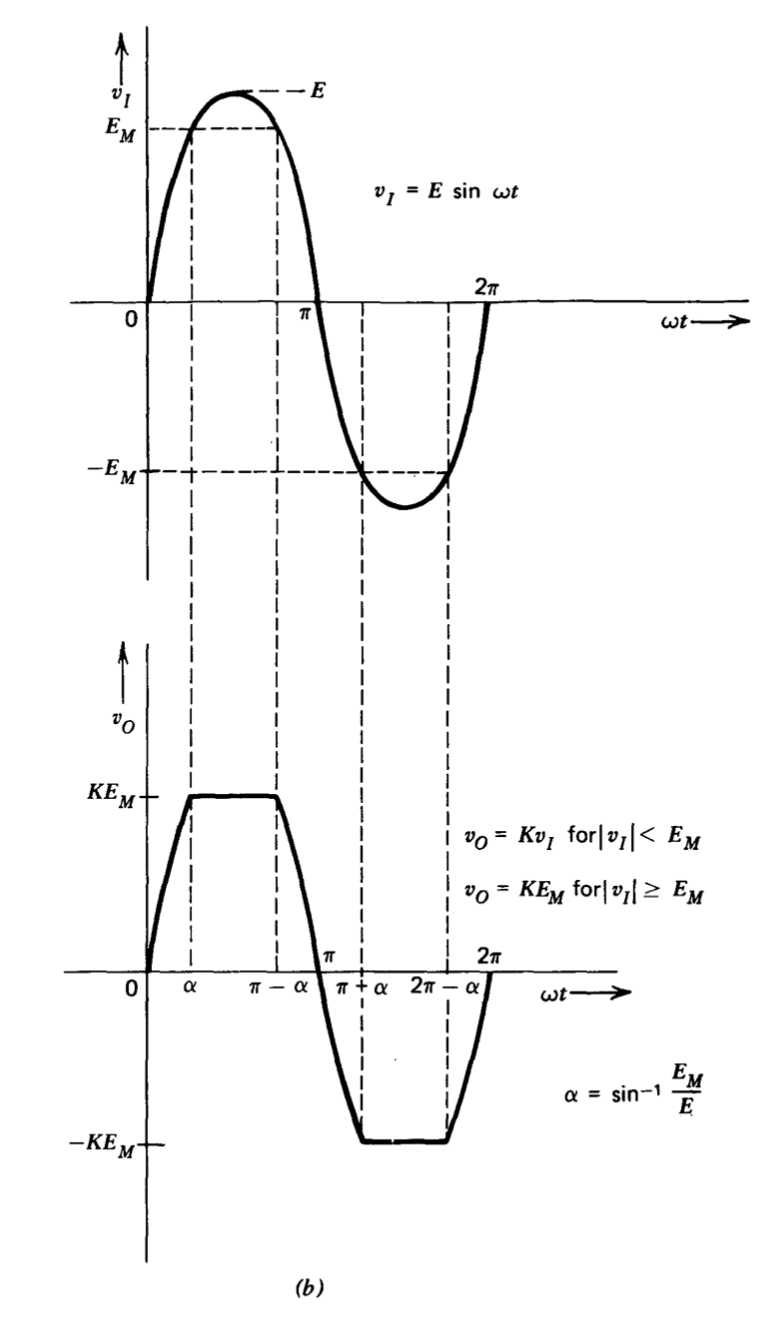
Dos ejemplos ilustran la derivación de la función descritora para elementos no lineales. La Figura 6.6 muestra las características de transferencia de una no linealidad saturante junto con formas de onda de entrada y salida para excitación sinusoidal. Dado que las características de transferencia para este elemento no dependen de la dinámica de la señal de entrada, es claro que la función de descripción debe ser independiente de la frecuencia.

Si la amplitud de entrada\(E\) es menor que\(E_M\),

\[v_O = Kv_1 \nonumber \]

En este caso,

\[G_D = K \measuredangle 0^{\circ} \ \ \ E < E_M \nonumber \]

Para\(E \ge E_M\), la señal de salida en el intervalo\(0 \le \omega t \le \pi\) es

\[v_O = Kv_I \ \ \ \ 0 \le \omega t < \alpha \ \ \ \ \text{ or } \ \ \ \ \pi - \alpha < \omega t \le \pi \nonumber \]

\[v_O = KE_M \ \ \ \ \alpha \le \omega t \le pi - \alpha \nonumber \]

donde

\[\alpha = \sin^{-1} \dfrac{E_M}{E}\nonumber \]

El coeficiente\(A_1\) y\(B_1\) son en este caso,

\[\begin{array} {rcl} {A_1} & = & {\dfrac{2}{\pi} \int_{0}^{\alpha} KE \sin \omega t \cos \omega t \ d \omega t + \dfrac{2}{\pi} \int_{\alpha}^{\pi - \alpha} KE_M \cos \omega t \ d\omega t} \\ {} & \ & {+ \dfrac{2}{\pi} \int_{\pi - \alpha}^{\pi} KE \sin \omega t \cos \omega t \ d \omega t = 0} \end{array} \nonumber \]

\[\begin{array} {rcl} {B_1} & = & {\dfrac{2}{\pi} \int_{0}^{\alpha} KE \sin^2 \omega t \ d \omega t + \dfrac{2}{\pi} \int_{\alpha}^{\pi - \alpha} KE_M \sin \omega t \ d\omega t} \\ {} & \ & {+ \dfrac{2}{\pi} \int_{\pi - \alpha}^{\pi} KE \sin^2 \omega t \ d \omega t = 0} \\ {} & = & {\dfrac{2KE}{\pi} \left [\sin^{-1} \dfrac{E_M}{E} + \dfrac{E_M}{E} \sqrt{1 - \left (\dfrac{E_M}{E} \right )^2} \right ]} \end{array} \nonumber \]

Usando la ecuación\(\ref{eq6.3.3}\), obtenemos

\[G_D (E) = K \measuredangle 0^{\circ} \ \ \ E \le E_M \nonumber \]

\[G_D (E) = \dfrac{2K}{\pi} \left (\sin^{-1} R + R \sqrt{1 - R^2} \right ) \measuredangle 0^{\circ} \ \ \ E > E_M \nonumber \]

donde\(R = E_M/E\).

Figura 6.7 Relaciones para un elemento con histéresis. (\(a\)) Características de transferencia. (\(b\)) Formas de onda de entrada y salida para excitación sinusoidal.

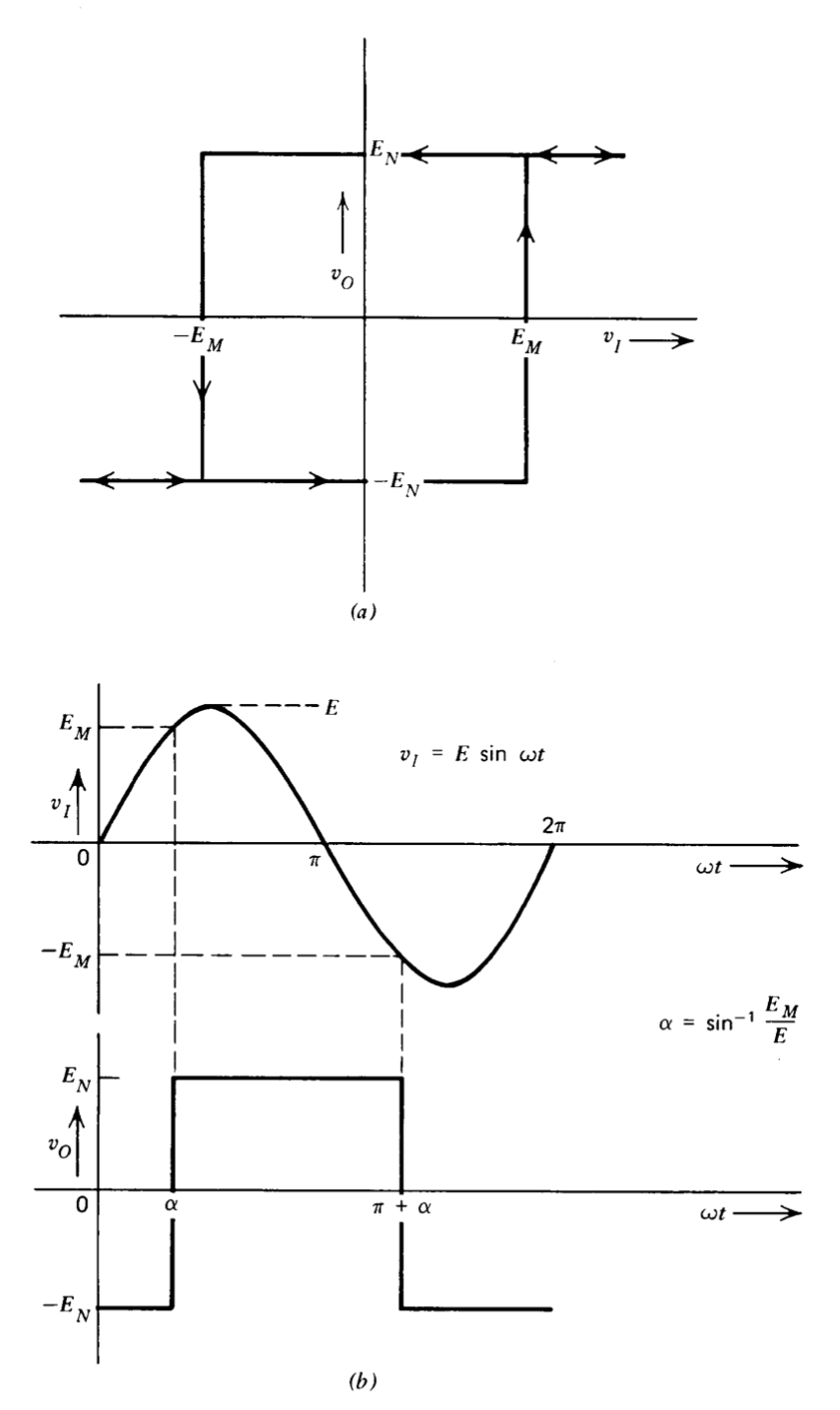
Las características de transferencia de un elemento con histéresis, como un disparador Schmitt o un relé, se muestran en la Figura 6.7\(a\). La memoria asociada a este tipo de elementos produce un desplazamiento de fase entre el componente fundamental de la salida y la sinusoide de entrada aplicada a la misma como se muestra en la Figura 6.7\(b\). Es necesario que la amplitud pico de la señal de entrada supere\(E_M\) para tener la señal de salida distinta a una constante.

Varias características de la señal de salida permiten escribir la función de descripción para este elemento. Entre las relaciones relevantes se incluyen las siguientes.

1. Si bien hay desplazamiento de fase entre la señal de entrada y el componente funda mental de la salida, ni la cantidad de este desplazamiento de fase ni la amplitud de la señal de salida dependen de la frecuencia de excitación.
2. La amplitud del componente fundamental de una onda cuadrada con una amplitud pico\(E_N\) es\(4 E_N/\pi \).
3. El desplazamiento de fase relativo entre la señal de entrada y el componente fundamental de la salida es\(\sin^{-1} (E_M/E)\), con la salida retrasando la entrada.

Tabla 6.1 Descripción de las funciones

Entrada de no linealidad =\(v_I = E \sin \omega t\)	Describiendo la función (Todos son independientes de la frecuencia.)
\ (V_i = E\ sin\ omega t\) ">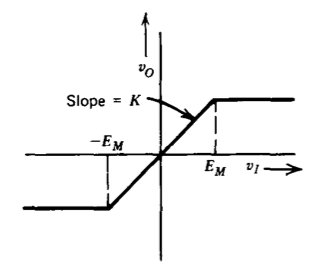	\(G_D (E) = K \measuredangle 0^{\circ} \ \ E \le E_M\) \(G_D (E) = \dfrac{2K}{\pi} \left (\sin^{-1} R + R \sqrt{1 - R^2} \right ) \measuredangle 0^{\circ},\) \(E > E_M\) donde\(R = \dfrac{E_M}{E}\)
\ (V_i = E\ sin\ omega t\) ">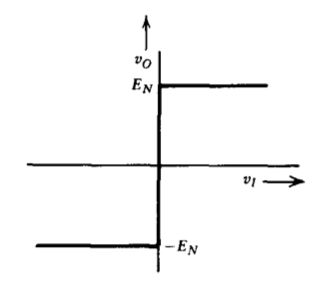	\(G_D (E) = \dfrac{4E_N}{\pi E} \measuredangle 0^{\circ}\)
\ (V_i = E\ sin\ omega t\) ">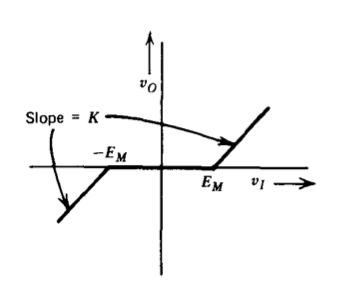	\(G_D (E) = 0 \measuredangle 0^{\circ} \ \ E \le E_M\) \(G_D (E) = K \left [1 - \dfrac{2}{\pi} \left (\sin^{-1} R + R \sqrt{1 - R^2} \right ) \right ] \measuredangle 0^{\circ},\) \(E > E_M\) donde\(R = \dfrac{E_M}{E}\)
\ (V_i = E\ sin\ omega t\) ">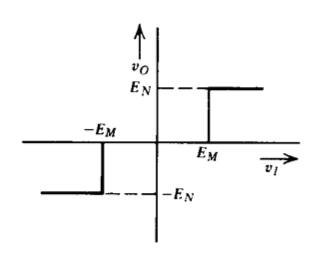	\(G_D (E) = 0 \measuredangle 0^{\circ} \ \ E \le E_M\) \(G_D (E) = \dfrac{4E_N}{\pi E} \sqrt{1 - R^2} \measuredangle 0^{\circ}, \ \ E > E_M\) donde\(R = \dfrac{E_M}{E}\)
\ (V_i = E\ sin\ omega t\) ">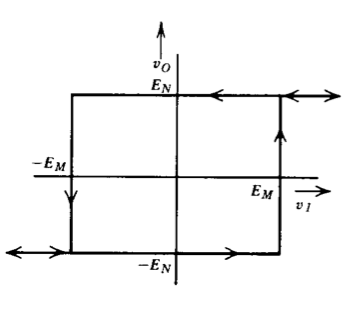	\(E\)debe exceder\(E_M\) o un término d-c resultados. \(G_D (E) = \dfrac{4E_N}{\pi E} \measuredangle -\sin^{-1} R\) donde\(R = \dfrac{E_M}{E}\)

Combinar estas relaciones demuestra que

\[\begin{array} {rcl} {G_D (E)} & = & {\dfrac{4E_N}{\pi E} \measuredangle -\sin^{-1} \dfrac{E_M}{E} \ \ E \ge E_M} \\ {G_D (E)} & \ & {\text{undefined otherwise}} \end{array} \nonumber \]

En la Tabla 6.1 se enumeran las funciones descriptivas para varias no linealidades comunes. Dado que las características de transferencia mostradas son todas independientes de la frecuencia de la señal de entrada, las funciones de descripción correspondientes dependen solo de la amplitud de la señal de entrada. Si bien esta restricción no es necesaria para utilizar técnicas de función descriptora, la complejidad asociada con el análisis de funciones descriptivas de sistemas que incluyen no linealidades dependientes de la frecuencia a menudo limita su utilidad.

Figura 6.8 Saturación suave como combinación de dos no linealidades. (\(a\)) Características de transferencia. (\(b\)) Descomposición en dos no linealidades.

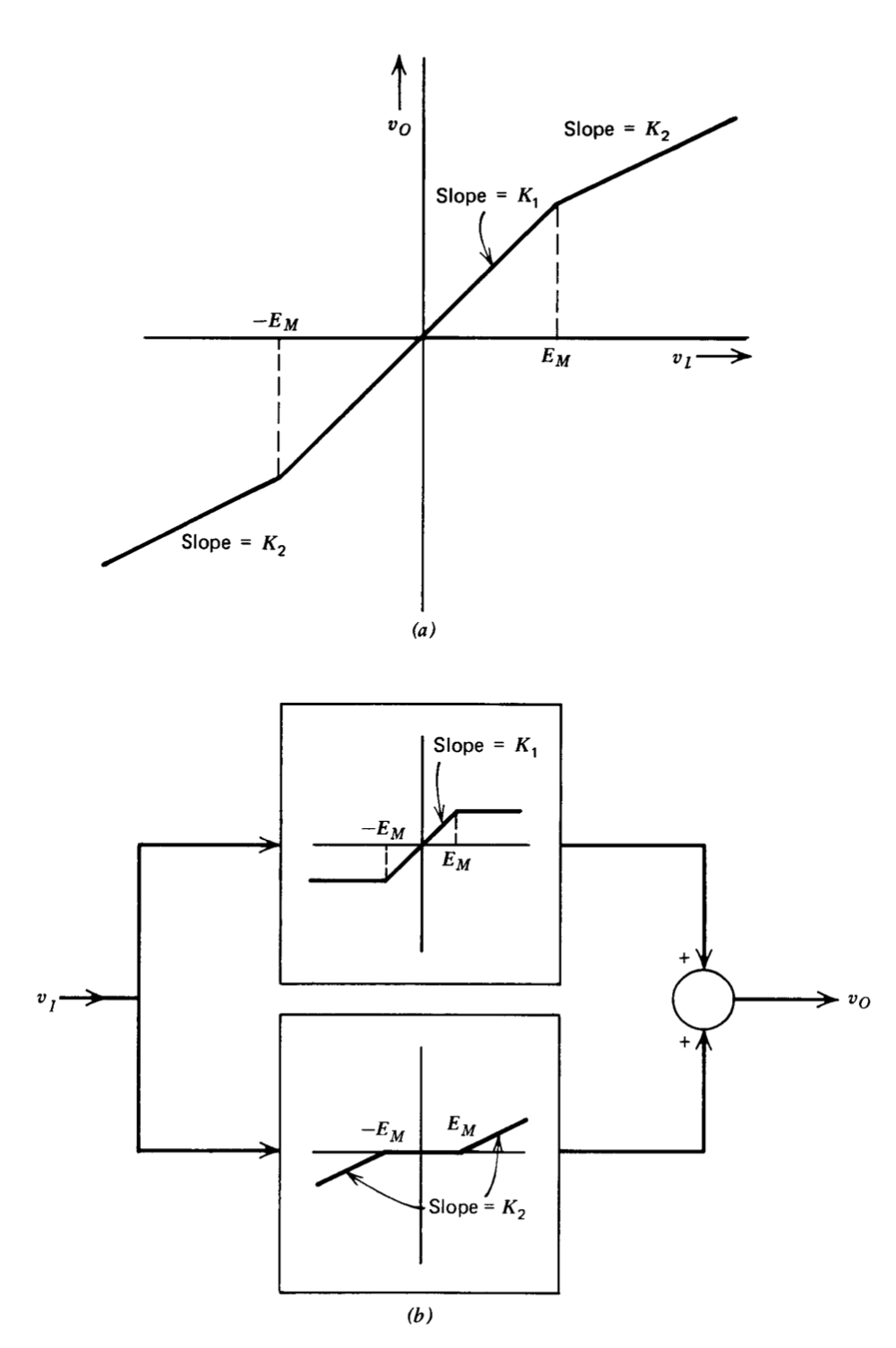
La linealidad de la serie de Fourier puede explotarse para determinar la función descriptora de ciertas no linealidades a partir de las funciones descriptoras conocidas de otros elementos. Consideremos, por ejemplo, las características de saturación suave que se muestran en la Figura 6.8\(a\). Las características de entrada-salida para este elemento se pueden duplicar combinando dos elementos tabulados como se muestra en la Figura 6.8\(b\). Dado que el componente fundamental de la salida del sistema de la Figura 6.8\(b\) es la suma de los componentes fundamentales de las dos no linealidades

\[G_D(E) = K_1 \measuredangle 0^{\circ} E \le E_M \nonumber \]

\[\begin{array} {rcl} {G_D (E)} & = & {\left [ \dfrac{2K_1}{\pi} \left (\sin^{-1} R + R \sqrt{1 - R^2} \right ) + K_2 - \dfrac{2K_2}{\pi} \left ( \sin^{-1} R + R \sqrt{1 - R^2} \right ) \right ] \measuredangle 0^{\circ}} \\ {} & = & {\left [ K_2 + \dfrac{2(K_1 - K_2)}{\pi} \left ( \sin^{-1} R + R \sqrt{1 - R^2} \right ) \right ] \measuredangle 0^{\circ}} \end{array} \nonumber \]

para\(E > E_M\), donde\(R = \sin^{-1} (E_M/ E)\).

Análisis de Estabilidad con la Ayuda de Describir Funciones

Las funciones descriptivas se utilizan con mayor frecuencia para determinar si los ciclos límite (oscilaciones periódicas de amplitud estable) son posibles para un sistema dado, y para determinar las amplitudes de varias señales cuando estas oscilaciones están presentes.

Figura 6.9 Sistema dispuesto para el análisis de la función de descripción.

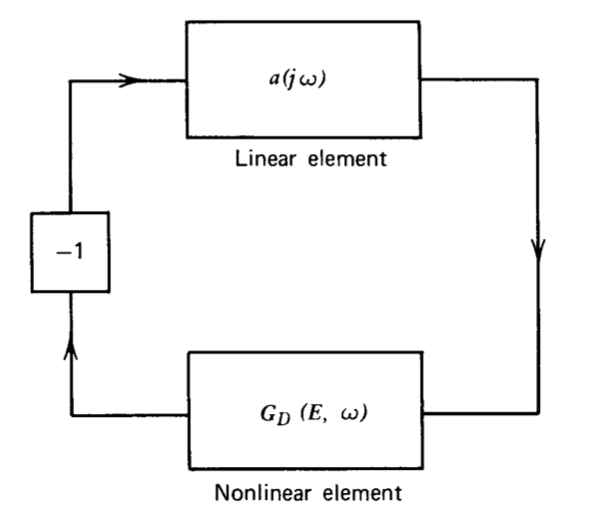
El análisis de la función descriptora se simplifica si el sistema puede disponerse en una forma similar a la que se muestra en la Figura 6.9. El bloque inversor se incluye para representar la inversión convencionalmente indicada en el punto de suma en un sistema de retroalimentación negativa. Dado que la intención del análisis es examinar la posibilidad de oscilaciones en estado estacionario, los puntos de entrada y salida del sistema son irreveladores. La característica importante de la topología mostrada en la Figura 6.9 es que un solo elemento no lineal aparece en un bucle con un solo elemento lineal. Por supuesto, el elemento lineal mostrado puede representar la reducción de una interconexión compleja de elementos lineales en el sistema original a una sola función de transferencia. Las técnicas descritas en las Secciones 2.4.2 y 2.4.3 suelen ser útiles para estas reducciones.

Figura 6.10 Sistema no lineal. (\(a\)) Circuito. (\(b\)) Características del Zener-limitador.

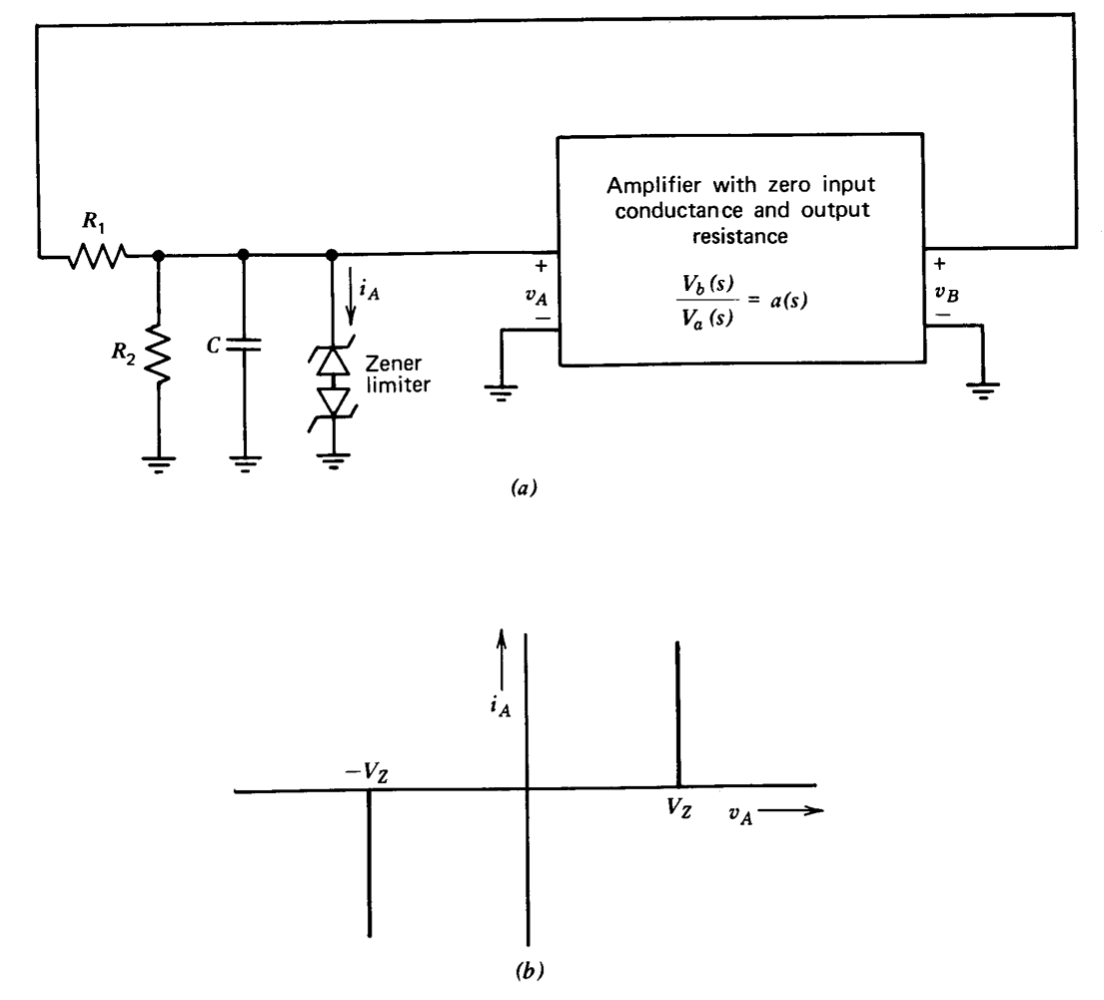
El sistema mostrado en la Figura 6.10 ilustra un tipo de manipulación que simplifica el uso de funciones descriptivas en ciertos casos. Un limitador que consiste en diodos Zener adosados se incluye en un circuito que también contiene un amplificador y una red de resistencia-condensador. Se supone que el limitador Zener tiene las características lineales a trozos que se muestran en la Figura 6.10\(b\).

La función de descripción para la red no lineal que incluye\(R_1, R_2, C\), y el limitador podría calcularse asumiendo una señal sinusoidal para\(v_B\) y encontrando la amplitud y el ángulo de fase relativo del componente fundamental de\(v_A\). La función de descripción resultante sería dependiente de la frecuencia. Se obtiene una representación más satisfactoria si el valor de la corriente Zener\(i_A\) se determina en función de la tensión aplicada a la red.

\[i_A = \dfrac{v_B}{R_1} - \dfrac{v_A}{R_1 ||R_2} - C \dfrac{dv_A}{dt}\label{eq6.3.15} \]

El limitador Zener fuerza las restricciones adicionales

\[v_A = + V_Z \ \ \ i_A > 0\label{eq6.3.16} \]

\[v_A = - V_Z \ \ \ i_A < 0\label{eq6.3.17} \]

Figura 6.11 Sistema de modelado de la Figura 6.10 como un solo bucle. (\(a\)) Representación de diagrama de bloques de red no lineal. (\(b\)) Representación en diagrama de bloques del sistema completo. (\(c\)) Reducida a la forma de la Figura 6.9.

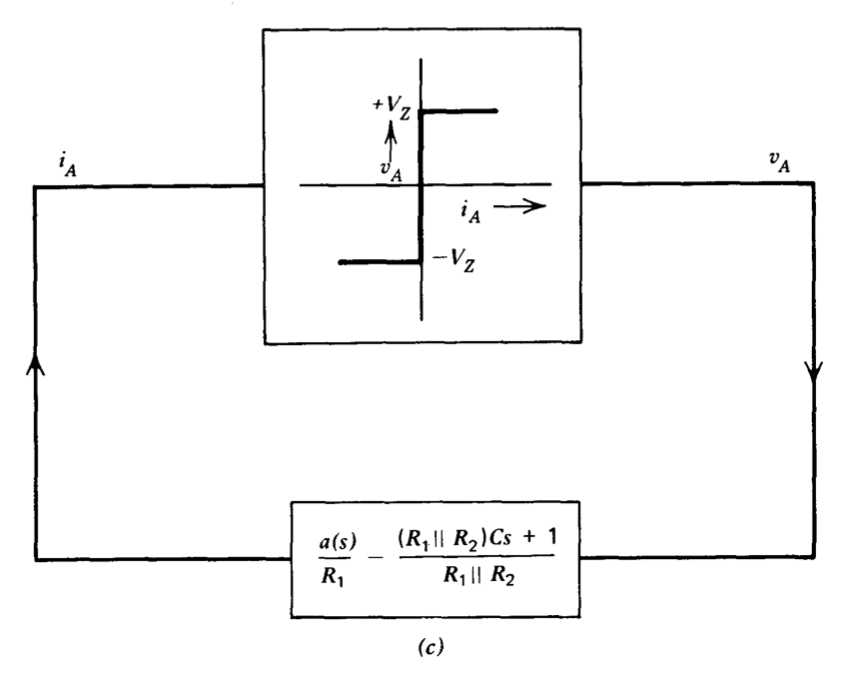
Ecuaciones\(\ref{eq6.3.15}\),\(\ref{eq6.3.16}\) e\(\ref{eq6.3.17}\) implican que el diagrama de bloques mostrado en la Figura 6.11\(a\) puede ser utilizado para relacionar las variables en la red no lineal. La característica agradable de esta representación es que la no linealidad restante se puede caracterizar por una función de descripción independiente de la frecuencia. La Figura 6.11\(b\) ilustra el diagrama de bloques que resulta cuando la red se combina con el amplificador. Las dos trayectorias lineales en este diagrama se combinan en la Figura 6.1\(c\), que es la forma sugerida para el análisis.

Una vez que un sistema ha sido reducido a la forma mostrada en la Figura 6.9, se puede analizar mediante la descripción de funciones. La aproximación de la función de descripción establece que las oscilaciones pueden ser posibles si existen valores particulares de\(E_1\) y\(\omega_1\) existen de tal manera que

\[a(j\omega_1) G_D (E_1, \omega_1) = -1\label{eq6.3.18} \]

o

\[a(j\omega_1) = \dfrac{-1}{G_D(E_1, \omega_1)}\label{eq6.3.19} \]

La satisfacción de Ecuación\(\ref{eq6.3.18}\) y\(\ref{eq6.3.19}\) no garantiza que el sistema en cuestión oscilará. Es posible que un sistema que satisfaga la Ecuación\(\ref{eq6.3.18}\) y\(\ref{eq6.3.19}\) sea estable para un rango de niveles de señal y deba activarse en oscilación, por ejemplo, superando un nivel de señal particular en la entrada al elemento no lineal. Una segunda posibilidad es que la igualdad de Ecuación\(\ref{eq6.3.18}\) y\(\ref{eq6.3.19}\) no describa una oscilación de amplitud estable. En este caso, si se supone que el sistema está oscilando con valores de parámetros dados en Ecuación\(\ref{eq6.3.18}\) y\(\ref{eq6.3.19}\), una pequeña perturbación de amplitud es divergente y conduce a una amplitud creciente o decreciente. Como veremos, se puede utilizar el método para resolver estas cuestiones. El análisis de función descriptora también predice que si existen oscilaciones de amplitud estable, la frecuencia de las oscilaciones será\(\omega_1\) y la amplitud del componente fundamental de la señal aplicada a la no linealidad será\(E_1\).

La discusión anterior muestra cuán cerca el análisis de estabilidad de la función descriptora de sistemas no lineales es paralelo al análisis Nyquist o Bode-plot de sistemas lineales. En particular, las oscilaciones se predicen para sistemas lineales a frecuencias donde la transmisión de bucle es +1, mientras que el análisis de la función de descripción indica posibles oscilaciones para combinaciones de amplitud-frecuencia que producen el equivalente de sistema no lineal de transmisión de bucle unitario.

La aproximación básica del análisis de la función descriptora es ahora evidente. Se supone que bajo condiciones de oscilación en estado estacionario, la entrada al elemento no lineal consiste en una sinusoide de frecuencia única. Si bien esta suposición ciertamente no se satisface exactamente porque el elemento no lineal genera armónicos que se propagan alrededor del bucle, a menudo es una aproximación útil por dos razones. Primero, muchas no linealidades generan armónicos con amplitudes que son pequeñas en comparación con lo fundamental. En segundo lugar, dado que muchos elementos lineales en los sistemas de retroalimentación son de naturaleza de paso bajo, los armónicos en la señal devuelta al elemento no lineal a menudo son atenuados en mayor grado que el fundamental por los elementos lineales. La segunda razón indica una mejor aproximación para los sistemas de paso bajo de orden superior.

La existencia de la relación indicada en la Ecuación\(\ref{eq6.3.18}\) y a menudo\(\ref{eq6.3.19}\) es disuadida gráficamente. La función de transferencia del elemento lineal se representa en forma de fase de ganancia. La función también\(- 1/G_D(E, \omega )\) se traza en la misma gráfica. Si\(G_D\) es independiente de la frecuencia,\(- 1/G_D(E)\) es una sola curva con\(E\) un parámetro a lo largo de la curva. La condición necesaria para la oscilación se satisface si existe una intersección de las dos curvas. La frecuencia se puede determinar a partir de la\(a(j\omega )\) curva, mientras que la amplitud del componente fundamental de la señal hacia la no linealidad se determina a partir de la\(- 1/G_D(E)\) curva. Si la no linealidad depende de la frecuencia, se traza una familia de curvas\(- 1/G_D(E, \omega_1), -1/G_D(E, \omega_2)\),...,. La condición de oscilación se satisface si la\(-1/G_D(E, \omega_i)\) curva se cruza con la\(a(j\omega )\) curva en el punto\(a(j\omega_i)\).

La satisfacción de Ecuación\(\ref{eq6.3.18}\) y\(\ref{eq6.3.19}\) es una condición necesaria aunque no suficiente para que exista un ciclo límite. También es necesario asegurar que la oscilación predicha por la intersección sea estable en amplitud. Para probar la estabilidad de amplitud, se supone que la amplitud\(E\) aumenta ligeramente, y el punto correspondiente al valor perturbado de\(E\) se encuentra en la\(- 1/G_D (E, \omega)\) curva. Si este punto se encuentra a la izquierda de la\(a(j\omega )\) curva, la geometría implica que los polos del sistema (El concepto de polo es estrictamente válido solo para un sistema lineal. Una vez que aplicamos la aproximación de la función de descripción (que es un tipo particular de linealización sobre un punto operativo definido por una amplitud de señal), tomamos la misma libertad con la definición de polo que con los sistemas que han sido linealizados por otros métodos.) se encuentran en el plano de la mitad izquierda para un mayor valor de\(E\), tendiendo a restaurar la amplitud a su valor original. Alternativamente, si el punto perturbado se encuentra a la derecha de la\(a(j\omega )\) curva, una oscilación de amplitud creciente resulta de la perturbación y no es posible un ciclo límite con parámetros predichos por la intersección. Estas relaciones se pueden verificar aplicando la prueba de estabilidad Nyquist a la transmisión en bucle, que incluye la función de transferencia lineal y la función descritora de interés.

Cabe señalar que la estabilidad de sistemas no lineales arbitrariamente complejos que combinan una multiplicidad de elementos no lineales en un bucle con elementos lineales puede, al menos en teoría, determinarse mediante funciones descriptivas. Por ejemplo, se podrían construir numerosas gráficas Nyquist correspondientes a las transmisiones de bucle no lineal para una variedad de amplitudes de señal para determinar si existe la posibilidad de inestabilidad. Desafortunadamente, el esfuerzo requerido para completar este tipo de análisis es generalmente prohibitivo.

Ejemplos

Dado que el análisis de la función de descripción predice la existencia de ciclos de límite de amplitud estable, es particularmente útil para la investigación de osciladores, y por esta razón los dos ejemplos de esta sección involucran circuitos osciladores.

La discusión de la Sección 4.2.2 mostró que es posible producir oscilaciones sinusoidales aplicando retroalimentación negativa alrededor de una red de desplazamiento de fase con tres polos de eje real ubicados de manera idéntica. Si la magnitud de la transmisión en bucle de baja frecuencia es exactamente 8, los polos de bucle cerrado del sistema están en el eje imaginario y, por lo tanto, las oscilaciones resultantes son estables en amplitud. Es posible controlar la magnitud de la transmisión de bucle precisamente por medio de un bucle de retroalimentación auxiliar que mide la amplitud de la oscilación y ajusta la transmisión de bucle para regular esta amplitud. Esta aproximación al control de amplitud se discute en la Sección 12.1.4.

Figura 6.12 Oscilador de desplazamiento de fase con limitación.

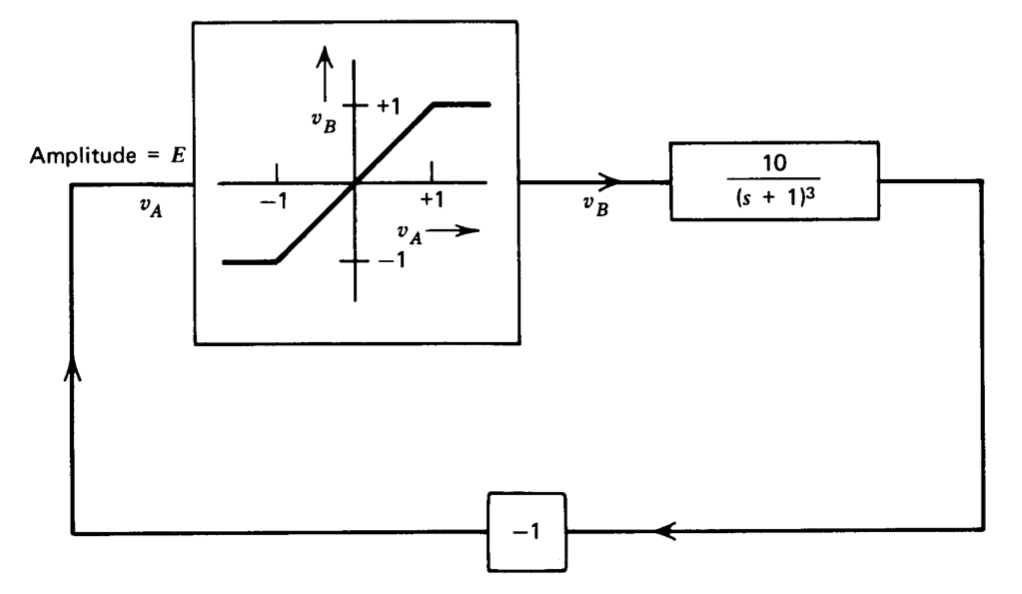
En la Figura 6.12 se ilustra un enfoque alternativo y más sencillo que a menudo se utiliza. La transmisión en bucle del sistema para niveles de señal pequeños se hace lo suficientemente grande (en este caso 10) para asegurar oscilaciones de amplitud creciente si los niveles de señal son tales que el limitador permanece lineal. A medida que la amplitud máxima de la señal VA aumenta más allá de uno, el limitador reduce la magnitud de la transmisión de bucle (en un sentido de función de descripción) para estabilizar la amplitud de las oscilaciones.

La función descriptora para el limitador en la Figura 6.12 es (ver Tabla 6.1)

\[G_D (E) = 1 \measuredangle 0^{\circ} \ \ \ E \le 1\label{eq6.3.20} \]

\[G_D (E) = \dfrac{2}{\pi} \left (\sin^{-1} \dfrac{1}{E} + \dfrac{1}{E} \sqrt{1 - \dfrac{1}{E^2}} \right ) \measuredangle 0^{\circ} \ \ \ E > 1\label{eq6.3.21} \]

Figura 6.13 Análisis descriptivo de la función del oscilador de desplazamiento de fase.

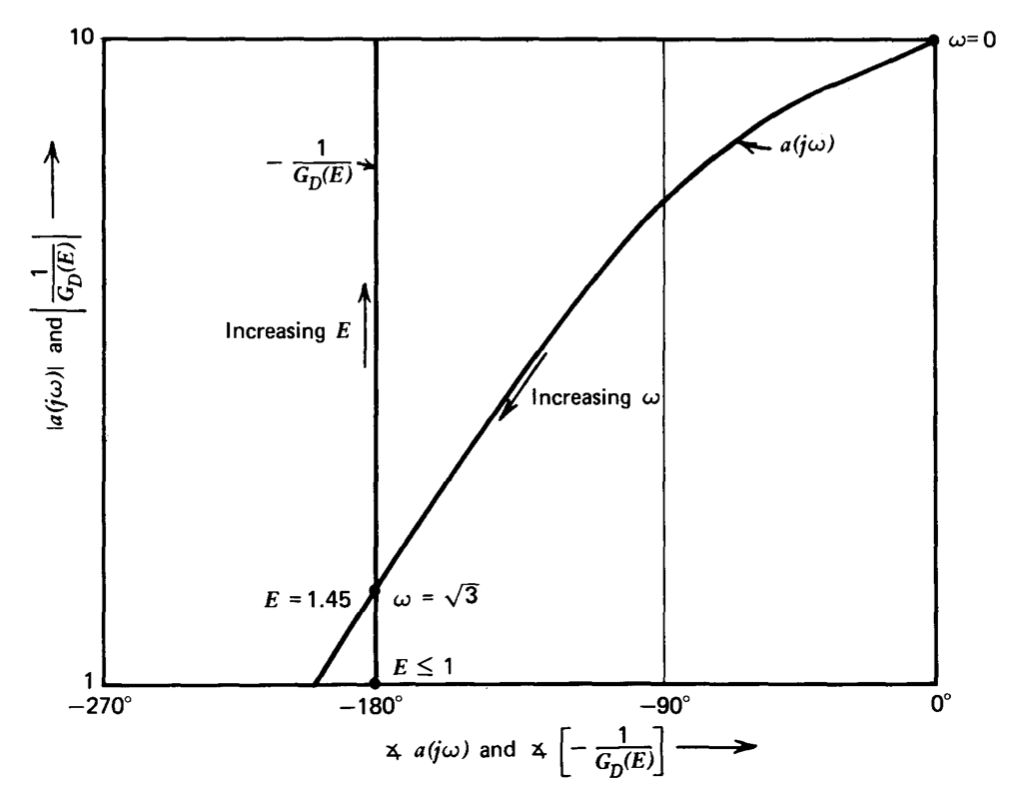
Esta función disminuye monótonamente a medida que\(E\) aumenta más allá de uno. Así la cantidad\(-1/G_D(E)\) aumenta monótonamente por\(E\) más de uno y tiene un ángulo de\(-180^{\circ}\). El comportamiento general\(-1/G_D(E)\) y la función de transferencia de la porción lineal del circuito oscilador se esbozan en el plano de fase de ganancia de la Figura 6.13.

Se observa que la intersección que se muestra representa una oscilación de amplitud estable cuando se utiliza la prueba propuesta en la última sección. Un incremento en\(E\)

del valor en la intersección mueve el\(-1/G_D(E)\) punto a la izquierda de la\(a(j\omega)\) curva. El significado físico de la regla es el siguiente. Supongamos que el sistema está oscilando con el valor de\(E\) necesario hacer\(G_D(E) a(j \sqrt{3}) = -1\). Un incremento incremental en el valor de\(E\) disminuye la magnitud de\(G_D(E)\) y por lo tanto disminuye la transmisión en bucle por debajo del valor necesario para mantener una oscilación de amplitud constante. La amplitud disminuye hasta que\(E\) se restablece su valor original. De manera similar, una disminución incremental en\(E\) conduce a una oscilación de amplitud creciente hasta\(E\) alcanzar su valor de equilibrio.

La magnitud de\(E\) bajo condiciones de estado estacionario se puede determinar directamente a partir de la Ecuación\(\ref{eq6.3.20}\) y\(\ref{eq6.3.21}\). La magnitud de\(a(j\omega)\) a la frecuencia donde su desplazamiento de fase if\(-180^{\circ}\), (\(\omega = \sqrt{3}\)), es 1.25. Así ocurren oscilaciones con\(G_D(E) = 0.8\). Resolviendo Ecuación\(\ref{eq6.3.20}\) y\(\ref{eq6.3.21}\) para el valor requerido de\(E\) por prueba y error resulta en\(E \simeq 1.45\), y este valor corresponde a la amplitud del componente fundamental de\(v_A\).

La validez de la suposición de función descriptora respecto a la pureza de la señal en la entrada del elemento no lineal se demuestra fácilmente para este ejemplo. Si se aplica una sinusoide al limitador, solo los armónicos impares están presentes en su señal de salida, y las amplitudes de los armónicos superiores disminuyen monótonamente. Los cálculos habituales de la serie Fourier muestran que

la relación de la magnitud del tercer armónico a la de la fundamental en la salida del limitador es de 0.14 para una sinusoide de amplitud de pico de 1,45 voltios como entrada del limitador. Los elementos lineales atenúan el tercer armónico de una sinusoide\(\sqrt{3}\) radián por segundo en un factor de 18 mayor que el fundamental. Así, la relación de tercer armónico a fundamental es aproximadamente 0.008 en la entrada al elemento no lineal. Las amplitudes de los armónicos superiores son insignificantes ya que sus magnitudes en la salida del limitador son menores y ya que son atenuadas en mayor medida por el elemento lineal. Como cuestión de interés práctico, la atenuación proporcionada por la red de desplazamiento de fase a armónicos es la razón por la que las buenas prácticas de diseño dictan el uso de la señal fuera de la red de desplazamiento de fase en lugar de la del limitador como señal de salida del oscilador.

Figura 6.14 Generador de funciones. (\(a\)) Configuración. (\(b\)) Formas de onda.

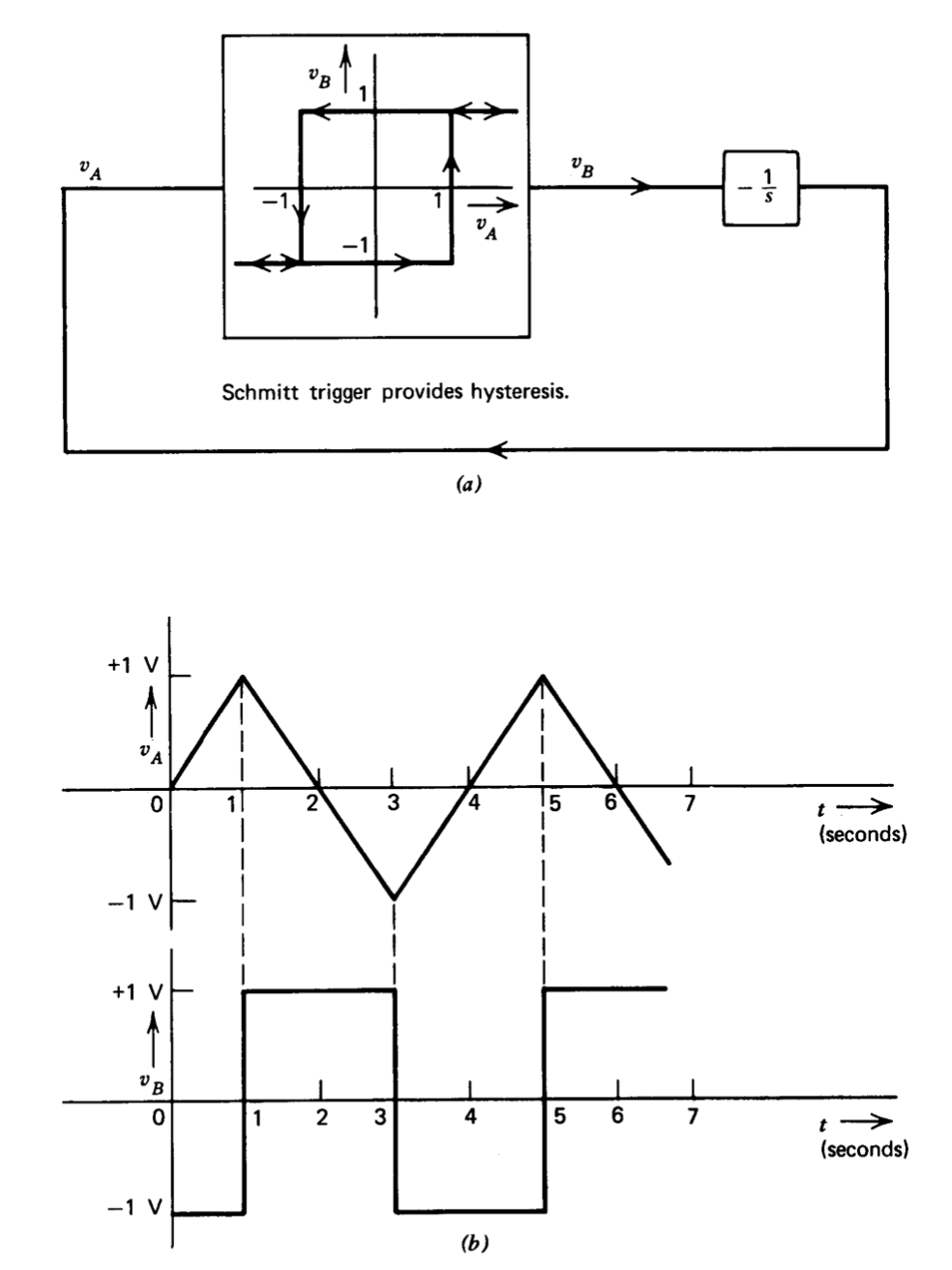
La Figura 6.14\(a\) muestra otra configuración de oscilador que se utiliza como segundo ejemplo de análisis de función de descripción. Este circuito, que combina un disparador Schmitt y un integrador, es una representación simplificada del utilizado en varios generadores de funciones disponibles comercialmente. Se puede demostrar mediante evaluación directa que la señal en la entrada al elemento no lineal es una onda triangular pico a pico de dos voltios con un período de cuatro segundos y que la señal en la salida del elemento no lineal es una onda cuadrada de pico a pico de dos voltios a la misma frecuencia. Los cruces por cero de estas dos señales se desplazan en un segundo como se muestra en la Figura 6.14\(b\). La relación del tercer armónico a lo fundamental en la entrada al elemento no lineal es 1/9, un valor considerablemente mayor que en el ejemplo anterior.

La Tabla 6.1 muestra que la función descritora para esta no linealidad es

\[G_D (E) = \dfrac{4}{\pi E} \measuredangle -\sin^{-1} \dfrac{1}{E} \ \ E \ge 1 \nonumber \]

Figura 6.15 Describiendo el análisis de función del generador de funciones.

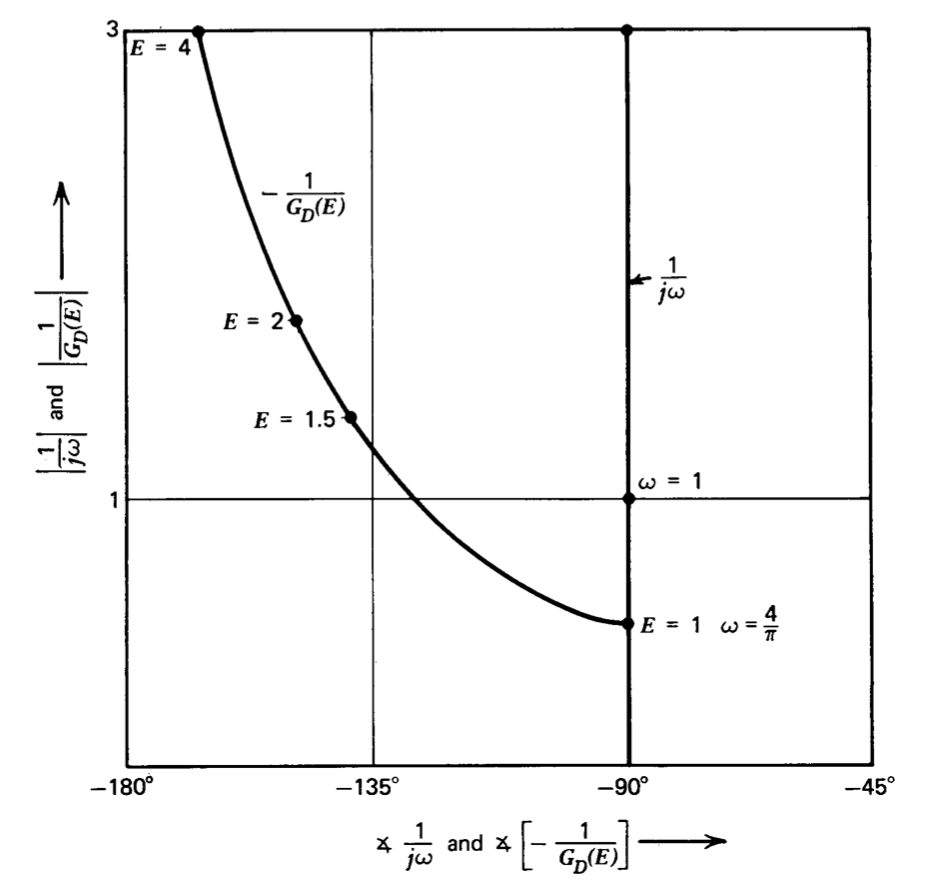
La cantidad\(-1/G_D(E)\) y la función de transferencia para el elemento lineal se representan en forma de fase de ganancia en la Figura 6.15. La intersección se produce para un valor de\(E\) que da como resultado el retardo de fase máximo\(90^{\circ}\) del elemento no lineal. Los parámetros predichos para el ciclo límite de amplitud estable que implica esta intersección son una amplitud pico a pico para vA de dos voltios y un período de oscilación de aproximadamente cinco segundos. La correspondencia entre estos parámetros y los de la solución exacta es excelente considerando la naturaleza real de las señales involucradas.

Estabilidad Condicional

Figura 6.16 Sistema condicionalmente estable.

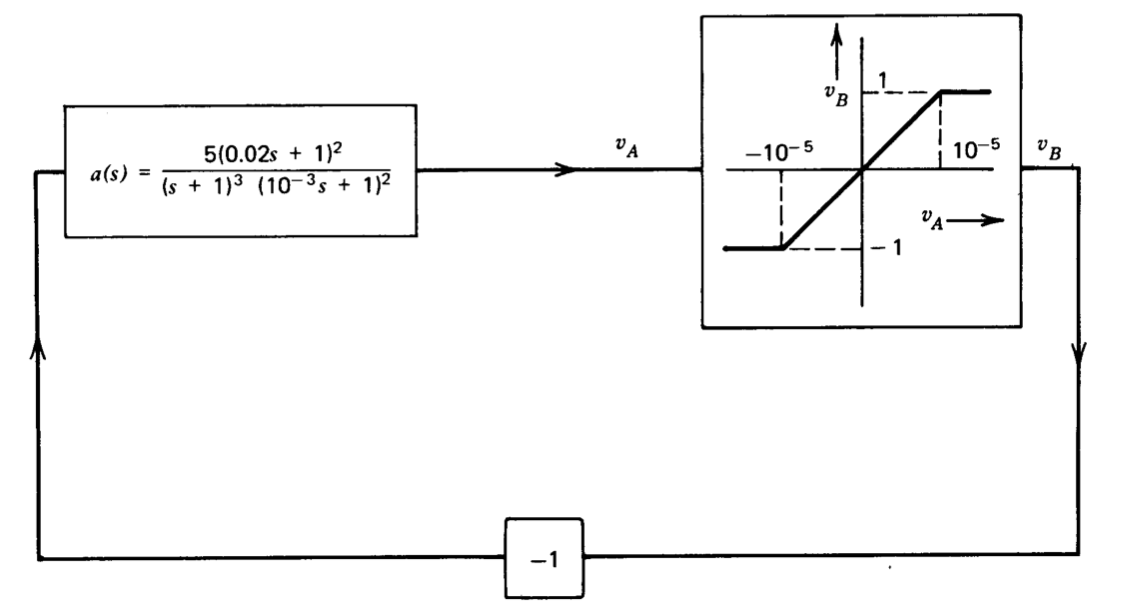
El sistema mostrado en forma de diagrama de bloques en la Figura 6.16 combina una no linealidad saturante con elementos lineales. El negativo de la transmisión de bucle para este sistema, suponiendo que la amplitud de la señal a\(v_A\) es menor que\(10^{-5}\) voltios de manera que la no linealidad proporciona una ganancia de\(10^5\), se determina rompiendo el bucle en el bloque inversor, produciendo

\[-L(s) = 10^5 a(s) = \dfrac{5 \times 10^5 (0.02s + 1)^2}{(s + 1)^3 (10^{-3} s + 1)^2}\label{eq6.3.23} \]

En la Figura 6.17 se muestra un diagrama Nyquist para esta función. La gráfica revela un margen de fase\(40^{\circ}\) combinado con un margen de ganancia de 10, lo que implica un rendimiento moderadamente bien amortiguado. La gráfica también muestra que si la magnitud de la transmisión en bucle de baja frecuencia se reduce en un factor de entre 8 y\(6 \times 10^4\), el sistema se vuelve inestable. Los sistemas que tienen la propiedad de que una disminución en la magnitud de la transmisión de bucle de baja frecuencia desde su valor de centro de diseño los convierte de rendimiento estable a inestable se denominan sistemas condicionalmente estables.

La no linealidad puede producir la disminución de ganancia que resulta en inestabilidad. El sistema mostrado en la Figura 6.16 es estable para valores suficientemente pequeños de la señal\(v_A\). Si la amplitud de\(v_A\) se vuelve lo suficientemente grande, posiblemente por una entrada aplicada externamente (no mostrada en el diagrama) o por el transitorio que puede acompañar al encendido, el sistema puede comenzar a oscilar porque la ganancia de la función de descripción disminuye.

La característica común de los sistemas condicionalmente estables es una curva de fase que cae\(-180^{\circ}\) por debajo de algún rango de frecuencias y luego se recupera para que exista un margen de fase positivo en el cruce. Estas características de fase pueden resultar cuando la amplitud cae\(1/\omega^2\) más rápidamente que en un rango de frecuencias por debajo del cruce. El rolloff de orden superior se utiliza en algunos sistemas ya que combina grandes transmisiones de bucle a frecuencias moderadas con una frecuencia de cruce limitada. Por ejemplo, la función de transferencia

\[-L'(s) = \dfrac{5 \times 10^5}{(2.5 \times 10^3 s + 1)(10^{-3} s + 1)^2}\label{eq6.3.24} \]

tiene la misma ganancia de baja frecuencia y frecuencia de ganancia unitaria que la Ecuación\(\ref{eq6.3.23}\). Sin embargo, la desensitividad asociada a la Ecuación\(\ref{eq6.3.23}\) excede la de\(\ref{eq6.3.24}\) a frecuencias entre\(4 \times 10^4\) radianes por segundo y 50 radianes por segundo debido al rolloff de alto orden asociado con la Ecuación\(\ref{eq6.3.23}\). La ventaja de ganancia alcanza un máximo de aproximadamente 10 a un radián por segundo. Esta mayor ganancia da como resultado una desensitividad significativamente mayor para la transmisión en bucle de la Ecuación en un\(\ref{eq6.3.23}\) amplio rango de frecuencias.

La información cuantitativa sobre el desempeño del sistema que se muestra en la Figura 6.16 se puede obtener mediante análisis de función descriptora. La función de descripción para la no linealidad para\(E > 10^{-5}\) es

\[G_D (E) = \dfrac{2 \times 10^5}{\pi} \left (\sin^{-1} \dfrac{10^{-5}}{E} + \dfrac{10^{-5}}{E} \sqrt{1 - \dfrac{10^{-10}}{E^2}} \right ) \measuredangle 0^{\circ} \nonumber \]

Figura 6.17 Diagrama Nyquist de sistema condicionalmente estable.

Figura 6.18 Describiendo el análisis de función del sistema condicionalmente estable.

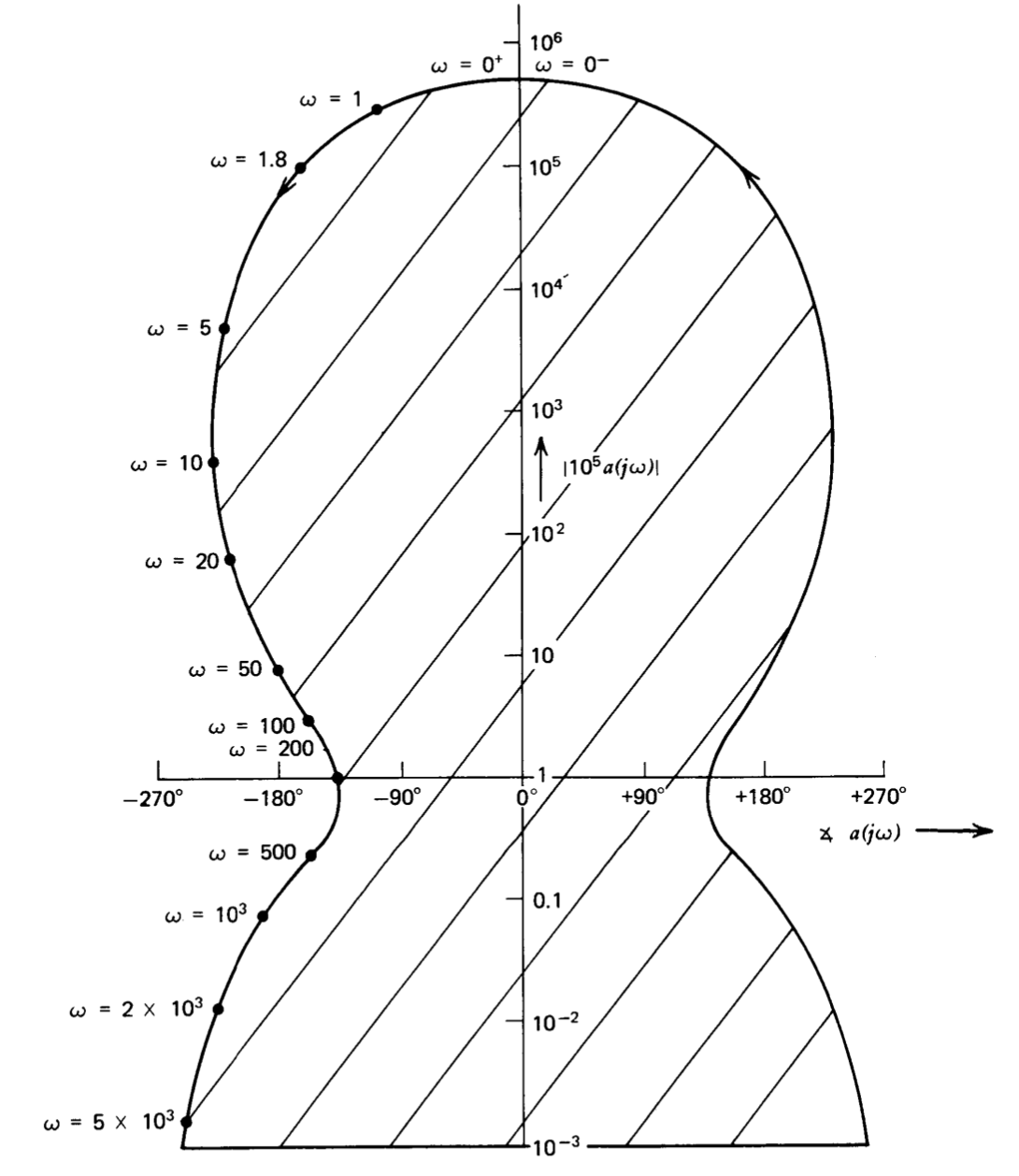
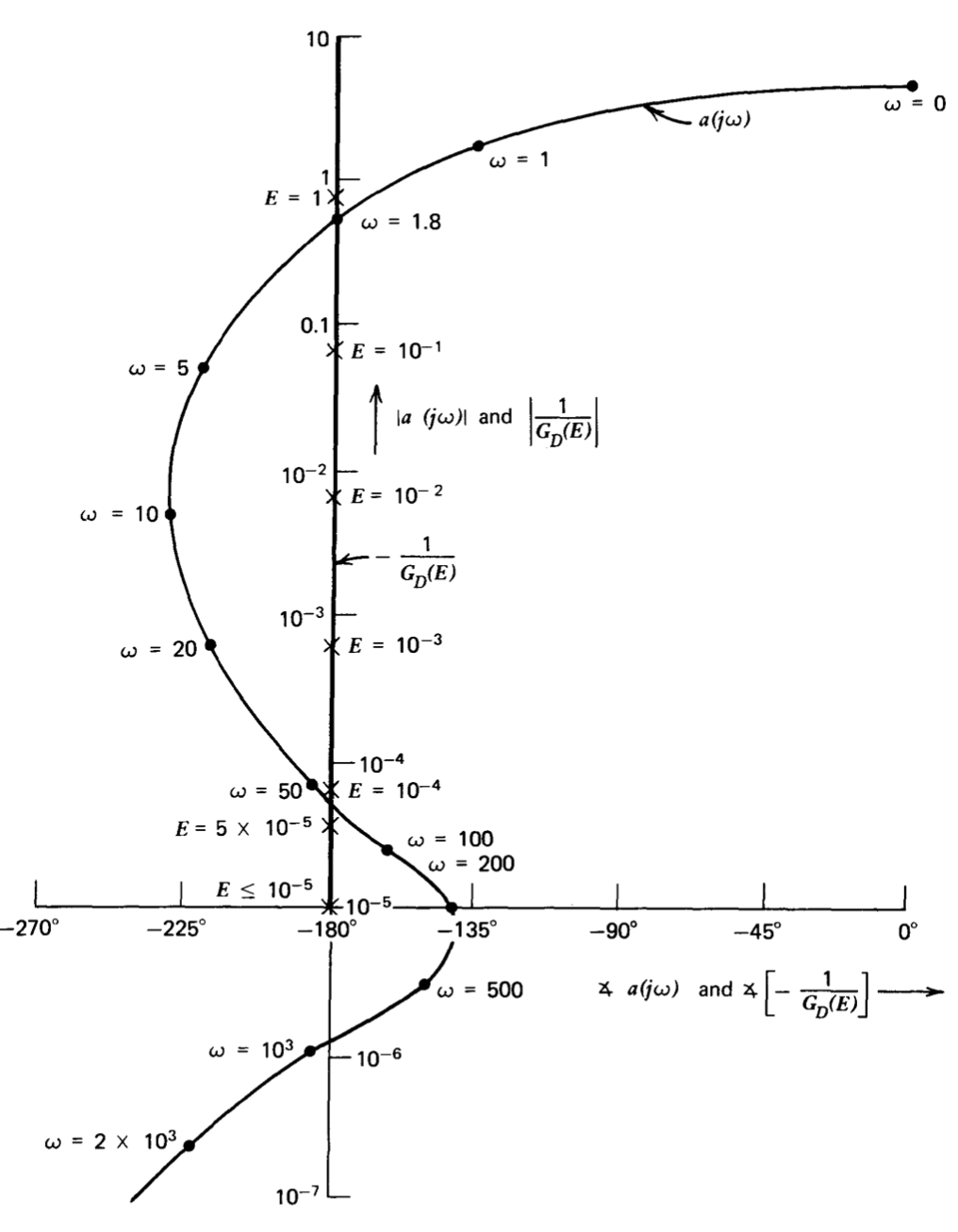
donde\(E\) es la amplitud de la señal (asumida sinusoidal)\(v_A\). Las cantidades\(-1/G_D(E)\) y\(a(j\omega)\) se representan en forma de fase de ganancia en la Figura 6.18, y dos intersecciones son evidentes. La intersección a\(\omega \simeq 50\) radianes por segundo,\(E \simeq 10^{-4}\) voltios no representa un ciclo límite estable. Si se supone que el sistema oscila con estos parámetros, una disminución incremental en la amplitud de la señal\(v_A\) conduce a una disminución adicional de la amplitud y el sistema vuelve a un funcionamiento estable. Este resultado se desprende de la regla mencionada en la Sección 6.3.2. En este caso, una disminución de\(E\) hace que la\(-1/G_D(E)\) curva se encuentre a la izquierda de la\(a(j\omega)\) curva, y así los polos del sistema se muevan del eje imaginario al plano de la mitad izquierda como consecuencia de la perturbación. Se llega a la misma conclusión si consideramos la gráfica Nyquist para el sistema cuando la amplitud de\(v_A\) es\(10^{-4}\) voltio. La atenuación de ganancia del limitador desplaza entonces la curva de la Figura 6.17 hacia abajo para que el punto correspondiente a\(\omega = 50\) radianes por segundo intersecta el punto - 1. Una disminución incremental en\(E\) mueve la curva ligeramente hacia arriba, y el diagrama Nyquist resultante es el de un sistema estable.

Razonamiento similar muestra que un pequeño aumento en la amplitud en la intersección inferior conduce a mayores aumentos en la amplitud. Siguiendo este tipo de perturbación, el sistema finalmente logra el ciclo límite de amplitud estable implícito por la intersección superior con\(\omega \simeq 1.8\) radianes por segundo y\(E \simeq 0.73\) voltios. (El lector debe convencerse de que la intersección superior satisface las condiciones para un ciclo de límite de amplitud estable).

Cabe señalar que el concepto de comportamiento condicionalmente estable ayuda a comprender el rendimiento de señal grande de los sistemas para los que el desplazamiento de fase se aproxima pero no excede\(-180^{\circ}\) muy por debajo del crossover, y luego se recupera a un valor más razonable en el cruce. Si bien estos sistemas pueden exhibir un excelente rendimiento para niveles de señal que limitan el funcionamiento a la región lineal, el rendimiento generalmente se deteriora drásticamente cuando algún elemento en el bucle se satura. Por ejemplo, la recuperación de este tipo de sistema después de una etapa de gran amplitud puede incluir una serie de sobreimpulsos de señal grande, incluso si la respuesta de paso de señal pequeña del sistema es aproximadamente de primer orden.

Si bien un análisis detallado de dicho comportamiento está fuera del alcance de este libro, en el Capítulo 13 se incluyen ejemplos del desempeño de señales grandes de sistemas que se acercan a la estabilidad condicional.

Compensación no lineal

Como podríamos sospechar, las técnicas para compensar sistemas no lineales utilizando redes compensadoras lineales o no lineales no son particularmente bien entendidas. El método de elección suele depender críticamente de los detalles exactos de los elementos lineales y no lineales incluidos en el bucle. En algunos casos, el análisis de la función descriptora es útil para indicar enfoques de compensación, ya que los sistemas con mayor separación entre las\(- 1/G_D(E)\) curvas\(a(j\omega)\) y son generalmente relativamente más estables. En esta sección se describe un método específico para la compensación de sistemas no lineales.

Como se mencionó anteriormente, las transmisiones de bucle de rolloff rápido se utilizan debido a las grandes magnitudes que pueden producir en frecuencias intermedias. Desafortunadamente, si el desplazamiento de fase de este tipo de transmisión de bucle cae por debajo\(-180^{\circ}\) a una frecuencia donde su magnitud excede a uno, puede resultar estabilidad condicional. La compensación no lineal se puede utilizar para eliminar la posibilidad de oscilaciones en ciertos sistemas con este tipo de transmisión en bucle.

Como ejemplo, considere un sistema con una transmisión de bucle de región lineal

\[-L(s) = \dfrac{200}{(s + 1)(10^{-3} s + 1)^2}\label{eq6.3.26} \]

Esta transmisión de bucle tiene un desplazamiento de fase monótonamente decreciente en función del aumento de la frecuencia, y exhibe un margen de fase de aproximadamente\(65^{\circ}\). En consecuencia, la estabilidad incondicional se asegura incluso cuando algún elemento en el bucle se satura.

En un intento de mejorar la desensitividad del sistema, la compensación de serie que consiste en ganancia y dos funciones de transferencia de retardo podría agregarse a la transmisión en bucle de la ecuación\(\ref{eq6.3.26}\), lo que lleva a la transmisión de bucle modificada

\[-L'(s) = \left [\dfrac{200}{(s + 1)(10^{-3} s + 1)^2} \right ] \left [\dfrac{2.5 \times 10^3 (0.02s + 1)^2}{(s + 1)^2} \right ] \label{eq6.3.27} \]

Esta transmisión en bucle es, por supuesto, la utilizada para ilustrar la posibilidad de estabilidad condicional (Ecuación\(\ref{eq6.3.23}\)).

Figura 6.19 Red compensadora no lineal.

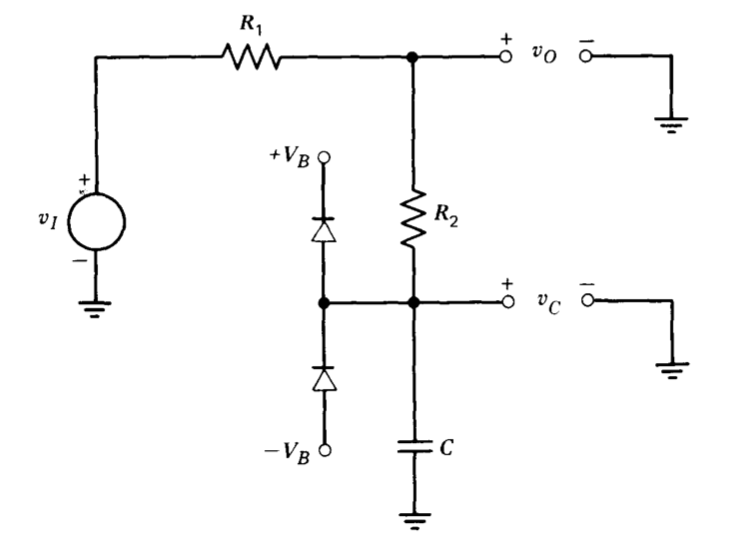
Considerar el efecto de implementar una o ambas funciones de transferencia de retraso con una red del tipo mostrado en la Figura 6.19. Si la magnitud del voltaje\(v_c\) es menor que\(V_B\), los diodos no conducen y la función de transferencia de la red es

\[\dfrac{V_o (s)}{V_i (s)} = \dfrac{R_2Cs + 1}{(R_1 + R_2)Cs + 1} \nonumber \]

Los valores de los elementos se pueden seleccionar para producir los parámetros de retraso incluidos en la Ecuación\(\ref{eq6.3.27}\).

La tensión de polarización\(V_B\) se elige para que cuando la señal aplicada a la red sea la que existe cuando el bucle oscila, los diodos recorten la tensión del condensador durante la mayor parte del ciclo. Bajo estas condiciones, la ganancia de la red no lineal (en un sentido de función de descripción) es

\[\dfrac{v_O}{v_I} \simeq \dfrac{R_2}{R_1 + R_2} \nonumber \]

Tenga en cuenta que si ambas funciones de transferencia de retardo se realizan de esta manera, la transmisión de bucle se puede hacer para convertir automáticamente de la dada por la ecuación\(\ref{eq6.3.27}\) a la de la ecuación\(\ref{eq6.3.26}\) en condiciones de inestabilidad inminente. Este tipo de compensación puede eliminar la posibilidad de un rendimiento condicionalmente estable en ciertos sistemas. Los niveles de señal que causan saturación también eliminan las funciones de retardo, y así se puede eliminar la posibilidad de inestabilidad.

PROBLEMAS

Ejercicio\(\PageIndex{1}\)

Figura 6.20 Elementos no lineales. (\(a\)) Limitador. (\(b\)) Zona muerta.

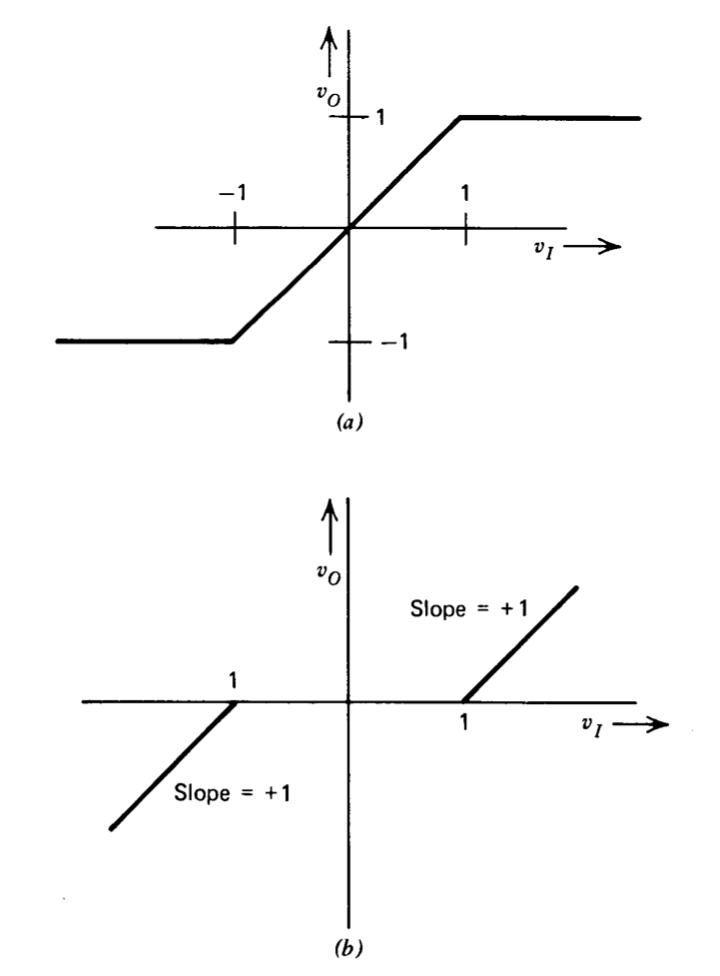
Una de las dificultades que implica analizar sistemas no lineales es que el orden de los elementos no lineales en un diagrama de bloques es importante. Demostrar esta relación comparando las características de transferencia que resultan cuando los dos elementos no lineales mostrados en la Figura 6.20 se utilizan en el orden\(ab\) con las características de transferencia que resultan cuando se cambia el orden a\(ba\).

Ejercicio\(\PageIndex{2}\)

Figura 6.21 Servomecanismo posicional.

Los resolutores son esencialmente transformadores variables que se pueden utilizar como transductores de ángulo mecánico. Cuando dos de estos dispositivos se utilizan en un servomecanismo, la tensión obtenida del par es una función sinusoidal de la diferencia entre los ángulos de entrada y salida del sistema. En la Figura 6.21 se muestra un modelo para un servomecanismo utilizando resolvers.

(a) El voltaje aplicado a la combinación amplificador-motor es cero para\(\theta_O - \theta_I = n \pi\), donde\(n\) es cualquier entero. Utilizar el análisis linealizado para determinar cuáles de estos puntos de equilibrio son estables.

b) El sistema es accionado a una velocidad de entrada constante de 7 radianes por segundo. ¿Cuál es el error de estado estacionario entre la salida y la entrada para esta excitación?

c) La tasa de entrada se cobra de 7 a 7.1 radianes por segundo en tiempo cero. Encuentre el transitorio de ángulo de salida correspondiente.

Ejercicio\(\PageIndex{3}\)

Figura 6.22 Circuito de enraizamiento cuadrado.

Un divisor analógico fue descrito en la Sección 6.2.2. Supongamos que la función de transferencia del amplificador operacional mostrado en la Figura 6.2 es

\[a(s) = \dfrac{3 \times 10^5}{(s + 1)(10^{-5} s + 1)^2 \nonumber \]

¿El divisor es estable en el rango de entradas\(-10 < v_A < + 10\)\(0 < v_B < +10\)?

En la Figura 6.22 se muestra un circuito de enraizamiento cuadrado que utiliza una técnica similar a la del divisor. ¿Cuál es la relación entrada-salida ideal para este circuito? Determinar el rango de voltajes de entrada para los cuales el rooter cuadrado es estable, asumiendo que\(a(s)\) es como se ha dado anteriormente.

Ejercicio\(\PageIndex{4}\)

Figura 6.23 Péndulo invertido

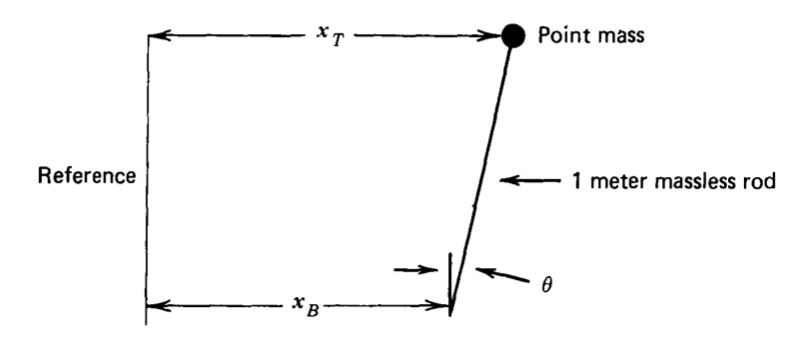
La Figura 6.23 define variables que pueden ser utilizadas para describir el movimiento de un péndulo invertido. Determinar una función de transferencia que relaciona el ángulo 0 con la posición\(x_B\), que es válida para valores pequeños de\(\theta\). Pista. Puede encontrar que una manera relativamente fácil de obtener la función de transferencia requerida es usar las dos ecuaciones simultáneas (o el diagrama de bloques correspondiente) que se\(x_T\) relacionan con\(\theta\) y\(\theta\) con\(x_B\) y\(x_T\).

Supongamos que eres capaz de conducir en\(x_T\) función de\(\theta\). Encontrar una función de transferencia,\(X_t(s)/\theta (s)\), tal que el péndulo invertido se estabilice.

Ejercicio\(\PageIndex{5}\)

Figura 6.24 Red de diodo-condensador.

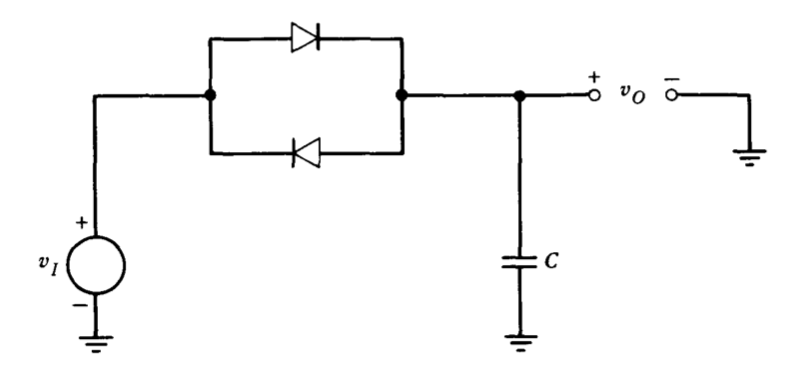
En la Figura 6.24 se muestra una red de diodo-condensador. Trazar el voltaje de salida que resulta para una señal de entrada de onda sinusoidal con un valor pico de\(E\). Puede suponer que los diodos tienen un umbral ideal de 0.5 voltios (es decir, sin conducción hasta que se alcance un voltaje de polarización directa de 0.5 voltios, cualquier corriente directa posible sin aumentar el voltaje del diodo por encima de 0.5 voltios). Evaluar la magnitud y el ángulo de\(G_D(1)\) para esta red. (Puedes, por supuesto, hacer ejercicio\(G_D (E)\) en general si lo deseas, pero es una expresión relativamente involucrada.)

Ejercicio\(\PageIndex{6}\)

Figura 6.25 Relación de transferencia no lineal.

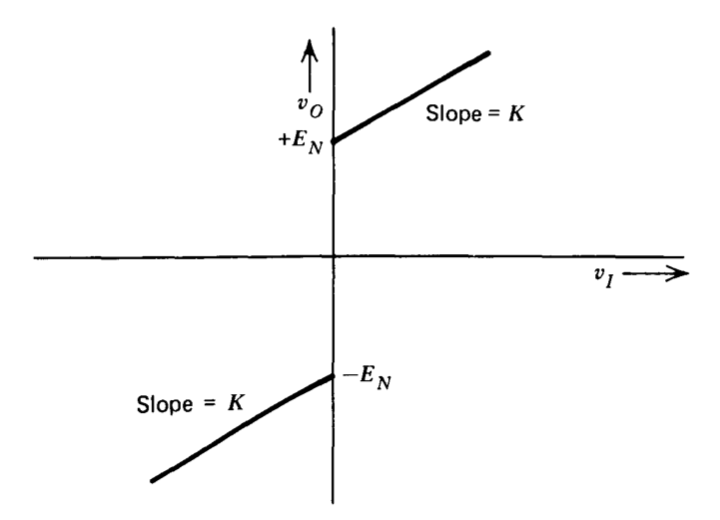
Determinar la función de descripción para un elemento con las características de carbón de transferencia que se muestran en la Figura 6.25.

Ejercicio\(\PageIndex{7}\)

Figura 6.26 Oscilador no lineal.

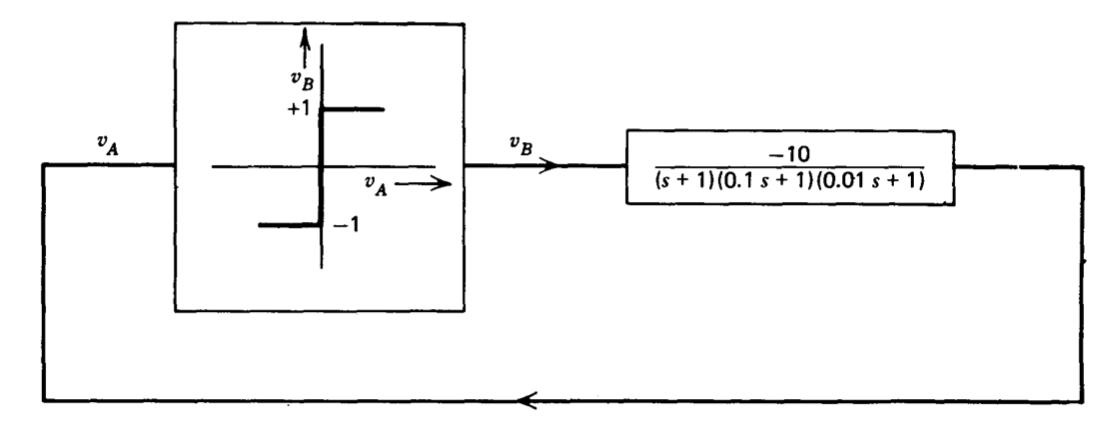
Analizar el bucle mostrado en la Figura 6.26. En particular, encontrar la frecuencia de oscilación y estimar los niveles de las señales\(v_A\) y\(v_B\). También calcule la relación del tercer armónico al primer armónico en la entrada al no lineal

Ejercicio\(\PageIndex{8}\)

Figura 6.27 Sistema no lineal.

¿Puede el sistema mostrado en la Figura 6.27 producir un ciclo de límite de amplitud estable? Explique.

Ejercicio\(\PageIndex{9}\)

Encuentre una función de transferencia que, cuando se combina con un limitador, pueda producir ciclos de límite de amplitud estable en dos frecuencias diferentes. Diseñe una red de amplificador operacional que realice su función de transferencia.

Ejercicio\(\PageIndex{10}\)

Figura 6.28 Características de transferencia del controlador

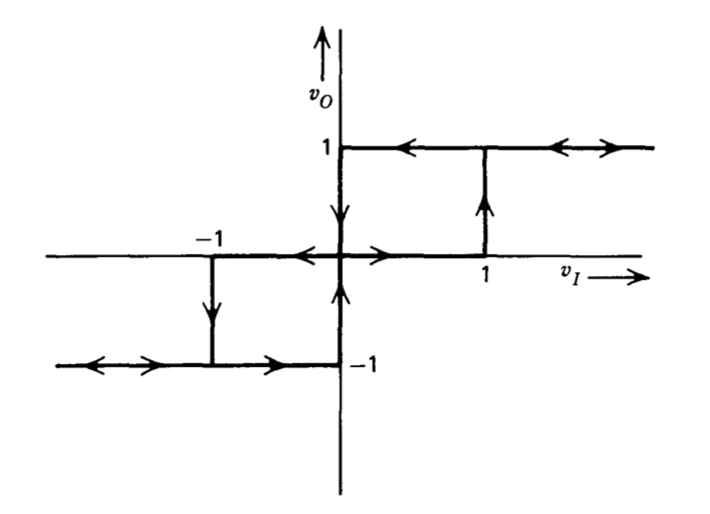
Las características de transferencia para un controlador de tipo relé de tres estados se ilustran en la Figura 6.28.

(a) Demostrar que la función que describe para este elemento es

\[G_D (E) = \dfrac{2}{\pi E} \sqrt{2 + 2\sqrt{1 - \dfrac{1}{E^2}}} \measuredangle -\tan^{-1} \dfrac{1}{E \left (1 + \sqrt{1 - \dfrac{1}{E^2}} \right )}\nonumber \]

(b) El controlador se combina en un bucle de retroalimentación negativa con elementos lineales con una función de transferencia

\[a(s) = \dfrac{a_0}{(s + 1)(0.1s + 1)}\nonumber \]

¿Cuál es el rango de valores\(a_0\) para una operación estable?

(c) Para\(a_0\) que sea el doble del valor crítico, encuentre la amplitud del componente fundamental de la señal aplicada al controlador.

Ejercicio\(\PageIndex{11}\)

Figura 6.29\(R-L-C\) oscilador.

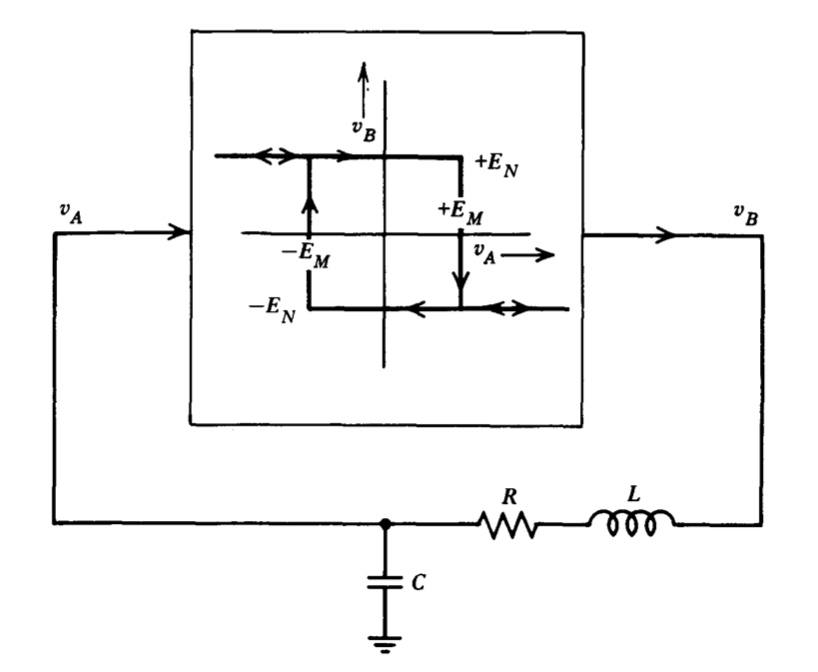
Una posible configuración para un oscilador sinusoidal combina un disparador Schmitt con un\(R-L-C\) circuito como se muestra en la Figura 6.29. Encuentre la relación entre\(E_M\)\(E_N\), y la relación de amortiguación de la red que asegura que se puedan mantener las oscilaciones. (Puede asumir una carga insignificante en la entrada y salida del disparador Schmitt).

Ejercicio\(\PageIndex{12}\)

Tres valores de transmisión en bucle, dados por Ecuaciones\(\ref{eq6.3.23}\)\(\ref{eq6.3.24}\), y\(\ref{eq6.3.26}\) fueron considerados como parte de la discusión de sistemas condicionalmente estables. Supongamos que se construyen tres sistemas de retroalimentación negativa con\(f(s) = 1\) transmisiones de bucle dadas por las expresiones a las que se hace referencia anteriormente. Comparar el rendimiento calculando los tres primeros coeficientes de error para cada uno de los tres sistemas.