7.2: Deriva referida a la Entrada
- Page ID
- 84311
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
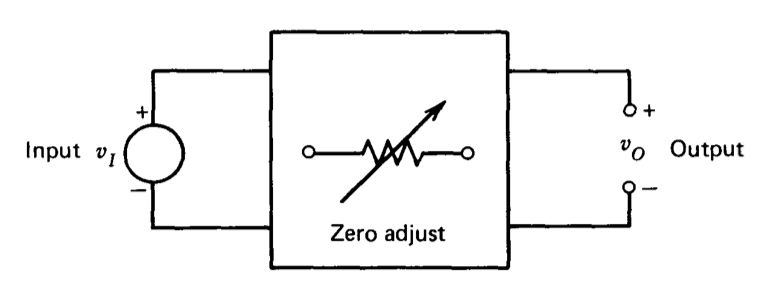
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)La medida más útil de la deriva de un amplificador es una cantidad llamada deriva referida a la entrada, y a menos que se indique específicamente lo contrario, esta cantidad es la implícita cuando se usa el término deriva. Deriva referida a la entrada se define con referencia a la Figura 7.1. Esta figura muestra un amplificador con un voltaje de salida deseado supuesto de cero para voltaje de entrada cero. El amplificador se equilibra inicialmente haciendo\(v_I = 0\), y ajustando algún parámetro del amplificador (mostrado diagramáticamente en la Figura 7.1 como una resistencia variable) hasta\(v_O = 0\). Luego se cambia una cantidad externa, como temperatura, voltaje de suministro o tiempo y, si el amplificador es sensible a esta cantidad, su voltaje de salida cambia. Luego se aplica una tensión de entrada al amplificador, y\(v_I\) se ajusta hasta que vo nuevamente sea igual a cero. La deriva referida a la entrada del amplificador es igual al valor de\(v_I\) necesario para poner a cero la salida. La magnitud resultante suele normalizarse y especificarse, por ejemplo, como voltios por grado centígrado, voltios por voltio (de voltaje de alimentación) o voltios por semana. El aspecto de señal mínima detectable de esta definición es evidente por sí mismo.
En muchas situaciones nos preocupa no sólo la variabilidad del circuito ya que se cambia algún factor de influencia externo, sino también por las incertidumbres que surgen del proceso de fabricación. En estos casos, en lugar de equilibrar inicialmente el circuito, el voltaje que debe aplicarse a su entrada para hacer que su salida sea cero puede especificarse como el desplazamiento referido a la entrada. Las especificaciones relacionadas con la deriva y el desplazamiento se combinan a veces enumerando el desplazamiento máximo de entrada que resultará de las variaciones de fabricación y en un rango de condiciones de operación.
Existe una tendencia a utilizar una definición alternativa (incorrecta) de deriva, que implica dividir la deriva medida en la salida del amplificador por la ganancia del amplificador. La dificultad en este enfoque surge ya que la ganancia suele depender de la variable estimulante de la deriva.
Si bien las mediciones alternativas de deriva o desplazamiento pueden ser equivalentes en casos especiales, y a menudo se utilizan en el laboratorio para simplificar un procedimiento de medición, es necesario asegurar la equivalencia de otros métodos para cada circuito. Normalmente utilizaremos las definiciones originales para nuestros cálculos.
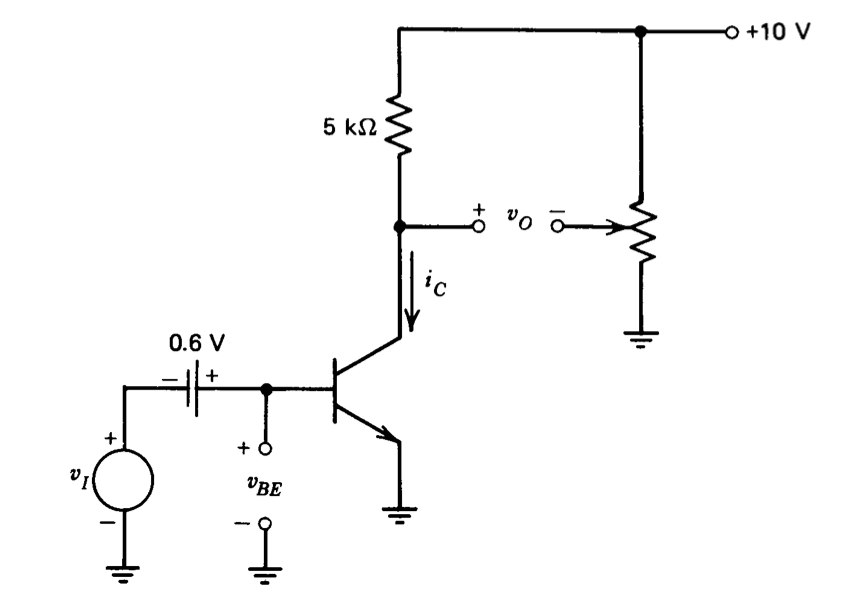
La Figura 7.2 muestra un amplificador muy simple, que se utilizará para ilustrar cálculos de deriva y para determinar cómo cambia la tensión de base a emisor de un transistor bipolar con la temperatura. Se supone que se requiere la deriva del circuito con respecto a la temperatura, y que la temperatura inicial es\(300^{\circ}\ K\). Se supone además que para el transistor utilizado,\(i_C = 1\ mA\) at\(v_{BE} = 0.6\ V\) y\(T = 300^{\circ}\ K\). Con\(v_I = 0\), estos parámetros muestran que es necesario ajustar el potenciómetro a su posición media para hacer\(v_O = 0\). Luego se cambia la temperatura a\(301^{\circ}\ K\), y se observa que\(v_O\) es negativa. (El monto no es importante para nuestros fines.) Para volver\(v_O\) a cero (requerido por nuestra definición de deriva), es necesario devolver la corriente del colector del transistor a su valor original. El cambio en\(v_{BE}\) requerido para restaurar la corriente del colector es idénticamente igual al cambio requerido en\(v_I\) y es por lo tanto, por definición, la deriva referida a la entrada del amplificador. Esta discusión muestra que la deriva para este circuito puede ser evaluada determinando cómo\(v_{BE}\) debe variar con la temperatura para mantener constante la corriente del colector.
La deriva para el circuito mostrado en la Figura 7.2 se puede determinar a partir de la relación entre las variables terminales del transistor y la temperatura. Si las caídas óhmicas son insignificantes y la corriente del colector es grande en comparación con la corriente de saturación\(I_S\) (P. E. Gray et al., Physical Electronics and Models of Transistors, Wiley, Nueva York, 1964.)
\[i_C = I_S e^{qv_{BE}/kT} = AT^3 e^{qV_{go}/kT} e^{qV_{BE}/kT} = AT^3 e^{q(v_{BE} - V_{go})/kT}\label{eq7.2.1} \]
donde\(A\) es una constante dependiente del tipo de transistor y geometría,\(q\) es la carga en un electrón,\(k\) es la constante de Boltzmann,\(T\) es la temperatura, y\(V_{go}\) es el ancho del espacio de energía extrapolado a cero absoluto dividido por la carga de electrones (\(V_{go} = 1.205\)voltios para silicio). (Existe desacuerdo entre los autores sobre el exponente de\(T\) en Ecuación\(\ref{eq7.2.1}\), con valores algo menores utilizados en algunos desarrollos. Como veremos, la cantidad tiene relativamente poco efecto sobre el resultado final. (El exponente aparece únicamente como factor multiplicador en el término final de la Ecuación\(\ref{eq7.2.5}\) y como coeficiente en la Ecuación\(\ref{eq7.2.8}\)). Además, dos transistores similares deben tener valores estrechamente emparejados para este exponente, y el grado de coincidencia entre un par es la cantidad más importante en las aplicaciones anticipadas). Es posible verificar la dependencia exponencial de la corriente del colector en el voltaje de base a emisor experimentalmente durante aproximadamente nueve décadas de corriente de funcionamiento para muchos transistores modernos.
Resolución de ecuaciones\(\ref{eq7.2.1}\) para\(v_{BE}\) rendimientos
\[v_{BE} = \dfrac{kT}{q} \ln \dfrac{i_C}{AT^3} + V_{go}\label{eq7.2.2} \]
La derivada parcial de\(v_{BE}\) con respecto a la temperatura a constante\(i_C\) es la relación deseada, y
\[\left.\dfrac{\partial v_{BE}}{\partial T}\right|_{i_C = \text{const}} = \dfrac{k}{q} \ln \dfrac{i_C}{AT^3} - \dfrac{3k}{q}\label{eq7.2.3} \]
Sin embargo, de la ecuación\(\ref{eq7.2.2}\)
\[\dfrac{k}{q} \ln \dfrac{i_C}{AT^3} = \dfrac{v_{BE} - V_{go}}{T}\label{eq7.2.4} \]
Sustitución de\(\ref{eq7.2.3}\) rendimientos de ecuación\(\ref{eq7.2.4}\) en ecuación
\[\left.\dfrac{\partial v_{BE}}{\partial T}\right|_{i_C = \text{const}} = \dfrac{v_{BE} - V_{go}}{T} - \dfrac{3k}{q}\label{eq7.2.5} \]
La cantidad\(v_{BE} - V_{go}/T\) es\(-2mV/ ^{\circ} C\)\(T = 300 ^{\circ} K\) para el\(v_{BE}\) valor típico de 0.6 voltios. El término\(3k/q = 0.26 mV/ ^{\circ} C\); por lo tanto, a un buen grado de aproximación
\[\left.\dfrac{\partial v_{BE}}{\partial T}\right|_{i_C = \text{const}} \simeq \dfrac{v_{BE} - V_{go}}{T}\label{eq7.2.6} \]
La aproximación de Ecuación\(\ref{eq7.2.6}\) vincula los dos valores de regla general de\(0.6 V\) y\(-2 mV/ ^{\circ} C\) para la dependencia de la magnitud y la temperatura, respectivamente, de la tensión directa de una unión de silicio.
Es valioso señalar dos relaciones que se explotan en el diseño de amplificadores d-c de transistor. Primero, sin aproximaciones más allá de las implícitas por la ecuación\(\ref{eq7.2.1}\), es posible determinar la variación de voltaje de base a emisor de transistor requerida para la corriente de colector constante conociendo solo el voltaje, la temperatura y el material utilizado para fabricar el transistor. Además, si dos transistores de silicio (o dos germanio) tienen voltajes de base a emisor idénticos a una temperatura y a ciertas corrientes de funcionamiento (no necesariamente idénticas), los coeficientes de temperatura de los voltajes de base a emisor deben ser iguales. En segundo lugar, el coeficiente de temperatura de base a emisor en cualquier corriente de funcionamiento es casi independiente de la temperatura como se muestra en el siguiente desarrollo. La variación del coeficiente de temperatura con la temperatura se encuentra diferenciando la ecuación\(\ref{eq7.2.5}\) con respecto a la temperatura, rindiendo
\[\dfrac{\partial}{\partial T} \left [ \dfrac{\partial v_{BE}}{\partial T} \right ]_{i_C = \text{const}} = \dfrac{-(v_{BE} - V_{go}) + T(\partial v_{BE}/\partial T)}{T^2}\label{eq7.2.7} \]
Sustituyendo\(\ref{eq7.2.5}\) por el\(\partial v_{BE}/\partial T\) término en Ecuación\(\ref{eq7.2.7}\), obtenemos
\[\dfrac{\partial}{\partial T} \left ( \dfrac{\partial v_{BE}}{\partial T} \right ) = -3k/qT\label{eq7.2.8} \]
Evaluando la Ecuación\(\ref{eq7.2.8}\) en\(300^{\circ} K\) muestra que la magnitud del cambio en el coeficiente de temperatura de voltaje de base a emisor con temperatura es menor que\(1 \mu V/ ^{\circ} C\). (Un interesante desarrollo alternativo de esta relación se da en “Una expresión exacta para la variación térmica del voltaje base del emisor de transistores bipolares”, R. J. Widlar, National Semiconductor Corp., Documento Técnico TP-1, marzo de 1967.)
Ahora es posible determinar la deriva referida a la entrada de nuestro amplificador original. Para volver\(v_O\) en la Figura 7.2 a cero a la temperatura elevada, es necesario disminuir\(i_C\) a su valor original de\(1\ mA\), y esta disminución requiere un\(-2.26\ mV\) cambio en\(v_I\) (Ecuación\(\ref{eq7.2.5}\)). La deriva referida a la entrada de nuestro amplificador es por definición\(-2.26\ mV/ ^{\circ} C\), y la ecuación\(\ref{eq7.2.8}\) asegura que esta deriva es esencialmente constante en un amplio rango de temperaturas.


