7.3: El amplificador diferencial

El coeficiente de temperatura altamente predecible de la tensión de base a emisor de un transistor bipolar ofrece la posibilidad de que se pueda usar algún tipo de compensación para producir amplificadores de baja deriva. Es evidente que el uso de una unión de transistores para compensar las variaciones de voltaje de una segunda unión similar debería proporcionar excelentes resultados ya que ambos dispositivos varían de manera similar. En esta sección se describe una conexión que explota el

características de un par de transistores bipolares para proporcionar baja deriva combinada con varias otras características útiles.

Topología

Figura 7.3 Circuito que ilustra el desarrollo del amplificador diferencial.

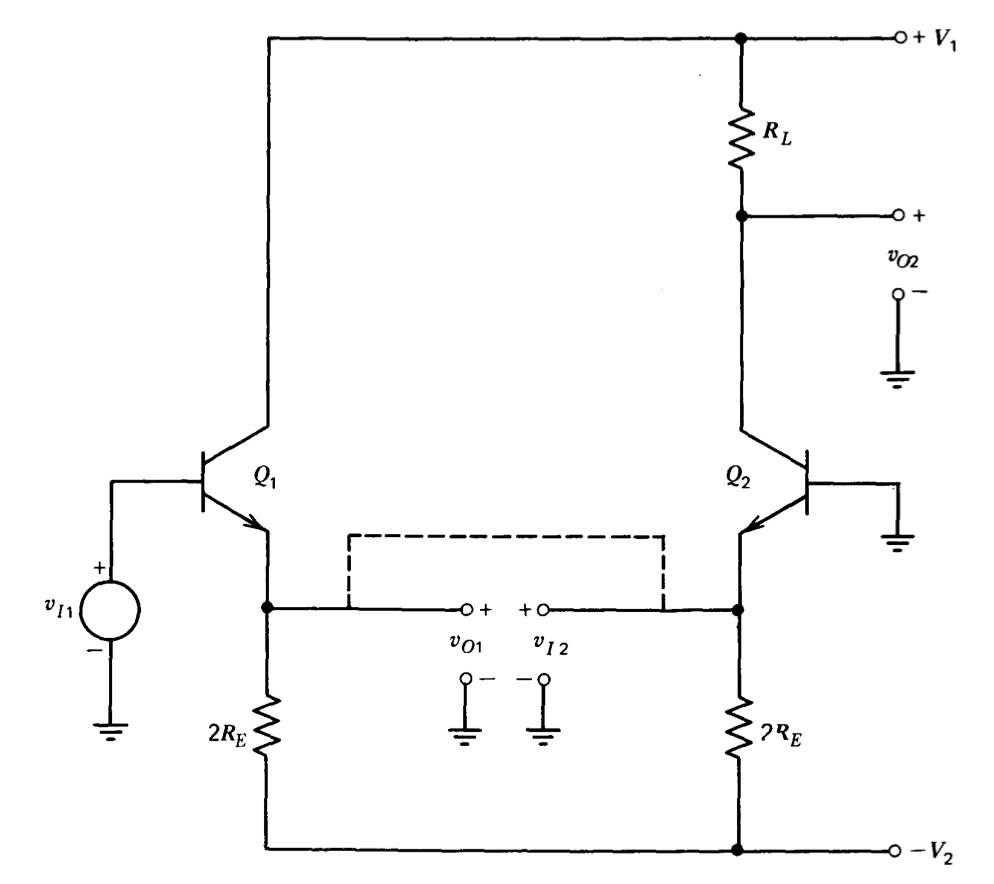
Considera la conexión que se muestra en la Figura 7.3. Aquí el transistor\(Q_2\) está conectado como un amplificador de base común, mientras que el transistor\(Q_1\) está conectado como seguidor de emisor. Supongamos que inicialmente\(v_{I1} = 0\), que los dos transistores están a la misma temperatura y que están emparejados en el sentido de que tienen corrientes de saturación idénticas. En este caso los voltajes en los emisores de los dos transistores serán iguales, o\(v_{O1} = v_{I2}\). La conexión que se muestra como una línea punteada se puede completar sin cambios en ningún nivel de voltaje. Si la magnitud de la tensión\(V_2\) es mucho mayor que las variaciones anticipadas en la tensión de base a emisor, la combinación de resistencias de corriente a través de paralelo es prácticamente independiente de la temperatura. Las características del transistor coincidente aseguran que esta corriente constante se divida por igual entre los dos transistores. Si también asumimos que la ganancia de corriente de base común del transistor\(Q_2\) es una, los cambios de temperatura resultan en cambios insignificantes en la corriente del colector de este dispositivo. Así, la deriva referida a la entrada de esta conexión puede ser cercana a cero. Además de proporcionar compensación de temperatura, la ganancia de corriente y la resistencia de entrada del transistor\(Q_1\) aumenta la resistencia de entrada del circuito por un factor\(2\beta\) superior al visto en el emisor de\(Q_2\).

El circuito que resulta cuando se completa la conexión punteada en la Figura 7.3 se muestra en la Figura 7.4. La simetría inherente del amplificador diferencial se ha enfatizado al incluir una resistencia colector-carga para\(Q_1\) y permitiendo que las señales de entrada se apliquen a cualquiera de las bases. Una segunda señal de salida se indica entre los colectores de los dos transistores en la Figura 7.4, de manera que están disponibles tanto salidas diferenciales (entre colector) como salidas de un solo extremo (ya sea colector a tierra).

Ganancia

Figura 7.4 El amplificador diferencial.

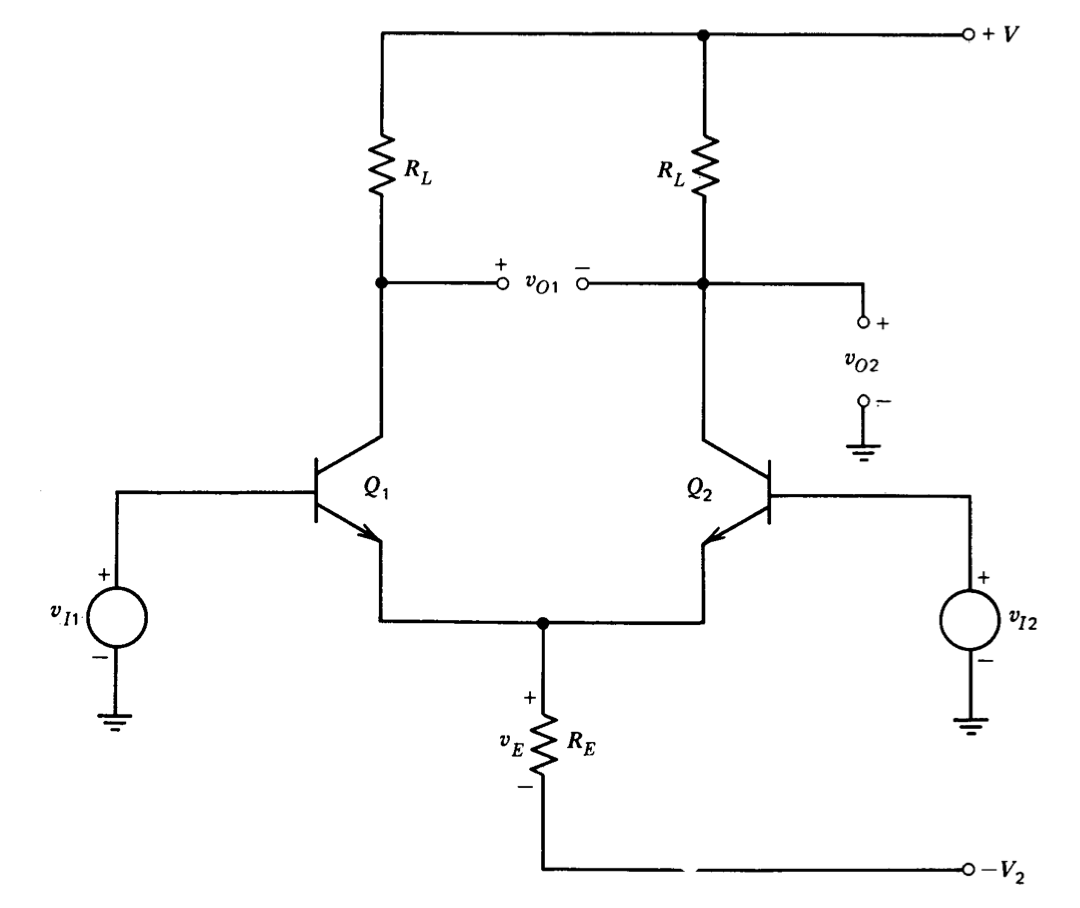
La salida del circuito de la Figura 7.4 para cualquier voltaje de entrada particular se puede calcular por los métodos habituales. Sin embargo, se dispone de una técnica analítica alternativa y útil (se da un análisis esencialmente idéntico para amplificadores diferenciales de tubo de vacío en T. S. Gray, Applied Electronics, 2nd Ed., Wiley, Nueva York, 1954, páginas 504-509.) que simplifica los cálculos y da una mayor comprensión de los mismos. el funcionamiento del circuito. La ganancia del circuito se calcula para dos tipos particulares de entradas, una entrada diferencial con\(v_{I1} = v_{I2}\), y una entrada de modo común con\(v_{I1} = v_{I2}\).

Figura 7.5 Modelo incremental para un amplificador diferencial.

Figura 7.6 Medio circuito derecho para una entrada diferencial.

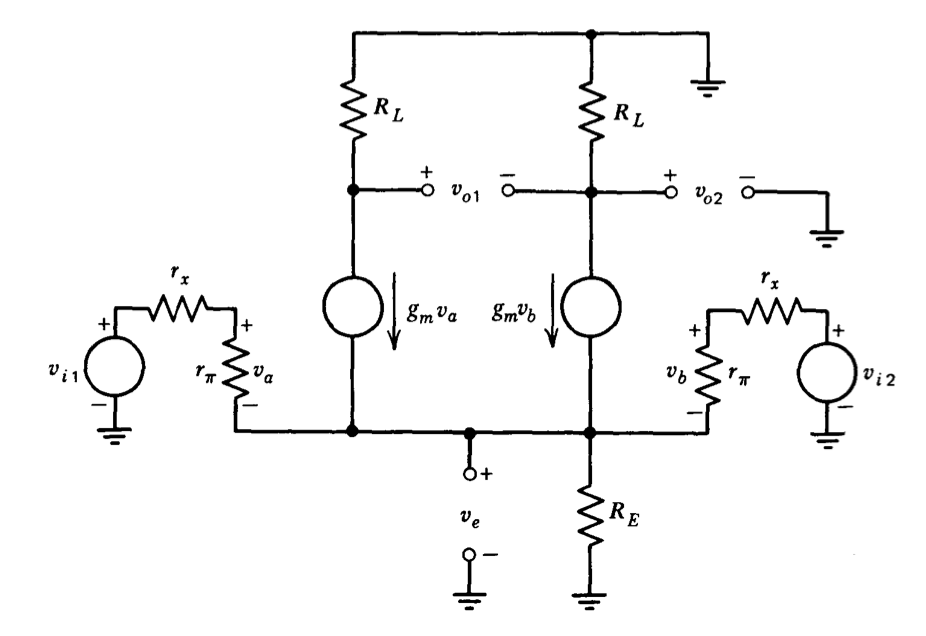
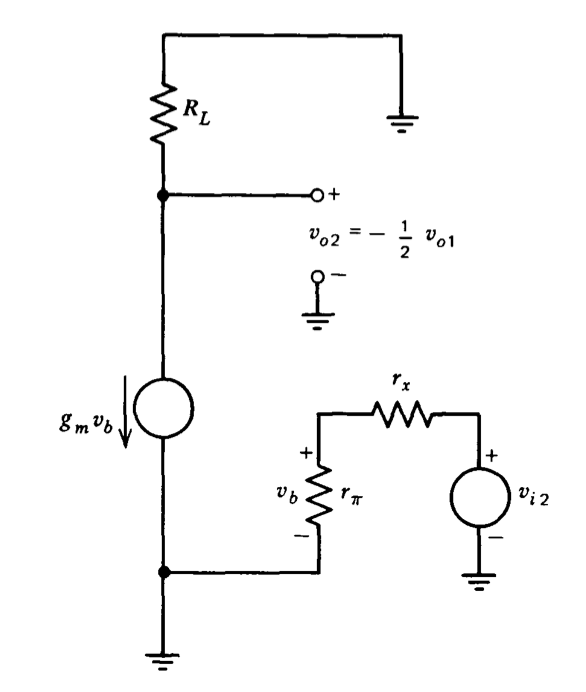
La Figura 7.5 muestra un esquema donde los transistores han sido reemplazados por modelos de circuito apropiados e idénticos. Considerar inicialmente una entrada diferencial pura, de tamaño suficientemente pequeño para que el modelo de región lineal siga siendo válido. Se demuestra fácilmente que en este caso el voltaje ve no cambia y que la conexión común del emisor, por lo tanto, puede considerarse un punto de conexión a tierra incrementalmente. El modelo incremental para cualquiera de los dos medios circuitos se reduce al que se muestra en la Figura 7.6. La ganancia incremental a la salida de un solo extremo\(v_{o2}\),, es simplemente la de un amplificador de emisor común:

\[\dfrac{v_{o2}}{v_{i2}}|_{v_{i1} = -v_{i2}} = \dfrac{-g_m R_L r_{\pi}}{r_x + r_{\pi}} \nonumber \]

El componente de salida diferencial de\(v_{o1}\) para el medio circuito izquierdo es idéntico en magnitud pero opuesto en signo al del medio circuito derecho; por lo tanto,\(v_{o2} = -\tfrac{1}{2} v_{o1}\). La ganancia incremental a una salida diferencial es entonces

\[\dfrac{v_{o1}}{v_{i2}}|_{v_{i1} = -v_{i2}} = \dfrac{2g_m R_L r_{\pi}}{r_x + r_{\pi}} \nonumber \]

Es convencional considerar ganancias calculadas para una señal de entrada diferencial aplicada entre dos bases del amplificador, en lugar de asumir una señal aplicada a una base y su negativo aplicado a la otra. Si la señal entre las bases es que\(e_d = 2 v_{i1} = - 2 v_{i2}\) las ganancias se convierten

\[\dfrac{v_{o2}}{e_d} = \dfrac{g_m R_L r_{\pi}}{2(r_x + r_{\pi})}\label{eq7.3.3} \]

y

\[\dfrac{v_{o1}}{e_d} = \dfrac{-g_m R_L r_{\pi}}{r_x + r_{\pi}} \nonumber \]

Figura 7.7 Modelo de circuito para entradas de modo común.

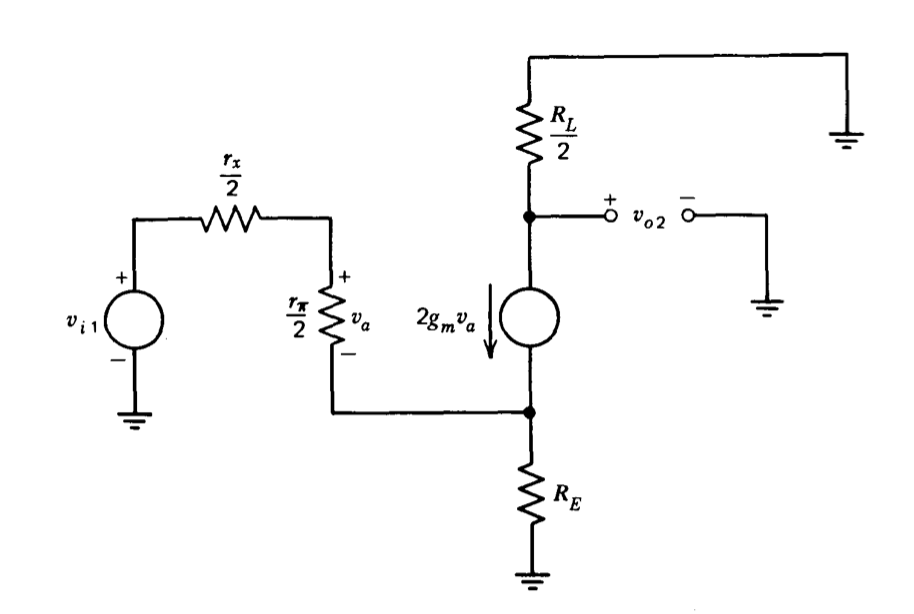
Para una entrada de modo común pura el voltaje (\(v_{i1} = v_{i2}\)), la simetría asegura que el voltaje\(v_{o1}\) (Figura 7.5) permanezca cero y eso\(v_a = v_b\). Por lo tanto, es posible “doblar” el circuito alrededor de su línea media vertical y sus componentes correspondientes paralelos. El modelo incremental resultante se muestra en la Figura 7.7. La ganancia a una salida de un solo extremo es idéntica a la de un amplificador de emisor común con degeneración de emisor:

\[\dfrac{v_{o2}}{v_{i1}}|_{v_{i1} = v_{i2}} = \dfrac{-g_mR_L r_{\pi}}{2[r_{\pi}/2 + r_x/2 + (\beta + 1)R_E]}\label{eq7.3.5} \]

La ganancia de entrada de modo común a salida diferencial es cero ya que\(v_{o1}\) no cambia en respuesta a una señal de entrada de modo común.

Si bien la ganancia del amplificador diferencial se ha calculado solo para dos tipos específicos de señales de entrada, cualquier entrada puede descomponerse en una suma de señales diferenciales y de modo común. Se puede calcular la salida a cada componente individual y, debido a la linealidad, la salida es la suma de las respuestas a las dos entradas individuales. Por ejemplo, asuma entradas\(e_a\) y se\(e_b\) aplican a las entradas izquierda y derecha del circuito, respectivamente. La descomposición produce un componente\(e_{cm} = (e_a + e_b)/2\) de modo común y un componente diferencial (aplicado entre entradas)\(e_d = e_a - e_b\). La implicación física es clara. Se supone que cualquier combinación de niveles de voltaje de entrada es en realidad la suma de dos señales: una señal de modo común (las dos bases se incrementan en cantidades iguales) igual al nivel promedio, y una señal diferencial (las dos bases se incrementan por señales de igual magnitud, polaridad opuesta) igual a la voltaje aplicado entre entradas.

Relación de rechazo de modo común

La evolución del nombre amplificador diferencial es evidente cuando nos damos cuenta de que los valores de los elementos del circuito suelen ser tales que la ganancia a una señal diferencial es significativamente mayor que la de una señal de modo común. La relación de ganancia diferencial a ganancia de modo común se denomina relación de rechazo de modo común (\(\text{CMRR}\)), y muchas aplicaciones requieren alta\(\text{CMRR}\). Por ejemplo, un electrocardiograma es un registro de la señal que resulta a medida que el corazón se contrae, y es útil para el diagnóstico de ciertos tipos de enfermedades cardíacas. La señal deseada, detectada por medio de dos electrodos unidos al cuerpo, tiene una amplitud de aproximadamente 1 mV. Además de la señal deseada, un componente de ruido en la frecuencia de la línea eléctrica con una amplitud de hasta 0.1 voltios puede estar presente como una señal de modo común en ambos electrodos. Un amplificador con lo suficientemente alto se\(\text{CMRR}\) puede utilizar para separar la señal deseada del ruido interferente.

El análisis de la Sección 7.3.2 indica que la relación de rechazo en modo común de un amplificador diferencial con la salida tomada entre colectores debe ser infinita. (Como veremos, este resultado es consecuencia del modelo idealizado utilizado.) El\(\text{CMRR}\) para un amplificador diferencial de salida de un solo extremo se obtiene dividiendo la ecuación\(\ref{eq7.3.3}\) por la ecuación\(\ref{eq7.3.5}\) que produce la magnitud

\[\text{CMRR} = \dfrac{r_{\pi}/2 + r_x/2 + (\beta + 1) R_E}{r_{\pi} + r_x} \nonumber \]

Típicamente,\((\beta + 1) R_E \gg r_{\pi} \gg r_x\), para que

\[\text{CMRR} \simeq \dfrac{(\beta + 1) R_E}{r_{\pi}} \simeq g_m R_E\label{eq7.3.7} \]

Dado que la corriente de reposo a través\(R_E\) (Figura 7.4) es igual al doble de la corriente del emisor de cualquiera de los transistores, se\(\text{CMRR}\) puede relacionar con\(V_E\), el voltaje de reposo a través\(R_E\), por

\[\text{CMRR} = \dfrac{q}{kT} \dfrac{V_E}{2R_E} R_E \simeq 20 V_E\label{eq7.3.8} \]

Ecuación\(\ref{eq7.3.8}\)) muestra que una forma de lograr altas relaciones de rechazo de modo común para amplificadores diferenciales de salida de un solo extremo es usar un voltaje de polarización grande. Una alternativa atractiva (que permite un voltaje de alimentación más moderado) es el uso de una fuente de corriente (realizada con un transistor con degeneración de emisor) en lugar de\(R_E\). Este enfoque tiene la ventaja adicional de que el nivel de corriente de reposo es independiente de la señal de entrada de modo común, y por estas razones la mayoría de los amplificadores d-c de alto rendimiento incluyen una fuente de corriente de circuito emisor.

Figura 7.8 Circuito que ilustra el efecto\(r_{\mu}\) de desiguales

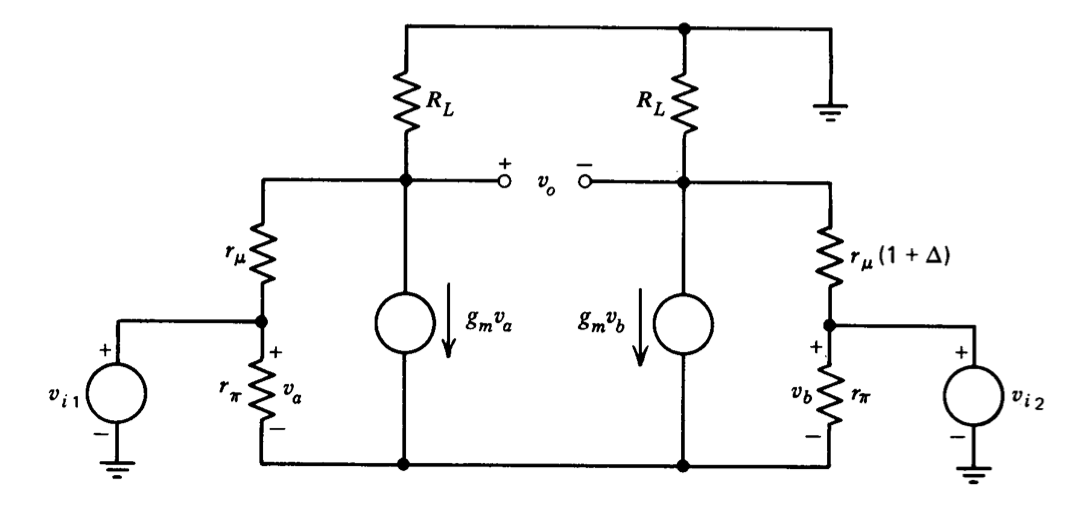
Si el modelo de transistor simplificado utilizado hasta ahora fuera estrictamente válido, el\(\text{CMRR}\) para un amplificador con una fuente de corriente de circuito emisor estaría en finito independientemente de si se utiliza una salida de un solo extremo o una salida diferencial, ya que la resistencia incremental de la fuente de corriente (que reemplaza \(R_E\)en Ecuación\(\ref{eq7.3.7}\)) es infinito. El análisis basado en un modelo más completo muestra que no es posible lograr infinito\(\text{CMRR}\) con una salida de un solo extremo, sino que se\(\text{CMRR}\) puede hacer arbitrariamente alta para un amplificador de salida diferencial al hacer coincidir todos los parámetros del transistor lo suficientemente cerca. Es útil para ilustrar la degradación que resulta del emparejamiento imperfecto con el ejemplo. La Figura 7.8 muestra un circuito equivalente de región lineal para un amplificador diferencial. Se ha incluido una resistencia de colector a base en el modelo de transistor. (También veremos que es necesaria una resistencia adicional entre colector y emisor para completar el modelo. Esta segunda resistencia se omite de la presente discusión ya que el modelo simplificado ilustra el punto adecuadamente). La razón física de la presencia de este elemento en el modelo se describe en la Sección 8.3.1. La magnitud de esta resistencia es\(r_{\mu}\) para un transistor, mientras que la del segundo dispositivo difiere en una fracción\(\Delta\). Todos los demás parámetros del circuito coinciden de manera idéntica. Se supone que\(r_x\) es despreciablemente pequeño en comparación con\(r_{\pi}\). (Esta suposición es frecuentemente válida en el análisis de amplificadores d-c porque los transistores suelen funcionar a corrientes bajas para disminuir la corriente de entrada y minimizar las compensaciones del autocalentamiento diferencial. La resistencia\(r_{\pi}\) crece aproximadamente inversamente con la corriente de colector, mientras que el valor de\(r_x\) está acotado, con un valor máximo habitual de 100 a 200\(\Omega\). Un valor típico\(r_{\pi}\) para transistores como el 2N5963 es 2.5 M\(\Omega\) a una corriente de funcionamiento de 10\(\mu A\).) Se supone además que el circuito se ha construido con una fuente de corriente de circuito emisor ideal. Dado que\(r_{\mu} \gg R_L\), la ganancia para una entrada diferencial es

\[\dfrac{v_o}{(v_{i2} - v_{i1})}|_{v_{i1} = -v_{i2}} = g_m R_L\label{eq7.3.9} \]

La ganancia para una entrada de modo común es

\[\dfrac{v_o}{v_{i1}}|_{v_{i1} = v_{i2}} = \dfrac{\Delta R_{\mu} R_L}{(R_L + r_{\mu}) [(1 + \Delta ) r_{\mu} + R_L]} \nonumber \]

Una vez más invocar la desigualdad\(r_{\mu} \gg R_L\) lleva a

\[\dfrac{v_o}{v_{i1}}|_{v_{i1} = v_{i2}} \simeq \dfrac{\Delta R_L}{(1 + \Delta ) r_{\mu}}\label{eq7.3.11} \]

El resultante\(\text{CMRR}\) se obtiene dividiendo la ecuación\(\ref{eq7.3.9}\) por la ecuación\(\ref{eq7.3.11}\), rindiendo

\[\text{CMRR} = \dfrac{g_m (1 + \Delta ) r_{\mu}}{\Delta } \nonumber \]

Un enfoque similar se puede utilizar para calcular errores de modo común que surgen de otras fuentes, como la resistencia desigual de colector a emisor de transistor o valores desiguales de\(r_x\). Se puede demostrar que dado que cada uno de estos efectos es pequeño, hay poca interacción entre ellos, y es válido computar cada error por separado.

Como cuestión de interés práctico, es posible obtener transistores emparejados suficientemente bien para obtener valores de baja frecuencia para\(\text{CMRR}\) del orden de\(10^4\) a\(10^6\) con una simple conexión de amplificador diferencial.

Deriva atribuible a transistores bipolares

La razón del uso casi exclusivo del amplificador diferencial para los circuitos amplificadores d-c se debe a la cancelación de deriva inherente que ofrecen los componentes simétricos. El propósito de esta sección es indicar cómo se debe equilibrar el circuito para una deriva mínima.

Si un amplificador diferencial como el que se muestra en la Figura 7.4 se construye con componentes simétricos, el voltaje de salida diferencial\(v_{O1}\) es cero para\(v_{I1} = v_{I2}\). Si bien las resistencias están disponibles con características prácticamente coincidentes, la selección de transistores bien adaptados es un problema significativo.

Se ha supuesto hasta este punto que los transistores utilizados en un amplificador diferencial están emparejados en el sentido de que tienen corrientes de saturación iguales. Una medida del grado de coincidencia es especificar la relación de las corrientes de saturación para un par de transistores. Esta relación es exactamente la misma que la relación de las corrientes de colector de los dos transistores cuando se opera a tensiones iguales de base a emisor, ya que a una tensión de base a emisor\(V_{BE}\) (suponiendo operación a corrientes grandes en comparación con\(I_S\)), la corriente de colector de un transistor es

\[I_{C1} = I_{S1} e^{qV_{BE}/kT} \nonumber \]

mientras que el del segundo transistor es

\[I_{C2} = I_{S2} e^{qV_{BE}/kT} \nonumber \]

Alternativamente, el grado de coincidencia puede indicarse especificando la diferencia\(\Delta V\) entre los voltajes de base a emisor de los dos transistores cuando ambos funcionan con alguna corriente de colector\(I_C\). Esta especificación implica que en algún voltaje de base a emisor\(V_{BE}\)

\[I_{C1} = I_{S1} e^{qV_{BE}/kT} = I_C = I_{C2} = I_{S2} e^{q(V_{BE} + \Delta V)/kT}\label{eq7.3.15} \]

Esta medida de coincidencia se relaciona fácilmente con el grado de coincidencia entre las corrientes de saturación, ya que la ecuación\(\ref{eq7.3.15}\) muestra que

\[\dfrac{I_{S1}}{I_{S2}} = e^{q\Delta V/kT}\label{eq7.3.16} \]

La ecuación\(\ref{eq7.3.16}\) también muestra que el desajuste de voltaje de base a emisor\(\Delta V\),, es independiente del nivel de corriente de operación seleccionado para la prueba.

Si el circuito de la Figura 7.4 se utiliza como amplificador d-c, la cantidad\(\Delta V\) para el par de transistores es exactamente el desplazamiento referido a la entrada del amplificador, ya que esta tensión diferencial debe aplicarse a la entrada para igualar las corrientes del colector y así hacer\(v_{O1}\) cero. Por esta razón, los fabricantes de semiconductores normalmente especifican el grado de coincidencia entre dos transistores en términos de su diferencial de voltaje de base a emisor a corrientes iguales en lugar de como la relación de corrientes de saturación.

Varias opciones están disponibles para el diseñador para obtener pares bien emparejados para su uso en amplificadores diferenciales. Los transistores emparejados están disponibles en muchos fabricantes a un costo de 2 a 10 veces el de los dos dispositivos individuales. Estos transistores se montan frecuentemente en una sola lata de manera que se minimiza la temperatura diferencial de los dos chips. La mejor coincidencia especificada disponible en una serie particular de dispositivos es típicamente un diferencial de voltaje de base a emisor de 3 mV cuando los dispositivos operan a corrientes de colector iguales.

Una alternativa implica la coincidencia del usuario de los transistores. Esta posibilidad es atractiva por varias razones. Existen ventajas económicas, particularmente si se requieren grandes cantidades de pares emparejados, ya que bastan equipos relativamente modestos y ya que el esfuerzo requerido no es prohibitivo. Son posibles mejores coincidencias para un mayor número de parámetros que con los pares emparejados comprados. Sin embargo, la falta de dinero, paciencia y control ambiental (recuerde el coeficiente de temperatura típico de\(-2\ mV/ ^{\circ} C\)) generalmente limita las coincidencias de voltaje de base a emisor alcanzables al orden de\(0.5\ mV\). También es necesario proporcionar algún tipo de acoplamiento térmico para mantener los dispositivos emparejados a temperaturas iguales durante la operación.

Una tercera posibilidad es el uso de un par diferencial monolítico de circuito integrado. A través del control adecuado del procesamiento, todos los parámetros del transistor se emparejan simultáneamente, y con la tecnología actual son posibles tensiones diferenciales de base a emisor del orden de 1 mV. Se obtiene una excelente igualdad térmica por la proximidad de los dos dispositivos. Este enfoque se utiliza como parte integral de todos los amplificadores operativos monolíticos. También hay varios pares monolíticos emparejados individuales y múltiples disponibles para su uso en diseños discretos. Varios diseños monolíticos más sofisticados están disponibles (los ejemplos incluyen Fairchild Semiconductor\(\mu A726\) y\(\mu A727\)) que incluyen sensores de temperatura y elementos de calentamiento en el chip para mantener su temperatura relativamente constante. Los efectos de las variaciones de temperatura ambiente se eliminan en gran medida con esta técnica.

Figura 7.9 Equilibrio con potenciómetro emisor-circuito.

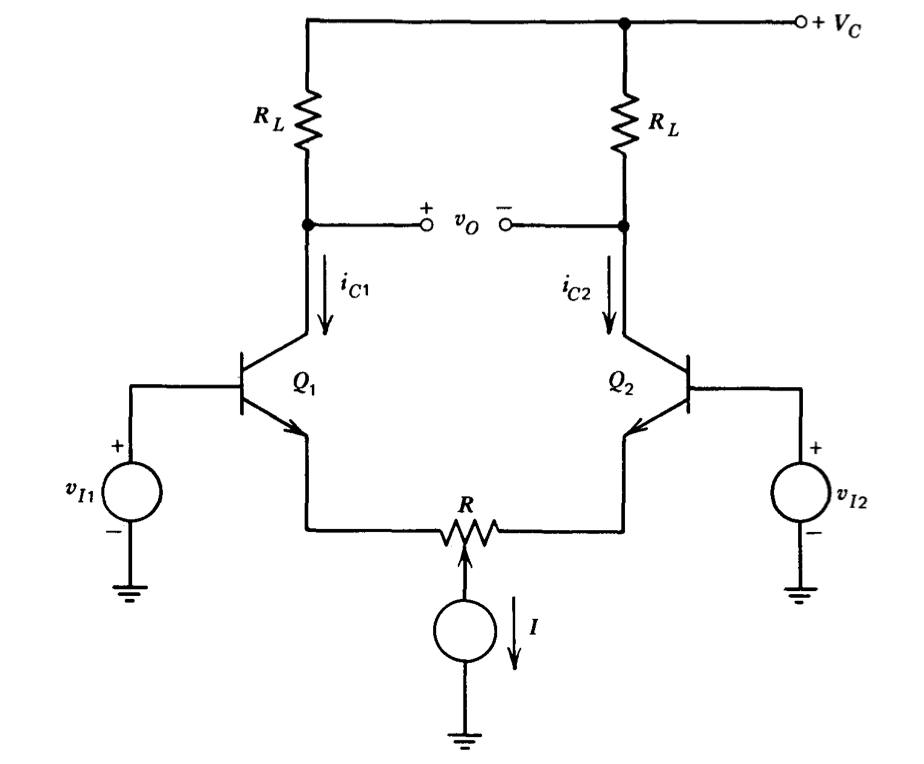
Independientemente del procedimiento de coincidencia utilizado, se requiere algún tipo de recorte para reducir el desplazamiento del amplificador a cero a una temperatura. Una técnica popular es incluir un potenciómetro en el circuito emisor como se muestra en la Figura 7.9. Las dos bases se cortocircuitan juntas y la olla se ajusta hasta que las dos corrientes colectoras sean iguales para que\(v_O = 0\). Este ajuste es posible para\(R > 2 \Delta V/I\), donde\(\Delta V\) está el diferencial de voltaje de base a emisor del par a corrientes de colector iguales. (El uso de un potenciómetro demasiado grande es indeseable ya que disminuye la transconductancia (La transconductancia de un par diferencial se define como la relación entre el cambio incremental en cualquiera de la corriente del colector y el voltaje de entrada diferencial incremental. Suponiendo que ambos transistores tienen valores grandes para\(\beta\) y una resistencia base despreciable, la transconductancia para la configuración mostrada en la Figura 7.9 es\(\left |\dfrac{i_{c1}}{v_{i1} - v_{i2}} \right | = \left |\dfrac{i_{c2}}{v_{i1} - v_{i2}} \right | \simeq \dfrac{1}{1/g_{m1} + 1/g_{m2} + R} \)) del par, y veremos que esta cantidad adquiere importancia cuando se considera el efecto de otros componentes del circuito sobre la deriva.) Si bien este método de equilibrio se usa frecuentemente, es fundamentalmente erróneo si el objetivo del diseño es minimizar la deriva con la temperatura. El enfoque ecualiza las corrientes del lector de col y por lo tanto asegura que un transistor opera a una tensión de base a emisor quiescente de\(v_{BE1}\), mientras que el otro opera a una tensión de\(v_{BE1} + \Delta V\). La diferencia requerida en voltajes de base a emisor se obtiene ajustando la olla para que las tensiones a través de sus dos segmentos difieran en\(\Delta V\). Dado que los voltajes a través de los segmentos de olla son los mismos siempre que se ajusta el voltaje de entrada para hacer vo cero (suponiendo que la ganancia de renta cur de base común de los transistores es uno, la corriente a través de cada segmento de olla debe ser\(I/2\) cuando\(v_O = 0\)), la deriva referida a la entrada con respecto a

la temperatura para este diseño es idéntica al cambio diferencial en los voltajes de base a emisor del transistor con la temperatura. De la Ecuación 7.2.5,

\[\dfrac{\partial}{\partial T} (v_{BE1} - v_{BE2})|_{i_{C1} = i_{C2} = \text{const}} = \left (\dfrac{v_{BE1} - V_{go}}{T} - \dfrac{3k}{q} \right ) - \left (\dfrac{v_{BE2} - V_{go}}{T} - \dfrac{3k}{q} \right ) = \dfrac{v_{BE1} - v{BE2}}{T} \nonumber \]

Dado que la diferencia\(v_{BE1} - v_{BE2}\) es\(\Delta V\),

\[\dfrac{\partial }{\partial T} (v_{BE1} - v_{BE2}) = \dfrac{\Delta V}{T} \nonumber \]

Por ejemplo, un\(3-mV\) desajuste a temperatura ambiente conduce a una deriva de\(10\ \mu V/ ^{\circ} C\).

Una alternativa es operar los transistores con tensiones iguales de base a emisor. Esta condición requiere que la relación colector-corriente de reposo sea igual a la relación de las corrientes de saturación del transistor, o

\[\dfrac{I_{C1}}{I_{C2}} = \dfrac{I_{S1}}{I_{S2}} = e^{q\Delta V/kT} \nonumber \]

Figura 7.10 Método para equilibrar con tensiones iguales de base a emisor.

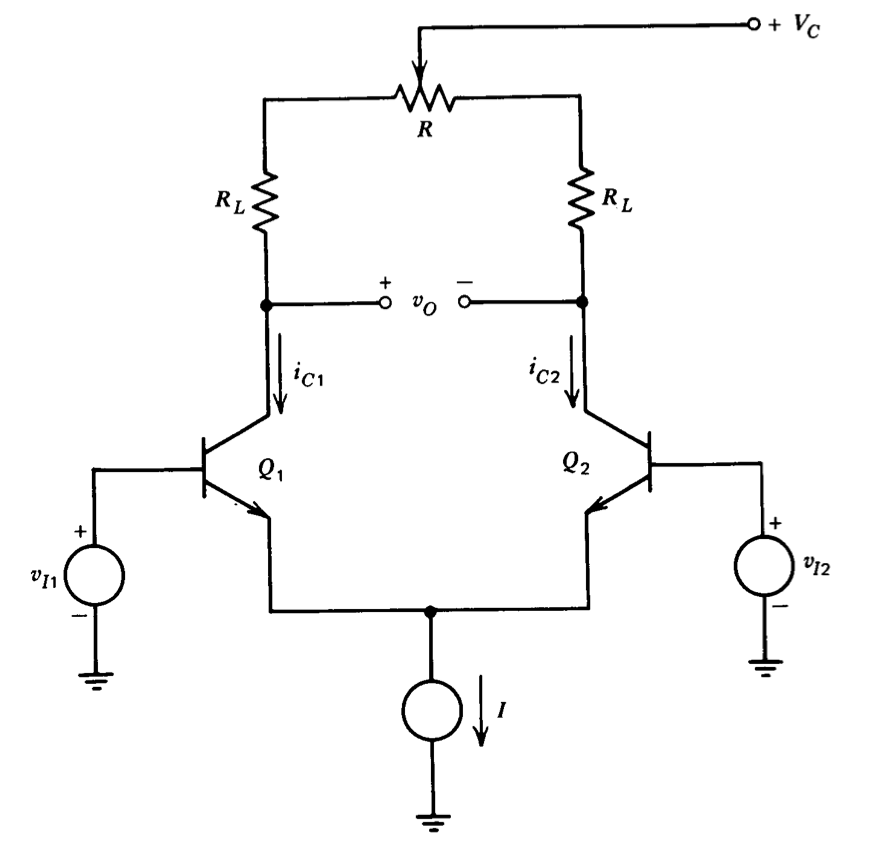
donde, como se definió anteriormente, (\ Delta V\) es la diferencia entre los voltajes de base a emisor de los dos dispositivos cuando son operados a corrientes de colector iguales. En este caso, un\(3-mV\) valor para\(\Delta V\) requiere una diferencia de 12% en las corrientes de colector para igualar los voltajes de base a emisor. Una posible configuración de circuito se muestra en la Figura 7.10. Las dos bases se cortocircuitan entre sí, lo que obliga a voltajes iguales de base a emisor y voltaje de entrada diferencial cero. Luego se ajusta el potenciómetro para hacer\(v_O = 0\). Los resultados de análisis anteriores indican que la deriva de temperatura atribuible a los transistores debe ser cero después de este ajuste. Si bien los valores muy bajos son alcanzables por este método, existen otros efectos detallados, descuidados en nuestro análisis simplificado, que conducen a una deriva distinta de cero. Es posible ajustar los voltajes relativos de base a emisor para compensar estos efectos. (A. H. Hoffait y R. D. Thornton, “Limitaciones de los amplificadores de CC de transistor”, Proceedings Institute of Electrical and Electronic Engineers, febrero de 1964.) En la práctica, incluso la técnica de equilibrado simplificada puede dar como resultado derivas de una fracción de microvoltio por grado centígrado.

Se destaca que esta técnica de equilibrado no debe considerarse un sustituto del emparejamiento cuidadoso de los dispositivos, sino más bien como un recorte final después del emparejamiento. Si un gran desajuste de voltaje de base a emisor se compensa con este método, hay una gran disipación de potencia diferencial con calentamiento diferencial asociado, las corrientes de base diferirán en gran cantidad y la transconductancia del par será significativamente menor que si se usan dispositivos bien emparejados. Por ejemplo, la compensación de una\(60-mV\) falta de coincidencia requiere corrientes de colector con una relación de 10 a 1 y disminuye la transconductancia en un factor de cinco en comparación con un par bien emparejado operado a la misma corriente total del emisor. El funcionamiento con corrientes de colector gravemente desequilibradas también desajusta todos los parámetros del transistor dependiente de la corriente.

Otras consideraciones sobre la deriva

Figura 7.11 Circuito con resistencias de carga desigual.

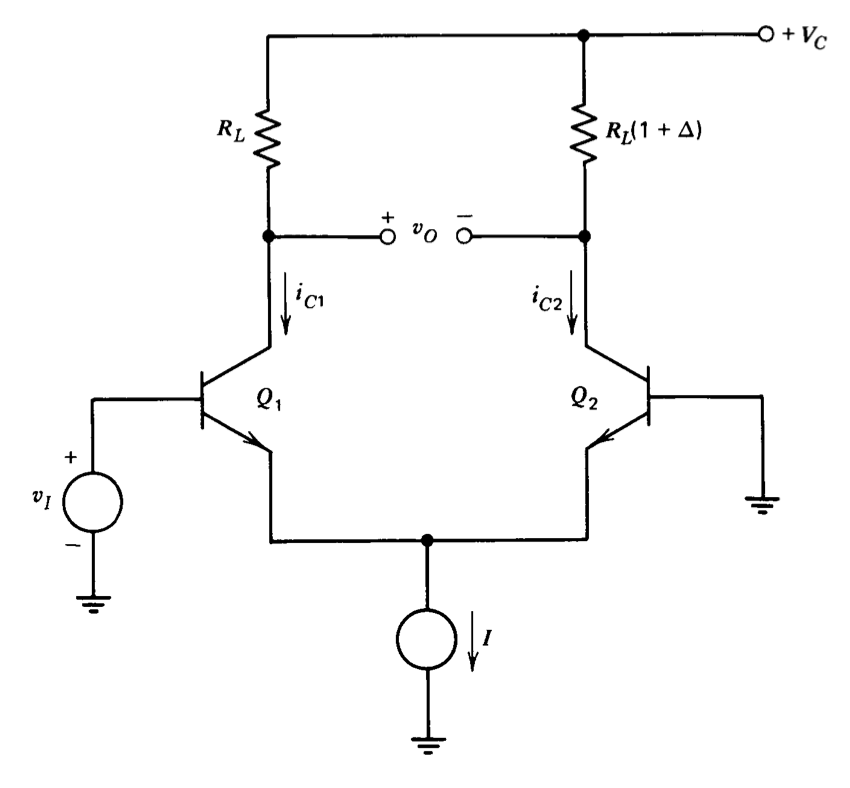
Es interesante observar que la excelente compensación que brinda incluso la técnica de equilibrado simplificada descrita anteriormente enfatiza la contribución de deriva de otros componentes en el circuito. Considera el circuito que se muestra en la Figura 7.11. (Por simplicidad se supone que las entradas se aplican a un solo lado del circuito). Supongamos que los transistores están perfectamente emparejados para que cuando las resistencias del colector sean iguales\(v_O = 0\) para\(v_I = 0\). Se produce una deriva si los valores relativos del colector-resistencia cambian como resultado de cambios diferenciales con la temperatura o el envejecimiento. La deriva atribuible a un desequilibrio fraccionario colector-resistencia se\(\Delta\) puede calcular de la siguiente manera. Con\(v_I = 0\),\(i_{C1} = i_{C2} \simeq I/2\). A medida\(v_i\) que se incrementa,\(i_{C1} = I/2 + (g_m/2)v_i\) y\(i_{C2} = 1/2 ­- (g_m/2)v_i\), donde\(g_m\) está la transconductancia de cualquiera de los dos transistores. (Se supone que\(r_{\pi} \gg r_x\) para los transistores.) Para volver\(v_O\) a cero, es necesario tener

\[\left ( \dfrac{I}{2} + \dfrac{g_m}{2} v_i \right ) R_L = \left ( \dfrac{I}{2} - \dfrac{g_m}{2} v_i \right ) (1 + \Delta ) R_L \nonumber \]

o

\[g_m v_i = \dfrac{\Delta I}{2} \nonumber \]

(Se\(g_mv_i \Delta R_L\) ha dejado caer un término que contiene el pequeño producto cruzado). Ya que cada dispositivo está operando a un nivel de corriente de reposo\(I/2\),\(g_m = qI/2kT \simeq 20I\) a temperatura ambiente. Por lo tanto, el voltaje de entrada requerido para devolver el voltaje de salida a cero (por definición la deriva referida a la entrada) es\(\Delta /40\). La importancia de esta sensibilidad se aprecia cuando se considera que dos resistencias ordinarias de composición de carbono de igual valor pueden tener coeficientes de temperatura que difieren tanto como una parte por mil por grado centígrado. El uso de tales resistencias resultaría en una deriva de amplificador de\(25 \mu V/ ^{\circ} C\)! Es claro que la calidad de las resistencias utilizadas es un factor importante cuando se diseña un\(1 \mu V/ ^{\circ} C\) amplificador.

Figura 7.12 Circuito equivalente para encontrar deriva en función de\(I_{CBO}\).

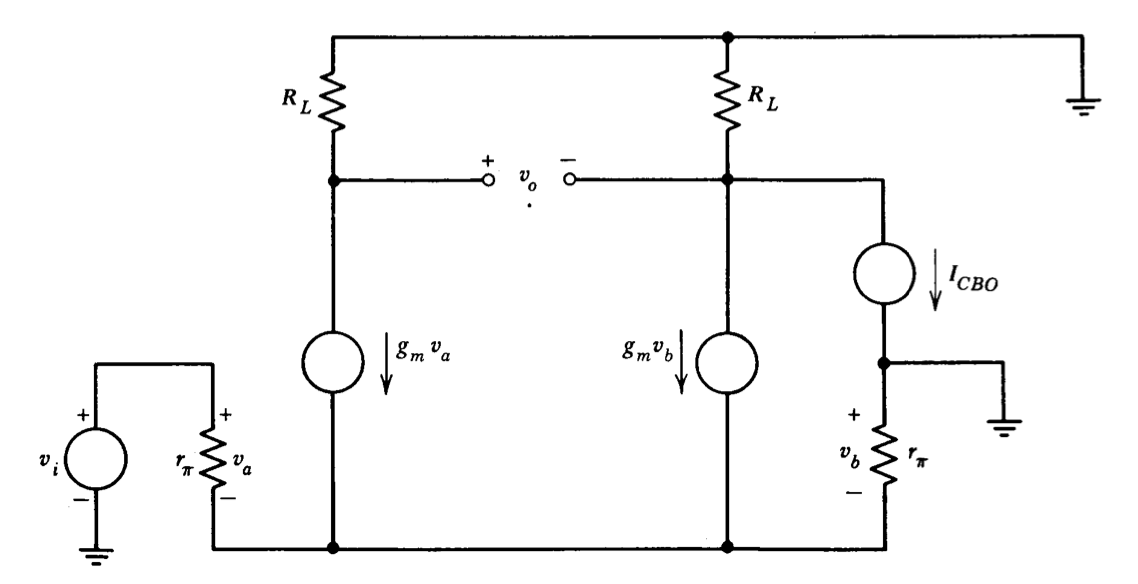
Se llega a una conclusión similar cuando se alcanzan los efectos de la corriente de fuga de colector a base\(I_{CBO}\) (Los supuestos a menudo utilizados para simplificar la física del dispositivo al contrario, esta cantidad no está relacionada con la corriente de saturación en la ecuación del transistor. La magnitud de Is está dominada por los efectos dentro del cuerpo del semiconductor, mientras que el componente dominante de\(I_{CBO}\), al menos a temperatura ambiente, resulta de efectos superficiales. Los coeficientes de temperatura son significativamente diferentes. Si bien\(I_S\) se consideran dobles cada uno\(6^{\circ} C\), la temperatura\(I_{CBO}\) cercana a la habitación normalmente se duplica cada\(10^{\circ} C\).). En la Figura 7.12 se muestra un circuito equivalente que\(I_{CBO}\) se puede utilizar para predecir la deriva de. Dado que la magnitud de\(I_{CBO}\) es probable que sea significativamente diferente para dos transistores de otro modo bien emparejados, solo se muestra un generador de corriente de fuga en la Figura 7.12. Su valor se puede hacer la diferencia entre las fugas si un componente no es despreciable. Procediendo como antes, el valor de\(v_i\) requerido para reducir la salida a cero se da resolviendo

\[\dfrac{g_m v_i}{2} = \dfrac{-g_m v_i}{2} + I_{CBO} \nonumber \]

para\(v_i\), cediendo

\[v_i = \dfrac{I_{CBO}}{g_m} \nonumber \]

La transconductancia de cualquiera de los transistores de entrada\(g_m\) puede estar relacionada con el nivel de polarización para el par diferencial (cada miembro opera a 1/2) como\(g_m = 20I\). Por lo tanto, el desplazamiento expresado en voltios es\(I_{CBO}/20I\). De nuevo se evocan valores típicos para ilustrar el problema. El FT107A (una opción atractiva para la etapa de entrada de un amplificador d-c ya que sus especificaciones incluyen un típico\(\beta\) de 1100 at\(10\mu A\) de corriente de colector!) tiene una corriente de fuga máxima especificada que aumenta de esencialmente cero\(25^{\circ} C\) a a\(1 \mu A\) at\(125^{\circ} C\). Por lo tanto, la deriva promedio resultante sobre el rango de\(100^{\circ} C\) temperatura para el dispositivo que opera a un nivel de corriente de colector de\(10 \mu A\) (\(I = 20 \mu A\)) está limitada por\(25 \mu V/^{\circ} C\). Afortunadamente el valor típico para\(I_{CBO}\) es 2% del valor máximo especificado, pero se requieren procedimientos de cribado adicionales para asegurar que este nivel inferior sea alcanzado por cualquier dispositivo en particular.

Vale la pena enfatizar la importancia del diseño térmico adecuado para los amplificadores d-c de baja deriva. Un diferencial de temperatura\(0.001^{\circ} C\) da como resultado un desplazamiento de\(2 \mu V\) para un par diferencial que se adapta perfectamente cuando las temperaturas de los transistores son idénticas. Varios factores influyen en el diferencial de temperatura de un par. Un buen contacto térmico entre los miembros de la pareja es obligatorio. Este contacto requerido se puede lograr ubicando los dos chips juntos en una placa térmicamente conductora, o mediante una construcción monolítica de circuito integrado.

También es necesario minimizar los efectos de calentamiento que perturban al par. El autocalentamiento como consecuencia de la potencia disipada en el par es particularmente importante. El autocalentamiento diferencial se reduce al operar los dos miembros del par a corrientes de colector bajas coincidentes y a baja tensión de colector. También se debe considerar la ubicación de otras fuentes de calor que puedan establecer gradientes térmicos a través del par. Estas fuentes se aíslan fácilmente en diseños de componentes discretos, pero imponen severas restricciones a la colocación de componentes en circuitos integrados.

Otro aspecto del problema térmico involucra la forma en que los transistores de amplificador diferencial se conectan a la señal de entrada o a otros componentes del circuito. Se forma un termopar con un\(20 \mu V/^{\circ} C\) coeficiente aproximado cuando el kovar, una aleación frecuentemente utilizada para conductores de transistores, se conecta al cobre. Por lo tanto, los gradientes térmicos a través del circuito, que dan como resultado diferentes temperaturas para las uniones de termopar conectadas en serie en la trayectoria de la señal, pueden contribuir a un voltaje de compensación significativo.