6.3: Teorema de superposición

Tan útil como la técnica de conversión de fuente demostró ser en el Ejemplo 6.2.3, no funcionará para todos los circuitos. Por lo tanto, se necesitan enfoques más generales. Uno de estos métodos es la superposición.

La superposición permite el análisis de circuitos multifuente serie-paralelo. La superposición solo se puede aplicar a redes que sean lineales y bilaterales. Además, no se puede utilizar para encontrar valores para funciones no lineales, como la potencia, directamente. Afortunadamente, si el circuito no contiene más que resistencias, y fuentes de voltaje ordinarias y fuentes de corriente, el circuito será una red bilateral lineal. Además, aunque la potencia es una función de ley cuadrada (es decir, es proporcional al cuadrado de voltaje o corriente), puede calcularse a partir de los valores de voltaje o corriente resultantes por lo que esto no presenta límites para el análisis.

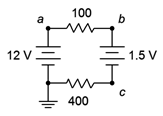
Figura 6.3.1 : Un circuito de doble fuente.

La idea básica es determinar la contribución de cada fuente por sí misma, y luego agregar los resultados para obtener la (s) respuesta (s) final (s). Empecemos con un ejemplo casi trivial para ilustrar la idea. Considere el circuito de la Figura 6.3.1 . Aquí tenemos dos fuentes de voltaje que accionan un par de resistencias. Se trata de un circuito básico en serie. La forma en que esto se abordó en el Capítulo 3 fue combinar las fuentes y las resistencias en una sola fuente y resistencia. La corriente circulante podría entonces ser encontrada usando la ley de Ohm. Como las dos fuentes están en oposición, el voltaje neto es de 10.5 voltios mientras que la resistencia total es de 500\(\Omega\). Esto produce una corriente circulante de 21 mA.

En lugar de este enfoque, consideremos la contribución de cada fuente por sí misma. Para ello, reemplazaremos todas las demás fuentes del circuito con su resistencia interna ideal. De trabajos anteriores hemos descubierto que la resistencia interna ideal de una fuente de voltaje es una corta, o cero ohmios. Así, terminamos con dos circuitos: uno con una fuente de 12 voltios que impulsa 100\(\Omega\), 400\(\Omega\) y un corto; y un segundo circuito con una fuente de 1.5 voltios que impulsa prácticamente lo mismo, pero con una dirección de corriente opuesta. El primer circuito produce una corriente en el sentido de las agujas del reloj de 12 V/ 500\(\Omega\), o 24 miliamperios. En tanto, el segundo circuito produce una corriente en sentido contrario a las agujas del reloj de 1.5 V/500\(\Omega\), o 3 mA. Como estas dos corrientes se oponen entre sí, la corriente resultante es 24 mA − 3 mA, o 21 mA, el mismo valor calculado originalmente. Por supuesto, este segundo método es menos eficiente que el método original pero ilustra el proceso. Más importante aún, este proceso se puede aplicar a una variedad de circuitos multifuente serie-paralelo. Un elemento clave es recordar las direcciones de las corrientes y polaridades de los voltajes creados en los subcircuitos. Sin estos datos, será imposible determinar si las diversas piezas del rompecabezas se suman o restan del total.

Para resumir la técnica de superposición:

• Para cada fuente de voltaje o corriente en el circuito original, cree un nuevo subcircuito. Los subcircuitos serán idénticos al original excepto que todas las fuentes distintas de la que se esté considerando serán reemplazadas por su resistencia interna ideal. Esto significa que todas las fuentes de voltaje restantes estarán cortocircuitadas y todas las fuentes de corriente restantes se abrirán.
• Etiquetar las direcciones de corriente y las polaridades de voltaje en cada uno de los nuevos subcircuitos, tal como lo genera la fuente bajo consideración.
• Resuelva cada uno de los subcircuitos para los voltajes y/o corrientes deseados utilizando técnicas estándar de análisis serie-paralelo. Asegúrese de anotar las polaridades de voltaje y las direcciones de corriente para estos elementos.
• Sumar todas las contribuciones de cada uno de los subcircuitos para llegar a los valores finales, asegurándose de tener en cuenta las direcciones de corriente y las polaridades de voltaje en el proceso.

Para poder manejar mejor la técnica de superposición, reexaminemos el circuito de doble fuente mostrado en la Figura 6.2.8 (repetido en la Figura 6.3.2 para facilitar la referencia). Esto lo resolveremos usando superposición. Como el circuito tiene dos fuentes, requerirá dos subcircuitos.

Ejemplo 6.3.1

Determine\(V_b\) para el circuito de la Figura 6.3.2 usando superposición.

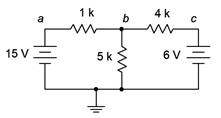
Figura 6.3.2 : Circuito por ejemplo 6.3.1 .

Como este circuito tiene dos fuentes de voltaje, se necesitarán dos subcircuitos. El primer subcircuito utilizará la fuente de 15 voltios. En consecuencia, la fuente de 6 voltios será reemplazada por su resistencia interna ideal, un corto. Este nuevo circuito se muestra en la Figura 6.3.3 .

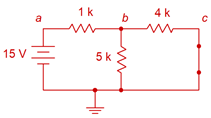
Figura 6.3.3 : Primer subcircuito para el circuito de la Figura 6.3.2 .

Las direcciones de corriente son las siguientes: la corriente sale de la fuente y viaja a través del 1 k\(\Omega\) produciendo una caída de voltaje + a − de izquierda a derecha. En\(b\) el nodo la corriente se divide. Los 4 k\(\Omega\) y 5 k\(\Omega\) están en paralelo por lo que ambos ven el mismo voltaje. Parte de la corriente fluye hacia abajo a través de la\(\Omega\) resistencia de 5 k produciendo una caída de voltaje + a − de arriba a abajo. El resto de la corriente fluye hacia la derecha, a través de los 4 k\(\Omega\), produciendo una caída de voltaje + a − de izquierda a derecha. \(V_b\)se puede determinar a través del divisor de voltaje entre el 1 k\(\Omega\) y el combo paralelo de los 5 k\(\Omega\) y 4 k\(\Omega\). 5 k\(\Omega\) en paralelo con 4 k\(\Omega\) es aproximadamente 2.222 k\(\Omega\).

\[V_b = E \frac{R_x}{R_x+R_y} \nonumber \]

\[V_b = 15V \frac{2.222 k \Omega}{2.222 k\Omega +1 k\Omega} \nonumber \]

\[V_b \approx 10.34 V \nonumber \]

El segundo subcircuito utilizará la fuente de 6 voltios. Por lo tanto, la fuente de 15 voltios será reemplazada por su resistencia interna ideal, un corto. Este nuevo circuito se muestra en la Figura 6.3.4 .

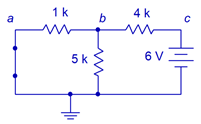
Figura 6.3.4 : Segundo subcircuito para el circuito de la Figura 6.3.2 .

Las direcciones de corriente son las siguientes: la corriente sale de la fuente y viaja a través de los 4 k\(\Omega\) produciendo una caída de voltaje + a − de derecha a izquierda. En\(b\) el nodo la corriente se divide. Ahora los 1 k\(\Omega\) y 5 k\(\Omega\) están en paralelo por lo que ambos ven el mismo voltaje. Parte de la corriente fluye hacia abajo a través de la\(\Omega\) resistencia de 5 k produciendo una caída de voltaje + a − de arriba a abajo, tal como lo hizo en el primer subcircuito. El resto de la corriente fluye hacia la izquierda, a través del 1 k\(\Omega\), produciendo una caída de voltaje + a − de derecha a izquierda. Una vez más, se\(V_b\) puede determinar vía divisor de voltaje, esta vez entre el 4 k\(\Omega\) y el combo paralelo de los 5 k\(\Omega\) y 1 k\(\Omega\) es aproximadamente 833.3\(\Omega\).

\[V_b = E \frac{R_x}{R_x+R_y} \nonumber \]

\[V_b = 6V \frac{833.3\Omega}{833.3\Omega +4 k\Omega} \nonumber \]

\[V_b \approx 1.034 V \nonumber \]

Ambos subcircuitos muestran polaridades de + a − de arriba a abajo para\(V_b\), por lo tanto estos dos voltajes simplemente se suman, para un total de aproximadamente 11.37 voltios. Esto concuerda muy bien con el resultado obtenido mediante conversiones de origen. La ligera desviación en el dígito final se debe sin duda al redondeo de valores intermedios, como las combinaciones de resistencias.

Es instructivo seguir este ejemplo más e investigar una corriente. En la versión de conversión de fuente se descubrió que la corriente a través de la\(\Omega\) resistencia de 1 k es de 3.62 mA y fluye de izquierda a derecha. Usando superposición, la corriente correspondiente en el primer subcircuito se puede encontrar usando KVL y la ley de Ohm, (15 V − 10.34 V)/1 k\(\Omega\), o 4.66 mA fluyendo de izquierda a derecha. En el segundo subcircuito, esta corriente se puede obtener usando solo la ley de Ohm, 1.034 V/1 k\(\Omega\), o 1.034 mA fluyendo de derecha a izquierda. Como esta corriente se opone a la corriente del primer subcircuito, los dos valores están restando dejando aproximadamente 3.63 mA fluyendo de izquierda a derecha, coincidiendo con la respuesta original dentro del error de redondeo.

Simulación por Computadora

Para una mayor verificación, el circuito del Ejemplo 6.3.1 se introduce en un simulador como se muestra en la Figura 6.3.5 .

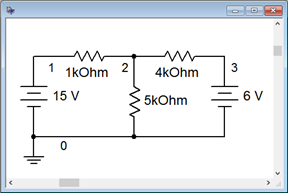
Figura 6.3.5 : El circuito de Ejemplo 6.3.1 en un simulador.

Se realiza un análisis de punto de funcionamiento de CC, como se muestra en la Figura 6.3.6 .

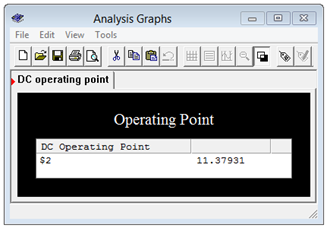
Figura 6.3.6 : Resultados de simulación para el circuito de Ejemplo 6.3.1 .

El voltaje en el nodo 2, que está\(V_b\) en el circuito original, concuerda muy bien con los valores calculados previamente.

Esta exploración muestra que la técnica de superposición ofrece un método bastante sencillo para resolver una variedad de circuitos multifuente serie-paralelo. Sin embargo, no está exento de limitaciones. Primero, si un circuito tiene un gran número de fuentes, la superposición puede llegar a ser un poco tediosa ya que requiere tantos subcircuitos como fuentes haya, y cada uno de estos subcircuitos requiere soluciones separadas. En segundo lugar, hay algunas configuraciones serie-paralelo que la superposición junto con las técnicas de análisis serieparalelo no resolverá. Investigaremos los métodos para tratar estos temas más adelante en este capítulo y en el siguiente capítulo.