6.6: Teorema de transferencia de potencia máxima

Dada una fuente de voltaje simple con resistencia interna, una pregunta útil es “¿Qué valor de resistencia de carga producirá la cantidad máxima de potencia en la carga?” Si bien no es cierto que maximizar la potencia de carga sea un objetivo de todos los diseños de circuitos, es un objetivo de una parte de ellos y por lo tanto merece una mirada más cercana. Considere el circuito básico representado en la Figura 6.6.1 con fuente\(E\), resistencia interna de fuente\(R_i\) y resistencia a la carga\(R\).

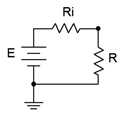
Figura 6.6.1 : Definición de la transferencia máxima de potencia.

Nos gustaría describir la potencia de carga en términos de la resistencia de carga. Para facilitar el trabajo, podemos normalizar la fuente de voltaje\(E\) a 1 voltio y la resistencia de la fuente\(R_i\) a 1 Ohm. Al hacer esto,\(R\) también se convierte en un valor normalizado, es decir, ya no representa un valor de resistencia simple sino que representa una relación en comparación con\(R_i\). De esta manera el análisis funcionará para cualquier conjunto de valores fuente. Tenga en cuenta que el valor de\(E\) escalará igualmente la potencia en ambos\(R_i\) y\(R\), por lo que no se necesita un valor preciso, y por lo tanto, también podemos elegir 1 voltio por conveniencia.

La potencia en la carga se puede determinar usando\(I^2 R\) donde\(I = E / (R_i+R)\). Usando nuestros valores normalizados\(I = 1 / (1+R)\) y por lo tanto la potencia de carga es:

\[P = \left( \frac{1}{1+R} \right)^2 R \text{ or after expanding, } P = \frac{R}{R^2+2 R+1} \nonumber \]

Ahora tenemos una ecuación que describe la potencia de carga en términos de la resistencia de carga. Antes de ir más lejos, echa un vistazo a lo que te dice esta ecuación, en general. Es obvio que la potencia máxima no ocurrirá en los extremos. Si\(R = 0\) o\(R = \infty \) (es decir, carga en cortocircuito o abierta) la potencia de carga es cero. Si bien el cortocircuito de la carga producirá la corriente de carga máxima, también producirá voltaje de carga cero y, por lo tanto, no tendrá energía. Del mismo modo, al abrir la carga se producirá un voltaje máximo de carga, pero también producirá corriente de carga cero, y nuevamente, potencia sin carga. Para encontrar el valor preciso que produce la máxima potencia de carga, la prueba se puede dividir en dos porciones principales. El primero implica graficar la función y el segundo requiere cálculo diferencial para resolver un valor preciso. Procederemos con la porción gráfica que nos llevará a la respuesta. La prueba más rigurosa del segundo método se detalla en el Apéndice C.

Graficando la función de potencia\(P = R / (R^2+2R+1)\)

Esto se puede hacer por partes, mirando la contribución de cada término, y luego combinándolo para formar el resultado final. Primero, considere el denominador\(R^2 + 2R + 1\). Consta de tres segmentos. El más simple es la línea horizontal en +1. El\(2R\) término crea una línea recta con pendiente 2 comenzando en el origen. El\(R^2\) término crea una curva simple con pendiente creciente que comienza en el origen, cruza la línea horizontal +1 en\(R = 1\) y también cruza la\(2R\) línea en\(R = 2\). Estos elementos se dibujan individualmente y luego se suman como se ilustra en la Figura 6.6.2 .

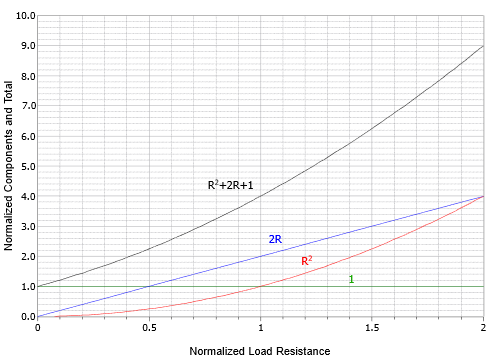
Figura 6.6.2 : Los tres términos de la ecuación de potencia se trazaron individualmente y luego se sumaron.

Por supuesto, debemos recordar que realmente queremos\(1 / ( R^2 + 2R + 1)\) y así trazamos el recíproco del combo como se muestra en la Figura 6.6.3 (curva roja). También incluimos el término numerador,\(R\). Esto se muestra como una línea recta (azul) con una pendiente de 1. Finalmente, estas dos curvas se multiplican juntas para producir la ecuación de potencia de carga (negro).

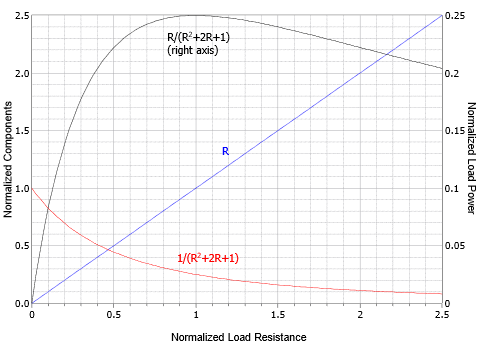
Figura 6.6.3 : La ecuación de potencia y los componentes trazados.

Un examen minucioso de la curva de potencia mostrará que el pico se produce en\(R = 1\). Esto es más fácil de ver si trazamos la curva de potencia completada usando un eje horizontal logarítmico y también escalamos el eje vertical al 100%, como se muestra en la Figura 6.6.4 . El pico es más aparente y la curva es simétrica en forma más que asimétrica. Esto refuerza la idea de que la proporción de las resistencias es lo que importa.

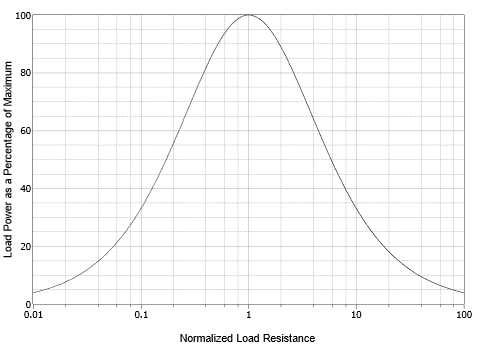
Figura 6.6.4 : La curva de potencia de carga con eje logarítmico mostrando simetría.

Por último, podemos afirmar:

\[\text{Maximum load power will be achieved when the load resistance is equal to the internal resistance of the driving source.} \nonumber \]

Ningún otro valor de resistencia de carga producirá una mayor potencia de carga. Para el circuito de la Figura 6.6.1 , esto significa que\(R\) debe ser igual\(R_i\). Como ejercicio, podemos intentar sustituir algunos valores alrededor del pico para verificar esto. Por ejemplo, dado\(E\) = 1 V y\(R_i\) = 1\(\Omega\), calculamos\(P\) para\(R\) = 0.5\(\Omega\)\(\Omega\), 1 y 2\(\Omega\):

\[P_{0.5} = 0.5/(0.5^2+2 \cdot 0.5+1) = 2/9 \nonumber \]

\[P_1 = 1/(1^2+2 \cdot 1+1) = 2/8 = 1/4 \nonumber \]

\[P_2 = 2/(2^2+2 \cdot 2+1) = 2/9 \nonumber \]

También puedes probar esto con variaciones extremadamente pequeñas como\(R\) = 0.9999\(\Omega\) junto con\(R\) = 1.0001\(\Omega\) y no lograrás un valor igual o superior a 1/4 Watt.

Si bien la coincidencia de la resistencia produce la potencia de carga máxima, no produce corriente de carga máxima o voltaje de carga máxima. De hecho, esta condición produce un voltaje de carga y una corriente de carga que son la mitad de sus máximos. Su producto, sin embargo, está al máximo. Además, la eficiencia a la potencia de carga máxima es solo del 50% (es decir, solo la mitad de toda la energía generada va a la carga y la otra mitad se desperdicia internamente). Valores\(R\) mayores que\(R_i\) lograrán mayor eficiencia pero con una potencia de carga reducida. A veces favorecemos la eficiencia sobre la potencia de carga máxima.

Como cualquier red lineal de dos puntos puede reducirse a algo así como Figura 6.6.1 usando el teorema de Thévenin, combinar los dos teoremas nos permite determinar las condiciones de potencia máxima para cualquier resistencia en un circuito complejo.