11.7: Problemas

11.1. En los ejemplos siguientes, identifique si\(f\) es una función o una funcional.

• Una parábola es descrita por\(f(x) = x^2\).
• Dadas dos formas de energía y un camino\(y(t)\),\(f\) es el lagrangiano del sistema\(\mathcal{L} \left( t, y, \frac{dy}{dt} \right)\).
• Dada la magnitud de la velocidad\(|\overrightarrow{v}(t)|\) de un objeto,\(f\) representa la distancia que recorre el objeto del tiempo 0 al tiempo 3600 segundos.
• Dada la posición\((x, y, z)\) en el espacio,\(f(x, y, z)\) representa la distancia desde ese punto hasta el origen.

11.2. Un sistema tiene el lagrangiano\(\mathcal{L} \left( t, y, \frac{dy}{dt} \right) = \left(\frac{dy}{dt}\right)^3 + e^{3y}\). Encuentra una ecuación para el camino\(y(t)\) que minimice la acción\(\int_{t_{1}}^{t_{2}} \mathcal{L}\left(t, y, \frac{d y}{d t}\right) d t\). (El resultado es no lineal, así que no intentes resolverlo.)

11.3. Un sistema tiene lagrangiano\(\mathcal{L} \left( t, y, \frac{dy}{dt} \right) = \frac{1}{2}\left(\frac{dy}{dt}\right)^2 + \frac{1}{2} \cdot y^{-2}\). Encuentra la ecuación de movimiento correspondiente. (El resultado es no lineal, así que no intentes resolverlo.)

11.4. La Figura 11.4.2 ilustra tres posibles trayectorias para el sistema de resorte de masa y sus acciones correspondientes. Los caminos considerados son:

\[x_{1}(t) = 2 t-1\nonumber \]

\[x_{2}(t) = 2 t^2-1\nonumber \]

\[x_{3}(t) =-\cos (\pi t)\nonumber \]

Para cada ruta, calcule la acción usando la Ecuación 11.4.10 para verificar los valores mostrados en la figura. Asumir una masa de\(m\) =1 kg y una constante de resorte de\(K = \pi^2 \frac{J}{m^2}\).

11.5. La figura muestra un resorte de torsión. Puede almacenar energía\(\frac{1}{2} \mathbb{K} \theta^{2}\) potencial y puede convertir energía potencial en energía cinética\(\frac{1}{2} \mathbb{I}\left(\frac{d \theta}{d t}\right)^{2}\). En estas expresiones,\(\theta(t)\) es la magnitud del ángulo que el resorte gira en radianes, y\(\omega=\frac{d \theta}{d t}\) es la magnitud de la velocidad angular en radianes por segundo. \(\mathbb{K}\)es la constante del resorte de torsión, y\(I\) es el momento (constante) de inercia.

(a) Encontrar el lagrangiano.

(b) Utilice la ecuación de Euler-Lagrange para encontrar una ecuación diferencial que describa\(\theta(t)\).

(c) Demostrar que la energía se conserva en este sistema demostrando que\(\frac{dH}{dt} = 0\).

d) Establecer las ecuaciones de Hamilton.

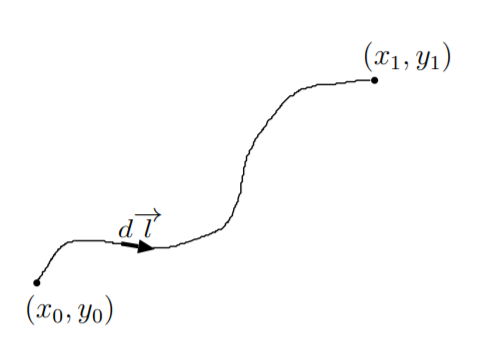
11.6. El propósito de este problema es derivar el camino más corto\(y(x)\) entre los puntos\((x_0, y_0)\) y\((x_1, y_1)\). Considera un camino arbitrario entre estos puntos como se muestra en la figura. Podemos romper el camino en elementos diferenciales\(d\overrightarrow{l}=d x \hat{a}_{x}+d y \hat{a}_{y}\). La magnitud de cada elemento diferencial es

\[|d \overrightarrow{l}|=\sqrt{(d x)^{2}+(d y)^{2}}=d x \sqrt{1+\left(\frac{d y}{d x}\right)^{2}}.\nonumber \]

La distancia entre los puntos puede ser descrita por la acción

\[\mathbb{S}=\int_{x_{0}}^{x_{1}} \sqrt{1+\left(\frac{d y}{d x}\right)^{2}} d x.\nonumber \]

Para encontrar el camino\(y(x)\) que minimiza la acción, podemos resolver la ecuación de Euler-Lagrange, con\(\mathcal{L}=\sqrt{1+\left(\frac{d y}{d x}\right)^{2}}\) como la lagrangiana, para este camino más corto\(y(x)\). Este enfoque se puede utilizar porque queremos minimizar la integral de algunos funcionales\(\mathcal{L}\) aunque este funcional no representa una diferencia de energía [163, p. 33].

Configurar la ecuación de Euler-Lagrange, y resolverlo para el camino más corto,\(y(x)\).

Pista 1: La respuesta a este problema es que el camino más corto entre dos puntos es una línea recta. Aquí, derivarás este resultado.

Pista 2: En los ejemplos de este capítulo, el lagrangiano tenía la forma\(\mathcal{L} \left( t, y, \frac{dy}{dt} \right)\) con variable\(t\) y trayectoria independientes\(y(t)\). Aquí, el lagrangiano tiene la forma\(\mathcal{L} \left( x, y, \frac{dy}{dx} \right)\) donde la variable independiente es posición\(x\), y el camino es\(y(x)\).

Pista 3: Si\(\frac{d} {dx} (something) = 0\), entonces sabes que\((something)\) es constante.

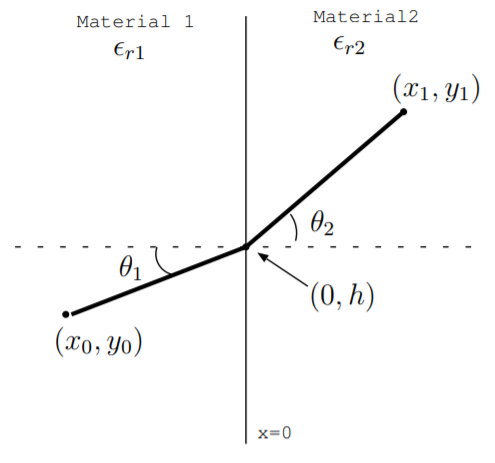
11.7. La luz viaja a lo largo del camino más rápido entre dos puntos. A esta idea se le conoce como principio de Fermat. En un material con permitividad\(\epsilon_r\) y permeabilidad relativas\(\mu_0\), la luz viaja a la velocidad constante\(\frac{c}{\sqrt{\epsilon_{r}}}\) donde\(c\) está la velocidad de la luz en el espacio libre. En Prob. 11.6, mostramos que el camino más corto entre dos puntos es una línea recta, por lo que en un material uniforme, la luz viajará a lo largo de una línea recta entre dos puntos. Sin embargo, ¿y si la luz viaja a través de una unión entre dos materiales? En este problema, vamos a responder a esta pregunta y derivar un famoso resultado conocido como ley de Snell.

Considera la figura a continuación. Supongamos que un rayo de luz viaja de\((x_0, y_0)\) a\((x_1, y_1)\) lo largo del camino que toma el menor tiempo. El material 1 tiene permitividad relativa\(\epsilon_{r1}\), por lo que la luz viaja en ese material a una velocidad constante\(\frac{c}{\sqrt{\epsilon_{r1}}}\). El material 2 tiene permitividad relativa\(\epsilon_{r2}\), por lo que la luz viaja en ese material a una velocidad constante\(\frac{c}{\sqrt{\epsilon_{r2}}}\). Como derivamos en el Prob. 11.6, la luz viaja a lo largo de una línea recta en el material 1, y viaja a lo largo de una línea recta en el material 2. Sin embargo, las líneas tienen diferentes pendientes como se muestra en la figura. Supongamos que la unión de los dos materiales ocurre en\(x = 0\).

(a) Encontrar una ecuación para el tiempo total que tarda la luz en viajar en función de\(h\), la distancia vertical a la que la trayectoria cruza el\(y\) eje. Tenga en cuenta que aquí está encontrando una función\(F(h)\), no una funcional. Puedes usar el hecho de que sabes que la luz sigue una línea recta dentro de cada material para encontrar esta función.

(b) El camino seguido por la luz toma el tiempo mínimo, por lo que la derivada\(\frac{dF}{dh} = 0\). Usa esta idea para encontrar una ecuación para la altura vertical desconocida\(h\). Su respuesta se puede escribir en función de las constantes conocidas\(\epsilon_{r1}\),\(\epsilon_{r2}\),\(x_0\),\(y_0\)\(x_1\),\(y_1\), y\(c\). No es necesario resolver por\(h\) aquí, sino que solo evalúa la derivada y ponla a cero.

(c) Usa tu resultado en la parte b anterior para derivar la ley de Snell:

\[\sqrt{\epsilon_{r 1}} \sin \theta_{1}=\sqrt{\epsilon_{r 2}} \sin \theta_{2}.\nonumber \]

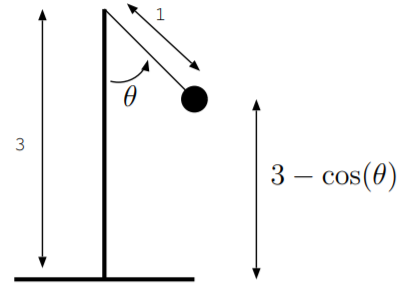
11.8. Un péndulo convierte la energía cinética hacia y desde la energía potencial gravitacional. Como se muestra en la figura, una bola de masa m es colgada por una cuerda de 1 m de largo. El péndulo está montado sobre una base que tiene 3 m de altura. Como se muestra en la figura,\(\theta(t)\) es el ángulo del péndulo. La energía cinética de la bola viene dada por\(E_{kinetic} = \frac{1}{2}m \left(\frac{d\theta}{dt}\right)^2\), y la energía potencial gravitacional viene dada por\(E_{p.e.} = mg (3 − \cos \theta)\). La cantidad\(g\) es la constante gravitacional,\(g = 9.8 \frac{m}{s^2}\).

(a) Encontrar\(\mathcal{L}\), el lagrangiano del sistema.

b) Encontrar\(H\), el hamiltoniano del sistema.

(c) Establecer la ecuación de Euler-Lagrange, y utilizarla para encontrar la ecuación de movimiento para\(\theta(t)\), el ángulo del péndulo en función del tiempo.

(d) Demostrar que la energía se conserva en este sistema demostrando que\(\frac{dH}{dt} = 0\).

La ecuación de movimiento que se encuentra en la parte c es no lineal, así que no intentes resolverla. Curiosamente, sí tiene una solución de forma cerrada [164, Ch. 6]. (Este problema es una versión modificada de un ejemplo en referencia [163].)

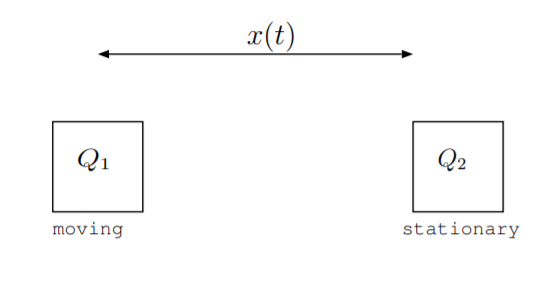
11.9. Como se muestra en la figura, un objeto de carga\(Q_1\) y masa\(m\) se mueve cerca de un objeto estacionario con carga\(Q_2\). Supongamos que la masa y las cargas son constantes, y asume que los objetos están rodeados de espacio libre. La energía cinética del objeto en movimiento se convierte a o a partir de la energía almacenada en el campo eléctrico entre los objetos. La energía cinética del objeto en movimiento viene dada por\(\frac{1}{2}m\left(\frac{dx}{dt}\right)^2\). La energía del campo eléctrico viene dada por\(\frac{Q_1Q_2}{4\pi\epsilon_0x}\) donde\(\epsilon_0\) está la permitividad del espacio libre. La distancia entre los objetos viene dada por\(x(t)\).

(a) Encontrar el lagrangiano del sistema.

b) Encontrar el impulso generalizado.

c) Encontrar el potencial generalizado.

d) Encontrar la ecuación de movimiento para la trayectoria\(x(t)\) del sistema. (No trates de resolver esta ecuación no lineal.)

e) Encontrar la energía total del sistema.

(f) Demostrar que la energía se conserva en este sistema.