11.5: Ejercicios
- Page ID
- 87250
Considere una aeronave que vuela a altitud constante\(h\) como se ilustra en la Figura 11.21. Supongamos que la Tierra está rotando a velocidad angular\(\vec{\Omega}_E = \Omega \cdot \vec{k}_E\), y no hay viento (condiciones de calma). Supongamos también que la aeronave está equipada con un sistema de navegación inercial con correa hacia abajo. En el momento\(t\), los acelerómetros y giroscopios están proporcionando las siguientes medidas:
- Velocidad angular:\(\vec{W} = W_x \cdot \vec{i}_b + W_y \cdot \vec{j}_b + W_z \cdot \vec{k}_b \approx 0\).
- Aceleraciones Cuerpo-Marco: 18\(\vec{a}_b = a_x \cdot \vec{i}_b + a_y \cdot \vec{j}_b + a_z \cdot \vec{k}_b\).
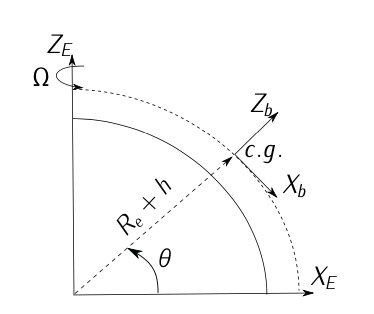
Figura 11.19: Sistema de navegación inercial (Ejercicio 3.1)
Considerar:
- la aeronave está volando a velocidad\(\vec{V} = V \cdot \vec{i}_b\) en el momento\(t\).
- el ángulo\(\theta\) puede considerarse aproximadamente constante.
Obtener:
- una expresión simbólica de los términos de aceleración\(a_x\)\(a_z\),\(a_y\) y, identificando aquellos que se deben al movimiento de la aeronave con respecto a la Tierra y aquellos que se deben a efectos inerciales y gravitacionales.
- Sustituir usando los valores a continuación y proporcionar el valor (y dirección) de la aceleración de la aeronave con respecto a la Tierra:
\(\bullet\)\(\Omega = 1\ rev./day\).
\(\bullet\)\(W_x \approx 0; W_y \approx 0\)
\(\bullet\)\(a_x = 0.9831\ m/s^2; a_y = 0.0257\ m/s^2, a_z = -9.8269\ m/s^2\).
\(\bullet\)\(V = 250\ m/s; h = 11.000\ m\).
\(\bullet\)\(R_E = 6378\ km; g = 9.81\ m/s^2\).
\(\bullet\)\(\theta = 45\ deg\).
- Contestar
-
Comencemos diciendo que la aceleración absoluta de un cuerpo es\(\vec{a}_i = \tfrac{d^2 \vec{r}}{dt^2}|_i\), y la velocidad de un cuerpo es\(\vec{V}_i = \tfrac{d\vec{r}}{dt}|_i\), siendo encuadrar\(i\) un marco de referencia inercial (por ejemplo, una estrella fija) y\(\vec{r}\) el vector de radio y\(t\) el tiempo.
Entonces, según la segunda ley de Newton:\(m \cdot \tfrac{d^2 \vec{r}}{dt^2}|_i = \sum \vec{F}_{ext}\), siendo\(m\) la masa del cuerpo y\(F_{ext}\) las fuerzas externas.
Usando la fórmula de Coriolis, se tiene que la derivada sobre una magnitud vectorial genérica (\(\vec{A}\)) en términos absolutos (con respecto a un marco de referencia inercial\(i\)) es igual a su derivada en términos relativos (con respecto a un marco de referencia no inercial\(e\)) más el producto vectorial del velocidad angular relativa de los dos marcos (\(\vec{w}_{ei}\)) y la magnitud vectorial genérica\(\vec{A}\). En palabras de orden:
\[\dfrac{d\vec{A}}{dt}|_i = \dfrac{d\vec{A}}{dt}|_e + \vec{w}_{ei} \wedge \vec{A}\label{eq11.5.1}\]
Así, podemos decir que:
\[\dfrac{d\vec{r}}{dt}|_i = \dfrac{d\vec{r}}{dt}|_e + \vec{w}_{ei} \wedge \vec{r}\]
Tomando derivados:
\[\dfrac{d^2\vec{r}}{dt^2}|_i = \dfrac{d^2\vec{r}}{dt^2}|_e + \dfrac{d}{dt}[\vec{w}_{ei} \wedge \vec{r}]\]
Esto da como resultado:
\[\dfrac{d\vec{V}}{dt}|_i = \dfrac{d\vec{V}}{dt}|_e + \vec{w}_{ei} \wedge \vec{V}\label{eq11.5.4}\]
En otras palabras, los términos absolutos son iguales a los términos relativos más los términos de Coriolis. También podemos decir que:
\[\dfrac{d^2\vec{r}}{dt^2}|_i = \dfrac{d}{dt} (\dfrac{d\vec{r}}{dt}|_i)|_i = \dfrac{d}{dt} (V + \vec{w}_{ei} \wedge \vec{r})|_i,\]
que elaborando rendimientos:
\[\dfrac{d^2\vec{r}}{dt^2}|_i = \dfrac{d\vec{V}}{dt}|_i + \dfrac{d}{dt}(\vec{w}_{ei} \wedge \vec{r})|_i\label{eq11.5.6}\]
La ecuación (\(\ref{eq11.5.6}\)) también se conoce como ecuación de navegación. Podemos aplicar la fórmula de Coriolis en (\(\ref{eq11.5.1}\)) al primer término del lado derecho en la Ecuación (\(\ref{eq11.5.6}\)), que rinde\(\tfrac{d\vec{V}}{dt}|_e + \vec{w}_{ei} \wedge \vec{V}|_e\) como en la Eq. (\(\ref{eq11.5.4}\)), y al segundo término del lado derecho en la Ecuación (\(\ref{eq11.5.6}\)), que rinde\(\tfrac{d(\vec{w}_{ei} \wedge \vec{r})}{dt} + \vec{w}_{ei} \wedge (\vec{w}_{ei} \wedge \vec{r})\). Así, la Ec. (\(\ref{eq11.5.6}\)) resultados en:
\[\vec{a} |_i = \vec{a}|_e + 2 \cdot \vec{w}_{ei} \wedge \vec{V} + \vec{w}_{ei} \wedge (\vec{w}_{ei} \wedge \vec{r}),\label{eq11.5.7}\]
donde\(\vec{V}\) y\(\vec{r}\) son magnitudes referidas al marco de referencia no inercial\(e\).
La ecuación (\(\ref{eq11.5.7}\)) es la composición bien conocida de la ecuación de aceleraciones. En el contexto de la navegación, establece que la aceleración absoluta (con respecto a un marco de referencia inercial i) es igual a la aceleración relativa (con respecto a un marco de referencia no inercial e, típicamente la Tierra) más efectos Coriolis (segundo término en el lado derecho de (\(\ref{eq11.5.7}\))) y efectos centrífugos (tercer término en el lado derecho de (\(\ref{eq11.5.7}\))).
En el contexto del problema analizado, las aceleraciones medidas por la Unidad de Medición Inercial son absolutas (\(\vec{a}_b\)), incluyendo efectos gravitacionales y términos inerciales (Coriolis y centrífugos). Sin embargo, para poder calcular aún más la posición de la aeronave con respecto a la Tierra (\(vec{a}_e\)), nos interesa la aceleración relativa, es decir, la aceleración del cuerpo (la aeronave) con respecto a la Tierra. En otras palabras:
\[\vec{a}_b = \vec{a}_e + \vec{g} + Coriolis + Centrifugal\]
Trabajemos ahora en cada uno de estos términos. Primero, defina los siguientes vectores:
\[\vec{g} = -g \cdot \vec{k}_b\]
\[\vec{w}_{ei} = \Omega \cdot \vec{k}_e\]
\[\vec{r} = (R_e + h) \cdot \vec{k}_b\]
\[\vec{V} = V \cdot \vec{i}_b\]
Entonces, operando, uno tiene:
\[Coriolis: 2 \Omega V \sin \theta \cdot \vec{j}_b\]
\[Centrifugal: -\Omega^2 (R_e + h) \cos \theta \cdot \vec{i}_e\]
\[Gravity: -g \cdot \vec{k}_b.\]
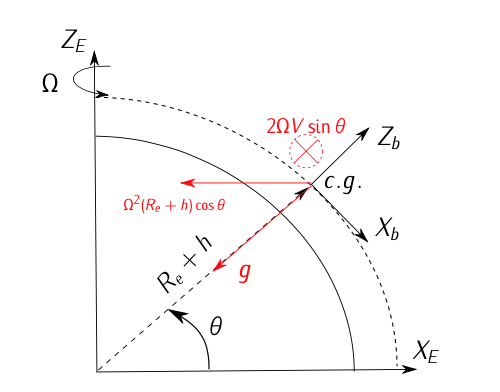
Figura 11.20: Sistema de Navegación Inercial, incluyendo aceleración gravitacional, aceleración de Coriolis (\(2\Omega V\)) y aceleración centrífuga (\(\Omega^2 (R_e + h) \cos (\theta)\)).Por favor, consulte la Figura 11.20.
Deberíamos proyectar el término centrífugo en el eje de la carrocería:
\[Centrifugal: -\Omega^2 (R_e + h) \cos \theta \cdot (\sin \theta \cdot \vec{i}_b + \cos \theta \cdot \vec{k}_b)\]
Entonces, podemos decir:
\[a_x \cdot \vec{i}_b = (a_{ex} - \Omega^2 (R_e + h) \cos \theta \sin \theta) \cdot \vec{i}_b,\]
\[a_y \cdot \vec{j}_b = (a_{ey} + 2\Omega V \sin \theta) \cdot \vec{j}_b,\]
\[a_z \cdot \vec{k}_b = (a_{ez} - g - \Omega^2 (R_e + h) \cos^2 \theta) \cdot \vec{k}_b,\]
donde\(a_{ex}\)\(a_{ey}\), y\(a_{ez}\) son las aceleraciones de la aeronave con respecto a la Tierra y\(a_x\),\(a_y\),\(a_z\) son las aceleraciones absolutas medidas por la IMU.
Háganos saber particularizar a los valores dados, dando como resultado:
\[a_x \cdot \vec{i}_b = (a_{ex} - 0.0168941032554) \cdot \vec{i}_b,\]
\[a_y \cdot \vec{j}_b = (a_{ey} + 0.0257111281143) \cdot \vec{j}_b,\]
\[a_z \cdot \vec{k}_b = (a_{ez} - -9.82689410326) \cdot \vec{k}_b.\]
Siendo las mediciones de los acelerómetros, y\(a_x = 0.9831\ m/s^2\)\(a_y = 0.0257\ m/s^2\), respectivamente\(a_z = -9.8269\ m/s^2\), se tiene: Háganos saber particularizar a los valores dados, resultando:
\[a_{ex} \cdot \vec{i}_b \approx 1 \cdot \vec{i}_b\]
\[a_{ey} \cdot \vec{j}_b \approx 0 \cdot \vec{j}_b\]
\[a_{ez} \cdot \vec{k}_b \approx 0 \cdot \vec{k}_b\]
Así, la aceleración de la aeronave con respecto a la Tierra,\(\vec{a}_e = 1 \cdot \vec{i}_b \ m/s^2\). Esta aceleración es la que se debe utilizar para obtener la posición de la aeronave a través de la doble integración (dadas ciertas condiciones iniciales).
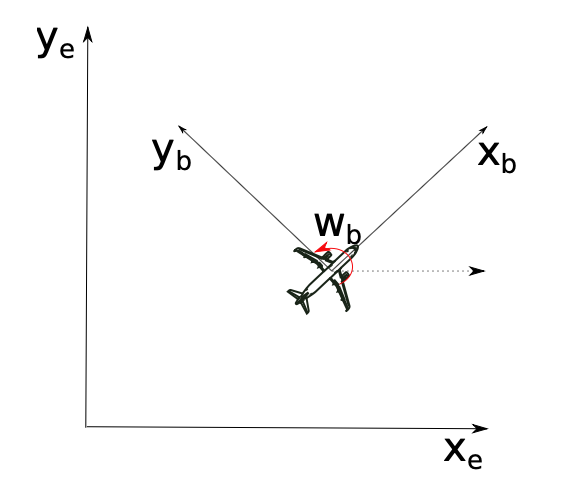
Figura 11.21: Croquis del INS.
Considera una aeronave que vuela a altitud constante como se ilustra en la Figura 11.21. Supongamos que la Tierra puede considerarse plana, no giratoria, 19 y no hay viento (condiciones de calma). Supongamos también que la aeronave está equipada con un sistema de navegación inercial con correa hacia abajo. En el momento\(t\), los acelerómetros y giroscopios están proporcionando las siguientes medidas:
- Velocidad angular:\(\vec{w}_b = w \cdot \vec{k} \approx 0\).
- Fuerzas de la Carrocera-Marco:\(\vec{f}_b = (f_{bx} \cdot \vec{i}_b, f_{by} \cdot \vec{j}_b)\).
Dadas las siguientes condiciones iniciales:
- ángulo inicial de encabezamiento/vía:\(\theta_0\)
- tiempo inicial:\(t_0\);
- posición inicial:\(\vec{r}_0 = (x_0 \cdot \vec{i}_e, y_0 \cdot \vec{j}_e)\);
- velocidad inicial:\(\vec{v}_0 = (v_0 \cdot \vec{i}_b, 0 \cdot \vec{j}_b)\);
Calcular:
- Posición de la aeronave en el momento\(t\).
- Contestar
-
En primer lugar, el lector debe notar que al asumir una Tierra no giratoria, no estamos considerando términos inerciales (Coriolis y Centrífugas). También, debido a que el movimiento se considera horizontal, la gravedad no juega ningún papel en este problema. Por supuesto, un problema realista de Navegación Inercial requeriría realizar el análisis en el ejercicio anterior. En aras de la simplicidad, aquí nos enfocamos en integrar las aceleraciones para obtener la posición (algo que falta en el ejercicio anterior).
Observe que\(\vec{w} = \dot{\theta}\), siendo\(\theta\) un ángulo arbitrario entre una dirección fija, e.g.\(\vec{i}_e\), y la vía de la aeronave, es decir,\(\vec{i}_b\).
Así podemos obtener la variación del\(\theta\) paso del tiempo\(\theta (t)\) simplemente integrando la ecuación fluida:
\[\int_{\theta_0}^{\theta} d\theta = \int_{t_0}^{t} w(t) dt \to \theta (t).\label{eq11.5.26}\]
Ahora, dado que la medición del giroscopio se puede aproximar a cero, es decir\(\vec{w} \approx 0\), la ecuación\(\ref{eq11.5.26}\) rinde:
\[\theta = \theta_0.\]
Los acelerómetros de correa hacia abajo proporcionan mediciones de fuerzas absolutas en el eje del bastidor de carrocería que pueden transformarse fácilmente (bajo las condiciones aquí asumidas) en aceleraciones, es decir,\(\vec{a}_b = (a_{bx} \cdot \vec{i}_b, a_{by} \cdot \vec{j}_b)\).
Ahora bien, para expresar la aceleración absoluta en el marco de referencia de la Tierra, tenemos que aplicar simplemente una rotación:
\[\begin{bmatrix} \vec{a}_{ex} \\ \vec{a}_{ey} \end{bmatrix} = \begin{bmatrix} \cos \theta_0 & -\sin \theta_0 \\ \sin \theta_0 & \cos \theta_0 \end{bmatrix} \cdot \begin{bmatrix} \vec{a}_{bx} \\ \vec{a}_{by} \end{bmatrix}\]
Nosotros ahora que:
\[\dfrac{d\vec{V}}{dt} = \vec{a};\]
\[\dfrac{d\vec{r}}{dt} = d \vec{V}.\]
Al integrar una vez, obtenemos:
\[v_x = v_0 + (a_{xb} \cdot \cos \theta_0 - a_{yb} \cdot \sin \theta_0) \cdot t\]
\[v_y = (a_{yb} \cdot \sin \theta_0 + a_{xb} \cdot \cos \theta_0) \cdot t\]
Al integrarnos dos veces, obtenemos:
\[x = x_0 + v_0 \cdot t + (a_{xb} \cdot \cos \theta_0 - a_{yb} \cdot \sin \theta_0 ) \cdot \dfrac{t^2}{2}\]
\[y = y_0 + (a_{yb} \cdot \sin \theta_0 + a_{xb} \cdot \cos \theta_0) \cdot \dfrac{t^2}{2}\]
Observe que\(t\) se supone que es lo suficientemente pequeño (de hecho, equivalente a la frecuencia de medición) de tal manera que las mediciones pueden considerarse constantes a lo largo del intervalo de tiempo.
18. en aras de la simplicidad, asumimos que los acelerómetros proporcionan directamente aceleraciones después de haber medido fuerzas y haber realizado las transformaciones apropiadas.
19. se puede suponer que tanto los términos centrífugos como los de Coriolis son negables en la fórmula que relaciona la aceleración absoluta y relativa. En otras palabras, las aceleraciones absolutas y relativas pueden considerarse idénticas. Observe que esto es cierto aquí porque hemos considerado que la Tierra no es giratoria.