1.2: Las señales representan información

Última actualización
Guardar como PDF

Page ID: 85356

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

Objetivos de aprendizaje

Una breve discusión de información y señales.
Introducción a la noción de señales continuas y discretas en el tiempo.

Ya sea analógica o digital, la información está representada por la cantidad fundamental en ingeniería eléctrica: la señal. Dicho en términos matemáticos, una señal es meramente una función. Las señales analógicas son de valor continuo; las señales digitales son de valor discreto. La variable independiente de la señal podría ser el tiempo (habla, por ejemplo), el espacio (imágenes), o los enteros (denotando la secuenciación de letras y números en la partitura futbolística).

Señales analógicas

Las señales analógicas suelen ser señales definidas sobre variables independientes continuas. El habla es producida por tus cuerdas vocales excitando resonancias acústicas en tu tracto vocal. El resultado son ondas de presión que se propagan en el aire, y la señal de voz corresponde así a una función que tiene variables independientes de espacio y tiempo y un valor correspondiente a la presión del aire:\[s(x,t) \nonumber \]
Aquí utilizamos notación vectorial\[x \nonumber \]
para denotar coordenadas espaciales.

Cuando grabas a alguien hablando, estás evaluando la señal del habla en una ubicación espacial particular,\[x_{0} \nonumber \]
digamos.

Un ejemplo de la forma de onda resultante\[s(x_{0},t) \nonumber \]

se muestra en la Figura 1.2.1:

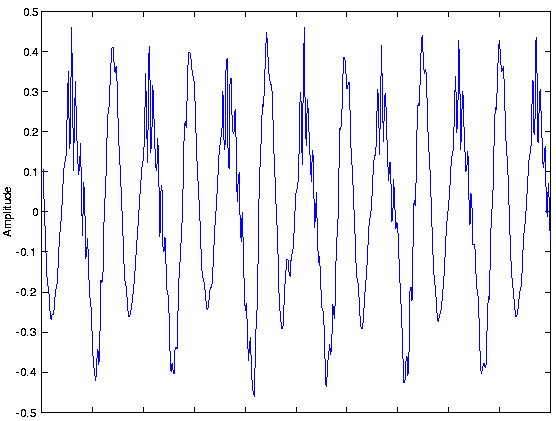
Figura 1.2.1 La amplitud de una señal de voz se relaciona con pequeñas variaciones de presión de aire. Se muestra una grabación de la vocal “e” (como en “discurso”).

Las fotografías son estáticas y son señales de valor continuo definidas sobre el espacio. Las imágenes en blanco y negro solo tienen un valor en cada punto del espacio, lo que equivale a sus propiedades de reflexión óptica. En la Figura 1.2.2 se muestra una imagen, demostrando que ésta (y todas las demás imágenes también) son funciones de dos variables espaciales independientes.

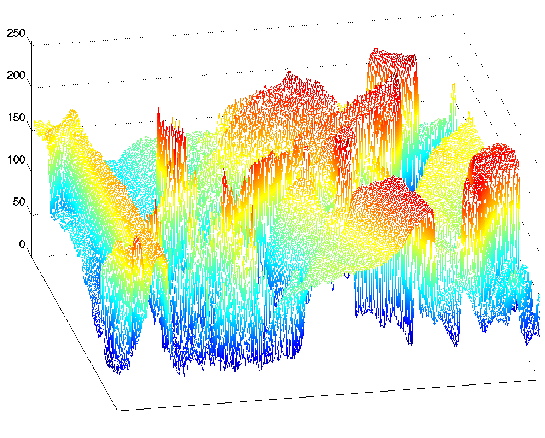
a) b)

Figura 1.2.2 A la izquierda se encuentra la imagen clásica de Lena, la cual se utiliza ubicuamente como imagen de prueba. Contiene líneas rectas y curvas, textura complicada y una cara. A la derecha hay una visualización en perspectiva de la imagen de Lena como señal: una función de dos variables espaciales. Los colores simplemente ayudan a mostrar qué valores de señal son aproximadamente del mismo tamaño. En esta imagen, los valores de señal oscilan entre 0 y 255; ¿por qué es eso?

Las imágenes en color tienen valores que expresan cómo la reflectividad depende del espectro óptico. Hace mucho tiempo, los pintores descubrieron que la mezcla de combinaciones de los llamados colores primarios —rojo, amarillo y azul— puede producir imágenes en color muy realistas. Así, las imágenes de hoy en día suelen ser consideradas como que tienen tres valores en cada punto del espacio, pero se utiliza un conjunto diferente de colores: Qué cantidad de rojo, verde y azul está presente. Matemáticamente, las imágenes en color son señales multivaloradas, con valores vectoriales:

\[s(x)=\left ( r(x),g(x),b(x) \right )^{T} \nonumber \]

Abundan casos interesantes donde la señal analógica no depende de una variable continua, como el tiempo, sino de una variable discreta. Por ejemplo, las lecturas de temperatura tomadas cada hora tienen valores continuos analógicos, pero la variable independiente de la señal es (esencialmente) los números enteros.

Señales Digitales

La palabra “digital” significa valor discreto e implica que la señal tiene una variable independiente de valor entero. La información digital incluye números y símbolos (caracteres escritos en el teclado, por ejemplo). Las computadoras se basan en la representación digital de la información para manipular y transformar la información. Los símbolos no tienen un valor numérico, y cada uno está representado por un número único. El código de caracteres ASCII tiene los caracteres en mayúsculas y minúsculas, los números, signos de puntuación y varios otros símbolos representados por un entero de siete bits. Por ejemplo, el código ASCII representa la letra

nul

soh

stx

etx

eot

enq

ack

bel

por lo

dle

dc1

dc2

dc3

dc4

nak

syn

etb

auto

sub

esc

nosotros

“

(

)

;

[

]

{

}

del

Tabla 1.2.1 La tabla de traducción ASCII muestra cómo los caracteres estándar del teclado son representados por números enteros. En pares de columnas, esta tabla muestra primero el llamado código de 7 bits (¿cuántos caracteres hay en un código de siete bits?) , entonces el carácter que representa el número. Los códigos numéricos se representan en notación hexadecimal (base-16). Los caracteres mnemónicos corresponden a caracteres de control, algunos de los cuales pueden ser familiares (como cr para retorno de carro) y otros no (bel significa una “campana”).

Colaborador

ContribeeOpenStax