4.2: Serie compleja de Fourier
- Page ID
- 85299
- Definición de la serie compleja de Fourier.
En un módulo anterior, demostramos que una onda cuadrada podría expresarse como una superposición de pulsos. Tan útil como fue esta descomposición en este ejemplo, no generaliza bien a otras señales periódicas: ¿Cómo puede una superposición de pulsos igualar una señal suave como una sinusoide? Debido a la importancia de los sinusoides para los sistemas lineales, podría preguntarse si podrían sumarse para representar una gran cantidad de señales periódicas. Estarías en lo cierto y en buena compañía también. Euler y Gauss en particular se preocuparon por este problema, y Jean Baptiste Fourier obtuvo el crédito a pesar de que los difíciles problemas matemáticos no se resolvieron hasta más tarde. Trabajaron en lo que ahora se conoce como la serie de Fourier: representar cualquier señal periódica como superposición de sinusoides.
Pero la serie de Fourier va mucho más allá de ser otro método de descomposición de señales. Más bien, la serie de Fourier comienza nuestro viaje para apreciar cómo se puede describir una señal en el dominio del tiempo o en el dominio de la frecuencia sin compromiso.
Sea s (t) una señal periódica con periodo T. Queremos mostrar que las señales periódicas, incluso aquellas que tienen segmentos de valor constante como una onda cuadrada, pueden expresarse como suma de ondas sinusoidales relacionadas armónicamente: sinusoides que tienen frecuencias que son múltiplos enteros de la frecuencia fundamental. Debido a que la señal tiene periodo T, la frecuencia fundamental es 1/T. La serie compleja de Fourier expresa la señal como una superposición de exponenciales complejos que tienen frecuencias:
\[\frac{k}{T},k=\left \{ ....,-1,0,1,....\right \} \nonumber \]
\[s(t)=\sum_{k=-\infty }^{\infty }c_{k}e^{i\frac{2\pi kt}{T}} \nonumber \]
con
\[c_{k}=\frac{1}{2}\left ( a_{k}-ib_{k}\right ) \nonumber \]
Las partes reales e imaginarias de los coeficientes de Fourier c k se escriben de esta manera inusual por conveniencia en la definición de la serie clásica de Fourier. El coeficiente cero es igual al valor promedio de la señal y es real- valorado para señales de valor real: c 0 =a 0. La familia de funciones
\[\left \{ e^{i\frac{2\pi kt}{T}} \right \} \nonumber \]
se llaman funciones base y forman la base de la serie de Fourier. No importa cuál sea la señal periódica, estas funciones están siempre presentes y forman los bloques de construcción de la representación. Dependen del periodo de señal T, y están indexados por k.
Suponiendo que conocemos el periodo, conocer los coeficientes de Fourier equivale a conocer la señal. Por lo tanto, no hace diferencia si tenemos una caracterización de la señal en el dominio del tiempo o en el dominio de la frecuencia.
¿Cuál es la serie compleja de Fourier para una sinusoide?
Solución
Debido a la relación de Euler,
\[\sin (2\pi ft)=\frac{1}{2i}e^{i2\pi ft}-\frac{1}{2i}e^{-(i2\pi ft)} \nonumber \]
Por lo tanto,
\[c_{1}=\frac{1}{2i},\; c_{-1}=-\frac{1}{2i} \nonumber \]
y los demás coeficientes son cero.
Para encontrar los coeficientes de Fourier, observamos la propiedad de ortogonalidad
\[\int_{0}^{T}e^{i\frac{2\pi kt}{T}} e^{(-i)\frac{2\pi kt}{T}} dt=\begin{cases} T & \text{ if } k=l \\ 0&\text{ if } k\neq l \end{cases} \nonumber \]
Suponiendo por el momento que la serie compleja de Fourier “funciona”, podemos encontrar los coeficientes complejos de Fourier de una señal, su espectro, explotando las propiedades de ortogonalidad de exponenciales complejos armónicamente relacionados.
Simplemente multiplique cada lado de la ecuación de la Serie de Fourier por
\[e^{(-i2\pi lt)} \nonumber \]
e integrar a lo largo del intervalo [0, T].
\[c_{k}=\frac{1}{T}\int_{0}^{T}s(t)e^{-\left ( i\frac{2\pi kt}{T}\right )} dt \nonumber \]
\[c_{0}=\frac{1}{T}\int_{0}^{T}s(t)dt \nonumber \]
Encontrar los coeficientes de la serie de Fourier para la onda cuadrada T (t) es muy sencillo. Matemáticamente, esta señal se puede expresar como
\[sq_{T}(t)=\begin{cases} 1 & \text{ if } 0< t< \frac{T}{2} \\ -1& \text{ if } \frac{T}{2}< t< T \end{cases} \nonumber \]
La expresión para los coeficientes de Fourier tiene la forma
\[c_{k}=\frac{1}{T}\int_{0}^{\frac{T}{2}}e^{-\left ( i\frac{2\pi kt}{T}\right )} dt-\frac{1}{T}\int_{\frac{T}{2}}^{T}e^{-\left ( i\frac{2\pi kt}{T}\right )} dt \nonumber \]
Al integrar una expresión que contenga i, trátela como cualquier otra constante.
Las dos integrales son muy similares, una igualando la negativa de la otra. La expresión final se convierte
\[c_{k}=\frac{-2}{i2\pi k}\left ( (-1)^{k}-1 \right )\\ c_{k}=\begin{cases} \frac{2}{i\pi k} & \text{ if } k=odd \\ 0 & \text{ if } k=even \end{cases} \nonumber \]
\[sq(t)=\sum_{k\in \left \{ ...,-3,-1,1,3,... \right \}}\frac{2}{i2\pi k}e^{(i)\frac{2\pi kt}{T}} \nonumber \]
En consecuencia, la onda cuadrada equivale a una suma de exponenciales complejos, pero solo aquellos que tienen frecuencias iguales a múltiplos impares de la frecuencia fundamental 1/T. Los coeficientes disminuyen lentamente a medida que aumenta el índice de frecuencia k. Este índice corresponde al k-ésimo armónico del periodo de la señal.
Propiedades del espectro de la serie de Fourier
El espectro de la serie de Fourier de una señal c k tiene propiedades interesantes.
Si s (t) es real,
\[c_{k}=\overline{c_{-k}} \nonumber \]
Las señales periódicas de valor real tienen espectros conjugados-simétricos.
Este resultado se desprende de la integral que calcula el c k a partir de la señal. Además, este resultado significa que:
\[\Re (c_{k})=\Re ({c_{-k}}) \nonumber \]
La parte real de los coeficientes de Fourier para las señales de valor real es pareja. Del mismo modo,
\[\Im (c_{k})=\Im ({c_{-k}}) \nonumber \]
Las partes imaginarias de los coeficientes de Fourier tienen simetría impar. En consecuencia, si se le dan los coeficientes de Fourier para índices positivos y cero y se le dice que la señal es de valor real, puede encontrar los coeficientes indexados negativos, de ahí todo el espectro. Este tipo de simetría,
\[c_{k}=\overline{c_{-k}} \nonumber \]
se conoce como simetría conjugada.
Si s (-t) = s (t), que dice que la señal tiene incluso simetría sobre el origen,
\[c_{-k}=c_{k} \nonumber \]
Dada la propiedad anterior para las señales de valor real, los coeficientes de Fourier de las señales pares son de valor real. Una expansión de Fourier de valor real equivale a una expansión en términos de solo cosenos, que es el ejemplo más simple de una señal par.
Si s (-t) = - s (t), que dice que la señal tiene simetría impar,
\[c_{-k}=-c_{k} \nonumber \]
Por lo tanto, los coeficientes de Fourier son puramente imaginarios. La onda cuadrada es un gran ejemplo de una señal impar-simétrica.
Los coeficientes espectrales para una señal periódica retardada por τ, s (t-τ), son:
\[c_{k}e^{-\frac{i2\pi k\tau }{T}} \nonumber \]
donde c k denota el espectro de s (t).
Retrasar una señal por τ segundos resulta en un espectro que tiene un desplazamiento de fase lineal\[-\frac{2\pi k\tau }{T} \nonumber \] en comparación con el espectro de la señal no retardada. Tenga en cuenta que la magnitud espectral no se ve afectada. Mostrar esta propiedad es fácil.
\[\frac{1}{T}\int_{0}^{T}s(t-\tau )e^{(-i)\frac{2\pi kt}{T}} dt=\frac{1}{T}\int_{-\tau }^{T-\tau }s(t)e^{(-i)\frac{2\pi k(t+\tau )}{T}} dt \nonumber \]
\[\therefore \; \; \; \; \; \frac{1}{T}\int_{0}^{T}s(t-\tau )e^{(-i)\frac{2\pi kt}{T}} dt=\frac{1}{T}e^{(-i)\frac{2\pi kt}{T}} \int_{-\tau }^{T-\tau }s(t)e^{(-i)\frac{2\pi kt}{T}} dt \nonumber \]
Tenga en cuenta que el rango de integración se extiende a lo largo de un período del integrando. En consecuencia, no debería importar cómo nos integremos a lo largo de un periodo, lo que significa que:
\[\int_{-\tau }^{T-\tau }(\cdot )dt=\int_{0}^{T}(\cdot )dt \nonumber \]
y tenemos nuestro resultado.
La serie compleja de Fourier obedece al Teorema de Parseval, uno de los resultados más importantes en el análisis de señales. Este resultado matemático general dice que se puede calcular la potencia de una señal ya sea en el dominio del tiempo o en el dominio de la frecuencia.
Teorema de Parseval
La potencia promedio calculada en el dominio del tiempo es igual a la potencia calculada en el dominio de frecuencia.
\[\frac{1}{T}\int_{0}^{T}s^{2}(t)dt=\sum_{-\infty }^{\infty }\left ( \left | c_{k} \right | \right )^{2} \nonumber \]
Este resultado es una reexpresión (más simple) de cómo calcular la potencia de una señal que con la expresión de potencia de la serie de Fourier de valor real.
Calculemos los coeficientes de Fourier de la señal de pulso periódico que se muestra en la Figura 4.2.1 a continuación.
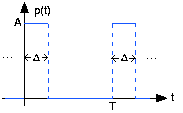
El ancho de pulso es Δ, el periodo T y la amplitud A. El espectro complejo de Fourier de esta señal viene dado por:
\[c_{k}=\frac{1}{T}\int_{0}^{\Delta }Ae^{-\frac{i2\pi kt}{T}}dt=-\left ( \frac{A}{i2\pi k}\left ( e^{-\frac{i2\pi \Delta }{T}} -1\right ) \right ) \nonumber \]
En este punto, simplificar esta expresión requiere conocer una propiedad interesante.
\[1-e^{-(i\theta )}=e^{-\frac{i\theta }{2}}\left ( e^{\frac{i\theta }{2}}-e^{-\frac{i\theta }{2}}\right )=e^{-\frac{i\theta }{2}}2i\sin \left ( \frac{\theta }{2}\right ) \nonumber \]
Armados con este resultado, simplemente podemos expresar los coeficientes de la serie de Fourier para nuestra secuencia de pulsos.
\[c_{k}=Ae^{-\frac{i\pi k\Delta }{T}}\frac{\sin \left ( \frac{\pi k\Delta }{T} \right )}{\pi k} \nonumber \]
Debido a que esta señal es de valor real, encontramos que los coeficientes tienen simetría conjugada:
\[c_{k}=\overline{c_{-k}} \nonumber \]
La señal de pulso periódica no tiene simetría par ni impar; en consecuencia, no existe simetría adicional en el espectro. Debido a que el espectro es complejo valorado, para trazarlo necesitamos calcular su magnitud y fase.
\[\left | c_{k}\right |=A\left | \frac{\sin \left ( \frac{\pi k\Delta }{T} \right )}{\pi k} \right | \nonumber \]
\[\angle c_{k}=-\frac{\pi k\Delta }{T}+\pi \, neg\left | \frac{\sin \left ( \frac{\pi k\Delta }{T} \right )}{\pi k} \right |\, sign(k) \nonumber \]
La función neg (•) es igual a -1 si su argumento es negativo y cero en caso contrario. La expresión algo complicada para la fase resulta porque el término seno puede ser negativo; las magnitudes deben ser positivas, dejando que los valores negativos ocasionales se tengan en cuenta como un desplazamiento de fase de
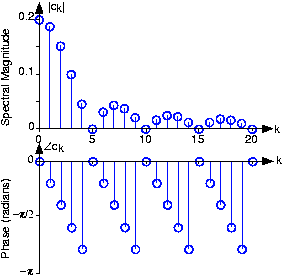
La magnitud y fase del espectro de la secuencia de pulsos periódicos se muestra para los índices de frecuencia positiva. Aquí Δ/T = 0.2 y A = 1
También hay que señalar la presencia de un término de fase lineal (el primer término en c k es proporcional a la frecuencia K/t). Comparando este término con el predicho de retrasar una señal, un retraso de Δ/2 está presente en nuestra señal. Avanzar la señal en esta cantidad centra el pulso alrededor del origen, dejando una señal par, lo que a su vez significa que su espectro es de valor real. Así, nuestro espectro calculado es consistente con las propiedades del espectro de Fourier.
¿Cuál es el valor de c 0? Recordando que este coeficiente espectral corresponde al valor promedio de la señal, ¿tiene sentido tu respuesta?
Solución
\[c_{0}=\frac{A\Delta }{T} \nonumber \]
Esta cantidad corresponde claramente al valor promedio de la señal de pulso periódico.
La gráfica de fases que se muestra en la Figura 4.2.2 requiere alguna explicación ya que no parece estar de acuerdo con lo que sugiere la ecuación para c k. Ahí, la fase tiene un componente lineal, con un salto decada vez que el término sinusoidal cambia de signo. Debemos darnos cuenta de que cualquier múltiplo entero de 2se puede agregar a una fase en cada frecuencia sin afectar el valor del espectro complejo. Vemos que en el índice de frecuencia 4 la fase es casi -. La fase en el índice 5 no está definida porque la magnitud es cero en este ejemplo. En el índice 6, la fórmula sugiere que la fase del término lineal debe ser menor que -(más negativo). Además, esperamos un cambio de -en la fase entre los índices 4 y 6. Así, el valor de fase predicho por la fórmula es un poco menor que - (2). Porque podemos agregar 2sin afectar el valor del espectro en el índice 6, el resultado es un número ligeramente negativo como se muestra. Así, la fórmula y la trama sí están de acuerdo. En cálculos de fase como los realizados en MATLAB, los valores generalmente se limitan al rango [-,]añadiendo algunos (posiblemente negativos) múltiplo de 2a cada valor de fase.