4.7: Filtrado de señales periódicas

Objetivos de aprendizaje

• Este módulo demuestra el efecto que un filtro invariable en el tiempo puede tener en las formas de onda periódicas.

La representación en serie de Fourier de una señal periódica facilita determinar cómo un filtro lineal e invariable en el tiempo reconfigura tales señales en general. La propiedad fundamental de un sistema lineal es que su relación entrada-salida obedece a la superposición:

$$L\left ( a_{1}s_{1}(t)+a_{2}s_{2}(t) \right )=a_{1}L\left ( s_{1}(t) \right )+a_{2}L\left ( s_{2}(t) \right ) \nonumber$$

Debido a que la serie de Fourier representa una señal periódica como una combinación lineal de exponenciales complejos, podemos explotar la propiedad de superposición. Además, encontramos para los circuitos lineales que su salida a una entrada exponencial compleja es solo la respuesta de frecuencia evaluada a la frecuencia de la señal multiplicada por la exponencial compleja. Dicho matemáticamente, si:

$$x(t)=e^{i\frac{2\pi kt}{T}} \nonumber$$

luego la salida

$$y(t)=H\left ( \frac{k}{T} \right )e^{i\frac{2\pi kt}{T}} \nonumber$$

porque

$$f= \frac{k}{T} \nonumber$$

Así, si x (t) es periódico teniendo así una serie de Fourier, la salida de un circuito lineal a esta señal será la superposición de la salida a cada componente.

$$y(t)=\sum_{k=-\infty }^{\infty }c_{k}H\left ( \frac{k}{T} \right )e^{i\frac{2\pi kt}{T}} \nonumber$$

Así, la salida tiene una serie de Fourier, lo que significa que también es periódica. Sus coeficientes de Fourier son iguales a:

$$c_{k}H\left ( \frac{k}{T} \right ) \nonumber$$

Para obtener el espectro de la salida, simplemente multiplicamos el espectro de entrada por la respuesta de frecuencia. El circuito modifica la magnitud y fase de cada coeficiente de Fourier. Tenga en cuenta especialmente que si bien los coeficientes de Fourier no dependen del período de la señal, la función de transferencia del circuito sí depende de la frecuencia, lo que significa que la salida del circuito diferirá a medida que el período varía.

Figura 4.7.1a Señal de pulso periódica

Figura 4.7.1b Los gráficos superiores muestran el espectro de la señal de pulso para varias frecuencias de corte. Las gráficas inferiores muestran las señales de salida del filtro.

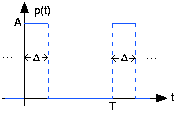
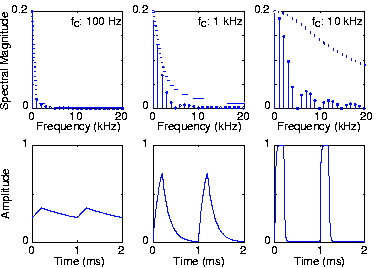
En la Figura 4.7.1b anterior, una señal de pulso periódica, tal como se muestra en la parte izquierda donde (Δ/2 = 0.2), sirve como entrada a un filtro de paso bajo RC. El periodo de entrada fue de 1ms (milisegundo). La frecuencia de corte del filtro se estableció en los diversos valores indicados en la fila superior, los cuales muestran el espectro de la señal de salida y la función de transferencia del filtro. La fila inferior muestra la señal de salida derivada de los coeficientes de la serie de Fourier mostrados en la fila superior.

Ejemplo$\PageIndex{1}$:

La señal de pulso periódica que se muestra a la izquierda de arriba sirve como entrada a un circuito RC que tiene la función de transferencia

$$H(f)=\frac{1}{1+i2\pi fRC} \nonumber$$

La Figura 4.7.1b muestra los cambios de salida a medida que variamos la frecuencia de corte del filtro. Observe cómo el espectro de la señal se extiende muy por encima de su frecuencia fundamental. Tener una frecuencia de corte diez veces mayor que la fundamental cambia perceptiblemente la forma de onda de salida, redondeando los bordes de entrada y salida. A medida que disminuye la frecuencia de corte (centro, luego a la izquierda), el redondeo se vuelve más prominente, con la forma de onda más a la izquierda mostrando una pequeña ondulación.

Ejercicio$\PageIndex{1}$

¿Cuál es el valor promedio de cada forma de onda de salida? La respuesta correcta puede sorprenderte.

Solución

Debido a que la ganancia del filtro a frecuencia cero es igual a uno, los valores de salida promedio son iguales a los valores de entrada promedio respectivos.

Este ejemplo también ilustra el impacto que un filtro de paso bajo puede tener en una forma de onda. El filtro RC simple utilizado aquí tiene una respuesta de frecuencia bastante gradual, lo que significa que los armónicos más altos se suprimen suavemente. Posteriormente, describiremos filtros que tienen respuestas de frecuencia mucho más rápidamente variables, permitiendo una selección mucho más dramática de los coeficientes de Fourier de la entrada.

Más importante aún, hemos calculado la salida de un circuito a una entrada periódica sin escribir, mucho menos resolver, la ecuación diferencial que rige el comportamiento del circuito. Además, realizamos estos cálculos íntegramente en el dominio de la frecuencia. Usando series de Fourier, podemos calcular cómo responderá cualquier circuito lineal a una entrada periódica.