5.17: Problemas de procesamiento de señales digitales

Objetivos de aprendizaje

• Problemas de práctica.

Muestreo y Filtración=?

La señal s (t) está limitada en banda a 4 kHz. Lo queremos muestrear, pero ha sido sometido a diversas manipulaciones de procesamiento de señales.

1. ¿Qué frecuencia de muestreo (si alguna funciona) se puede utilizar para muestrear el resultado de pasar s (t) a través de un filtro de paso alto RC con R = 10kΩ y C = 8nF?
2. ¿Qué frecuencia de muestreo (si hay alguna obra) se puede utilizar para muestrear la derivada de s (t)?
3. La señal s (t) ha sido modulada por una sinusoide de 8 kHz que tiene una fase desconocida: la señal resultante es\[s(t)\sin (2\pi f_{0}t+\varphi ) \nonumber \] con f ₀ = 8kHz y φ=? ¿Se puede muestrear la señal modulada para que la señal original pueda recuperarse de la señal modulada independientemente del valor de fase φ? Si es así, mostrar cómo y encontrar la frecuencia de muestreo más pequeña que se pueda utilizar; si no, mostrar por qué no.

Muestreo no estándar

El uso de las propiedades de la serie de Fourier puede facilitar la búsqueda del espectro de una señal.

1. Supongamos que una señal s (t) es periódica con el periodo T. Si c _k representa los coeficientes de la serie de Fourier de la señal, ¿cuáles son los coeficientes de la serie de Fourier de\[s\left ( t-\frac{T}{2} \right ) \nonumber \]
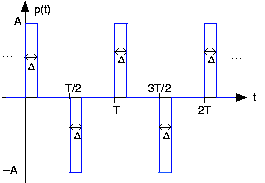
2. Encuentre la serie de Fourier de la señal p (t) que se muestra en la Figura 5.17.1.
3. Supongamos que esta señal se utiliza para muestrear una señal de banda limitada a 1/T Hz. Encuentre una expresión para y esboce el espectro de la señal muestreada.
4. ¿Se produce el aliasing? Si es así, puede un cambio en la frecuencia de muestreo evitar el aliasing; si no, mostrar cómo se puede recuperar la señal de estas muestras.

Figura5.17.1

Un esquema de muestreo diferente

Un ingeniero de procesamiento de señales de Texas A&M afirma haber desarrollado un esquema de muestreo mejorado. Multiplica la señal de banda limitada por la señal de pulso periódica representada para realizar el muestreo.

Figura 5.17.2

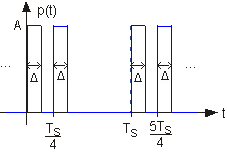
1. Encuentra el espectro de Fourier de esta señal.
2. ¿Funcionará este esquema? Si es así, ¿cómo debería relacionarse T _S con el ancho de banda de la señal? Si no, ¿por qué no?

Muestreo paso banda

La señal s (t) tiene el espectro indicado.

Figura 5.17.3

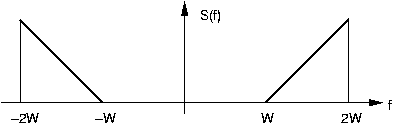
1. ¿Cuál es la frecuencia de muestreo mínima para esta señal sugerida por el Teorema de Muestreo?
2. Debido a la estructura particular de este espectro, uno se pregunta si se podría utilizar una tasa de muestreo más baja. Demostrar que efectivamente este es el caso, y encontrar el sistema que reconstruye s (t) a partir de sus muestras.

Muestreo de señales

Si una señal está limitada en banda a W Hz, podemos tomarla a cualquier velocidad

\[\frac{1}{T_{S}}> 2W \nonumber \]

y recuperar la forma de onda exactamente. Esta afirmación del Teorema de Muestreo se puede tomar en el sentido de que toda la información sobre la señal original puede ser extraída de las muestras. Si bien es cierto en principio, sí hay que tener cuidado de cómo lo hace. Además del valor rms de una señal, un aspecto importante de una señal es su valor pico, que es igual a

\[\max \left \{ \left | s(t) \right | \right \} \nonumber \]

1. Sea s (t) una sinusoide que tenga frecuencia W Hz. Si lo muestreamos precisamente a la velocidad Nyquist, ¿con qué precisión transmiten las muestras la amplitud de la sinusoide? En otras palabras, encuentra el peor ejemplo de los casos.
2. ¿Qué tan rápido necesitarías muestrear para que la estimación de amplitud esté dentro del 5% del valor verdadero?
3. Otro problema en el muestreo es la cuantificación de amplitud inherente producida por los convertidores A/D. Supongamos que el voltaje máximo permitido por el convertidor es V _max volts y que cuantifica amplitudes a b bits. Podemos expresar la muestra cuantificada\[Q(s(nT_{S}))\; as\; s(nT_{S})+\varepsilon (t) \nonumber \] donde ε (t) representa el error de cuantificación en la ^n-ésima muestra. Suponiendo que el convertidor redondea, ¿qué tan grande es el error máximo de cuantificación?
4. Podemos describir el error de cuantificación como ruido, con una potencia proporcional al cuadrado del error máximo. ¿Cuál es la relación señal-ruido del error de cuantificación para una sinusoide de rango completo? Expresa tu resultado en decibelios.

Error de hardware

Un convertidor A/D tiene un curioso problema de hardware: Cada otro pulso de muestreo tiene la mitad de su amplitud normal.

Figura 5.17.4

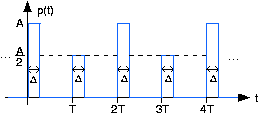
1. Encuentra la serie de Fourier para esta señal.
2. ¿Se puede usar esta señal para muestrear una señal de banda limitada que tiene la frecuencia más alta\[W=\frac{1}{2T} \nonumber \]

Convertidor D/A simple

Los convertidores comerciales de digital a analógico no funcionan de esta manera, pero un circuito simple ilustra cómo funcionan. Supongamos que tenemos un convertidor de B bits. Por lo tanto, queremos convertir números que tienen una representación de B bits en un voltaje proporcional a ese número. El primer paso dado por nuestro convertidor simple es representar el número por una secuencia de pulsos B que ocurren en múltiplos de un intervalo de tiempo T. La presencia de un pulso indica un “1” en la posición de bit correspondiente, y la ausencia de pulso significa que se produjo un “0”. Para un convertidor de 4 bits, el número 13 tiene la representación binaria 1101

\[13_{10}=1\times 2^{3}+1\times 2^{2}+0\times 2^{1}+1\times 2^{0} \nonumber \]

y estaría representado por la secuencia de pulsos representada. Tenga en cuenta que la secuencia de pulsos está “al revés” de la representación binaria. Ya veremos por qué es eso.

Figura 5.17.5

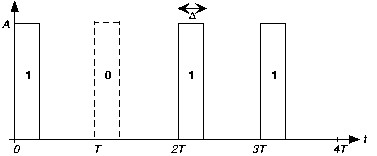
Esta señal sirve como entrada a un filtro de paso bajo RC de primer orden. Queremos diseñar el filtro y los parámetros Δ y T para que el voltaje de salida en el tiempo 4T (para un convertidor de 4 bits) sea proporcional al número. Esta combinación de creación de pulsos y filtrado constituye nuestro sencillo convertidor D/A. Los requisitos son

• El voltaje en el tiempo t = 4T debería disminuir en un factor de 2 cuanto más se produzca el pulso a partir de este momento. En otras palabras, el voltaje debido a un pulso a 3T debe ser el doble que el de un pulso producido a 2T, que a su vez es el doble que el de un pulso en T, etc.
• El convertidor D/A de 4 bits debe soportar una frecuencia de muestreo de 10 kHz.

1. Mostrar el circuito que funciona. ¿Cómo cambian los parámetros del convertidor con la frecuencia de muestreo y el número de bits en el convertidor?

Transformadas de Fourier en Tiempo Discreto

Encuentre las transformadas de Fourier de las siguientes secuencias, donde s (n) es alguna secuencia que tiene transformada de Fourier\[S(e^{i2\pi f}) \nonumber \]

1. \[(-1)^{n}s(n) \nonumber \]
2. \[s(n)\cos (2\pi f_{0}n) \nonumber \]
3. \[x(n)=\begin{cases} s(\frac{n}{2}) & \text{ if } n\; even \\ 0 & \text{ if } n\; odd \end{cases} \nonumber \]
4. \[ns(n) \nonumber \]

Espectros de señales de duración finita

Encuentra los espectros indicados para las siguientes señales.

1. La transformada de Fourier en tiempo discreto de\[s(n)=\begin{cases} \cos ^{2} \left ( \frac{\pi }{4} n\right )& \text{ if } n= \left \{ -1,0,1 \right \}\\ 0 & \text{ if } otherwise \end{cases} \nonumber \]
2. La transformada de Fourier en tiempo discreto de\[s(n)=\begin{cases} n & \text{ if } n= \left \{ -2,-1,0,1,2 \right \}\\ 0 & \text{ if } otherwise \end{cases} \nonumber \]
3. La transformada de Fourier en tiempo discreto de\[s(n)=\begin{cases} \sin \left ( \frac{\pi }{4} n\right ) & \text{ if } n= \left \{ 0,...,7 \right \}\\ 0 & \text{ if } otherwise \end{cases} \nonumber \]
4. La longitud-8 DFT de la señal anterior.

Sólo silbando

A Sammy le encanta silbar y decide grabar y analizar su silbido en laboratorio. Es un muy buen silbador; su silbato es una sinusoide pura que puede ser descrita por

\[s_{a}(t)=\sin (4000t) \nonumber \]

Para analizar el espectro, toma muestras de su silbato registrado con un intervalo de muestreo de

\[T_{S}=2.5\times 10^{-4} \nonumber \]

para obtener

\[s(n)=s_{a}(nT_{S}) \nonumber \]

Sammy (sabiamente) decide analizar algunas muestras a la vez, por lo que agarra 30 muestras consecutivas, pero elegidas arbitrariamente,. Llama a esta secuencia x (n) y se da cuenta de que puede escribirla como

\[x(n)=\sin (4000nT_{s}+\theta ),\; n=\left \{ 0,...,29 \right \} \nonumber \]

1. ¿Sammy probó por debajo o en exceso su silbato?
2. ¿Cuál es la transformada de Fourier en tiempo discreto de x (n) y cómo depende de θ?
3. ¿Cómo depende la DFT de 32 puntos de x (n) de θ?

Filtrado de Tiempo Discreto

Podemos encontrar la relación entrada-salida para un filtro de tiempo discreto mucho más fácilmente que para filtros analógicos. La idea clave es que una secuencia se pueda escribir como una combinación lineal ponderada de muestras unitarias.

1. Mostrar que\[x(n)=\sum _{i}x(i)\delta (n-i) \nonumber \] donde δ (n) es la unidad-muestra. \[\delta (n)=\begin{cases} 1 & \text{ if } n=0 \\ 0 & \text{ if } otherwise \end{cases} \nonumber \]
2. Si h (n) denota la respuesta de muestra unitaria, la salida de un filtro lineal de tiempo discreto, invariante de desplazamiento a una entrada de muestra unitaria, encuentre una expresión para la salida.
3. En particular, supongamos que nuestro filtro es FIR, con la respuesta unidad-muestra teniendo duración q+1. Si la entrada tiene duración N, ¿cuál es la duración de la salida del filtro a esta señal?
4. Deja que el filtro sea un promedio de vagón:\[h(n)=\frac{1}{q+1}\; for\; n=\left \{ 0,...,q \right \} \nonumber \] y cero de lo contrario. Deja que la entrada sea un pulso de unidad de altura y duración N. Encuentra la salida del filtro cuando\[N=\frac{q+1}{2} \nonumber \] q un entero impar.

Un filtro digital

Un filtro digital tiene la respuesta unidad-muestra representada.

Figura 5.17.6

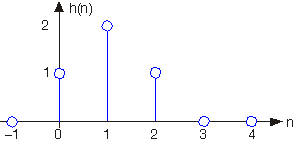
1. ¿Cuál es la ecuación de diferencia que define la relación input-output de este filtro?
2. ¿Cuál es la función de transferencia de este filtro?
3. Cuál es la salida del filtro cuando la entrada es\[\sin \left ( \frac{\pi n}{4} \right ) \nonumber \]

Un filtro especial de tiempo discreto

Considere un filtro FIR gobernado por la ecuación de diferencia

\[y(n)=\frac{1}{3}x(n+2)+\frac{2}{3}x(n+1)+x(n)+\frac{2}{3}x(n-1)+\frac{1}{3}x(n-2) \nonumber \]

1. Encuentra la respuesta unidad-muestra de este filtro.
2. Encuentra la función de transferencia de este filtro. Caracterizar esta función de transferencia (es decir, en qué categoría de filtro clásica se encuentra).
3. Supongamos que tomamos una secuencia y la estiramos por un factor de tres. \[x(n)=\begin{cases} s(\frac{n}{3}) & \text{ if } \forall m,m=\left \{ ...,-1,0,1,... \right \} :(n-3m)\\ 0 & \text{ if } otherwise \end{cases} \nonumber \]
   1. Esbozar la secuencia x (n) para algunos ejemplos s (n).
   2. ¿Cuál es la salida del filtro a esta entrada?
   3. En particular, ¿cuál es la salida en los índices donde la entrada x (n) es intencionalmente cero?
   4. Ahora, ¿cómo caracterizarías a este sistema?

Simulación del mundo real

Gran parte de la física se rige por ecuaciones diferenciales, y queremos usar métodos de procesamiento de señales para simular problemas físicos. La idea es sustituir la derivada por una aproximación discreta en el tiempo y resolver la ecuación diferencial resultante. Por ejemplo, supongamos que tenemos la ecuación diferencial

\[\frac{\mathrm{d} y(t)}{\mathrm{d} t}+ay(t)=x(t) \nonumber \]

y aproximamos la derivada por

\[\frac{\mathrm{d} y(t)}{\mathrm{d} t}\mid\ _{t=nT}\simeq \frac{y(nT)-y((n-1)T)}{T} \nonumber \]

donde T equivale esencialmente a un intervalo de muestreo.

1. ¿Cuál es la ecuación de diferencia que se debe resolver para aproximar la ecuación diferencial?
2. Cuando x (t) = u (t), el paso de la unidad, ¿cuál será la salida simulada?
3. Suponiendo que x (t) es una sinusoide, ¿cómo se debe elegir el intervalo de muestreo T para que la aproximación funcione bien?

Derivados

La derivada de una secuencia tiene poco sentido, pero aún así, podemos aproximarla. El filtro digital descrito por la ecuación de diferencia

\[y(n)=x(n)-x(n-1) \nonumber \]

se asemeja a la fórmula derivada. Queremos explorar lo bien que funciona.

1. ¿Cuál es la función de transferencia de este filtro?
2. ¿Cuál es la salida del filtro a la salida del triángulo representado?

Figura 5.17.7

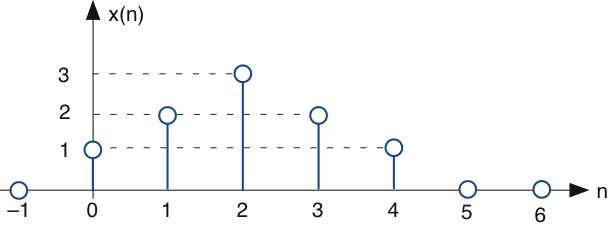
3. Supongamos que la señal x (n) es una señal analógica muestreada: ¿\[x(n)=x(nT_{S}) \nonumber \]Bajo qué condiciones actuará el filtro como un diferenciador? En otras palabras, cuando y (n) será proporcional a\[\frac{\mathrm{d} x(t)}{\mathrm{d} t}\mid\ _{t=nT_{S}} \nonumber \]

El DFT

Exploremos el DFT y sus propiedades.

1. ¿Cuál es la longitud- K DFT de longitud- N secuencia de vagones, donde N < K?
2. Considera el caso especial donde K = 4. Encuentra el DFT inverso del producto de los DFT de dos vagones de longitud 3.
3. Si pudiéramos usar DFT para realizar filtrado lineal, debería ser cierto que el producto de la DFT de entrada y la DFT de la respuesta de muestra unitaria es igual a la DFT de la salida. Para que puedas usar lo que acabas de calcular, deja que la entrada sea una señal de vagón y la respuesta unidad-muestra también sea un vagón. El resultado de la parte (b) sería entonces la salida del filtro si pudiéramos implementar el filtro con DFT de longitud 4. ¿La salida real del filtro boxcar-es igual al resultado encontrado en la parte anterior?
4. ¿Qué necesitaría cambiar para que el producto de los DFT de la respuesta de entrada y unidad-muestra en este caso igualara el DFT de la salida filtrada?

Trucos DSP

Sammy se enfrenta a la computación de lotes de transformadas discretas de Fourier. Él, por supuesto, utilizará el algoritmo FFT, pero está atrasado y necesita obtener sus resultados lo más rápido posible. Se le da la idea de computar dos transformaciones a la vez calculando la transformada de\[s(n)=s_{1}(n)+is_{2}(n) \nonumber \] donde s ₁ (n) y s ₂ (n) son dos señales de valor real de las que necesita para calcular los espectros. El problema es si puede recuperar las DFT individuales del resultado o no.

1. ¿Cuál será la DFT S (k) de esta señal de valor complejo en términos de _S1 (k) y _S2 (k), las DFT de las señales originales?
2. El amigo de Sammy, un Aggie que conoce algún procesamiento de señal, dice que recuperar los DFT deseados es fácil: “Solo encuentra las partes reales e imaginarias de S (k)”. Demostrar que este enfoque es demasiado simplista.
3. Si bien la idea de su amigo no es correcta, sí le da una idea. ¿Qué enfoque funcionará? Sugerencia: Utilice las propiedades de simetría de la DFT.
4. ¿Cómo cambia el número de cómputos con este enfoque? ¿La idea de Sammy conducirá finalmente a un cálculo más rápido de los DFT requeridos?

Transformada discreta de coseno (DCT)

La transformada discreta de coseno de una secuencia de longitud N se define como

\[S_{c}(k)=\sum_{n=0}^{N-1}s(n)\cos \left ( \frac{2\pi nk}{2N} \right ) \nonumber \]

Tenga en cuenta que el número de términos de frecuencia es\[2N-1:k=\left \{ 0,...,2N-1 \right \} \nonumber \]

1. Encuentra el DCT inverso.
2. ¿Se sostiene un teorema de Parseval para el DCT?
3. Usted elige transmitir información sobre la señal s (n) de acuerdo con los coeficientes DCT. Solo podrías enviar uno, ¿cuál enviarías?

Un filtro digital

Un filtro digital se describe mediante la siguiente ecuación de diferencia:

\[y(n)=ay(n-1)+ax(n)-x(n-1),a=\frac{1}{\sqrt{2}} \nonumber \]

1. ¿Cuál es la respuesta de muestra unitaria de este filtro?
2. ¿Cuál es la función de transferencia de este filtro?
3. ¿Cuál es la salida de este filtro cuando la entrada es\[\sin \left ( \frac{\pi n}{4} \right ) \nonumber \]

Otro filtro digital

Un filtro digital está determinado por la siguiente ecuación de diferencia.

\[y(n)=y(n-1)+x(n)-x(n-4) \nonumber \]

1. Encuentra la respuesta de muestra unitaria de este filtro.
2. ¿Cuál es la función de transferencia del filtro? ¿Cómo caracterizarías este filtro (paso bajo, paso alto, propósito especial,...)?
3. Encuentra la salida del filtro cuando la entrada es la sinusoide\[\sin \left ( \frac{\pi n}{2} \right ) \nonumber \]
4. En otro caso, la secuencia de entrada es cero para n < 0, luego se convierte en distinta de cero. Sammy mide la salida para ser\[y(n)=\delta (n)+\delta (n-1) \nonumber \] ¿Puede su medición ser correcta? En otras palabras, ¿hay algún insumo que pueda arrojar esta salida? Si es así, encuentra la entrada x (n) que da lugar a esta salida. Si no, ¿por qué no?

Otro filtro digital

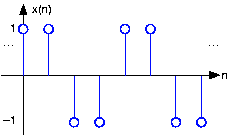
Un filtro tiene una relación entrada-salida dada por la ecuación de diferencia

\[y(n)=\frac{1}{4}x(n)+\frac{1}{2}x(n-1)+\frac{1}{4}x(n-2) \nonumber \]

1. ¿Cuál es la función de transferencia del filtro? ¿Cómo lo caracterizarías?
2. ¿Cuál es la salida del filtro cuando la entrada es igual a\[\cos \left ( \frac{\pi n}{2} \right ) \nonumber \]
3. ¿Cuál es la salida del filtro cuando la entrada es la onda cuadrada de tiempo discreto representada a continuación?

Figura 5.17.8

Un filtro digital en el dominio de la frecuencia

Tenemos un filtro con la función de transferencia

\[H(e^{i2\pi f})=e^{-(i2\pi f)}\cos (2\pi f) \nonumber \]

funcionamiento en la señal de entrada

\[x(n)=\delta (n)-\delta (n-2) \nonumber \]

que produce la salida y (n).

1. ¿Cuál es la respuesta unidad-muestra del filtro?
2. ¿Qué es la transformada discreta de Fourier de la salida?
3. ¿Cuál es la expresión de dominio de tiempo para la salida?

Filtros Digitales

Un sistema de tiempo discreto se rige por la ecuación de diferencia

\[y(n)=y(n-1)+\frac{x(n)+x(n-1)}{2} \nonumber \]

1. Encuentra la función de transferencia para este sistema.
2. ¿Cuál es la salida de este sistema cuando la entrada es\[\sin \left ( \frac{\pi n}{2}\right ) \nonumber \]
3. Si se observa que la salida es\[y(n)=\delta (n)+\delta (n-1) \nonumber \] entonces ¿cuál es la entrada?

Filtración Digital

Un filtro digital tiene una relación entrada-salida expresada por la ecuación de diferencia

\[y(n)=\frac{x(n)+x(n-1)+x(n-2)+x(n-3)}{4} \nonumber \]

1. Trazar la magnitud y fase de la función de transferencia de este filtro.
2. ¿Cuál es la salida de este filtro cuando\[x(n)=cos \left ( \frac{\pi n}{2}\right )+2sin \left ( \frac{2\pi n}{3}\right ) \nonumber \]

Trabajo Detective

1. La señal\[x(n)=\delta (n)-\delta (n-1) \nonumber \]
   1. Encuentra la longitud 8 DFT (transformada discreta de Fourier) de esta señal.
   2. Se le dice que cuando x (n) sirvió como entrada a un filtro lineal FIR (respuesta de impulso finito), la salida era\[y(n)=\delta (n)-\delta (n-1)+2\delta (n-2) \nonumber \] ¿Es verdadera esta afirmación? Si es así, indique por qué y encuentre la respuesta de muestra unitaria del sistema; si no, muestre por qué no.
2. Un sistema lineal de tiempo discreto, invariante de desplazamiento produce una salida\[y(n)=\left \{ 1,-1,0,0,... \right \} \nonumber \] cuando su entrada x (n) es igual a una muestra unitaria.
   1. Encuentra la ecuación de diferencia que rige el sistema.
   2. Encuentre la salida cuando\[x(n)=\cos (2\pi f_{0}n) \nonumber \]
   3. ¿Cómo describiría la función de este sistema?

La inversión de tiempo tiene usos

Un sistema de tiempo discreto tiene función de transferencia\[H(e^{i2\pi f}) \nonumber \] Una señal x (n) se pasa a través de este sistema para producir la señal w (n). La señal invertida en el tiempo w (-n) se pasa entonces a través del sistema para producir la salida invertida en el tiempo y (-n). ¿Cuál es la función de transferencia entre x (n) e y (n)?

Eliminación de “Hum”

La palabra argot “hum” representa formas de onda de línea eléctrica que se arrastran en señales debido a la mala construcción del circuito. Por lo general, la señal de 60 Hz (y sus armónicos) se agregan a la señal deseada. Lo que buscamos son filtros que puedan eliminar el zumbido. En este problema, se han muestreado la señal y el zumbido que lo acompaña; queremos diseñar un filtro digital para la eliminación de zumbidos.

1. Encuentre coeficientes de filtro para el filtro FIR de longitud 3 que pueden eliminar una sinusoide que tiene frecuencia digital f ₀ de su entrada.
2. Suponiendo que la frecuencia de muestreo es f _s a qué frecuencia analógica corresponde f ₀?
3. Un enfoque más general es diseñar un filtro que tenga una magnitud de respuesta de frecuencia proporcional al valor absoluto de un coseno:\[\left | H(e^{i2\pi f}) \right |\propto \left | \cos (\pi fN) \right | \nonumber \] De esta manera, no sólo se pueden eliminar los armónicos fundamentales sino también sus primeros armónicos. Seleccione el parámetro N y la frecuencia de muestreo para que las frecuencias a las que el coseno sea igual a cero correspondan a 60 Hz y sus armónicos impares hasta el quinto.
4. Encuentra la ecuación de diferencia que define este filtro.

Receptor digital AM

Pensando que las implementaciones digitales siempre son mejores, nuestro ingenioso ingeniero quiere diseñar un receptor AM digital. El receptor pasaría en banda la señal recibida, pasaría el resultado a través de un convertidor A/D, realizaría toda la demodulación con sistemas de procesamiento de señal digital y terminaría con un convertidor D/A para producir la señal de mensaje analógico. Supongamos en este problema que la frecuencia portadora es siempre un gran múltiplo incluso del ancho de banda W de la señal de mensaje.

1. ¿Cuál es la tasa de muestreo más pequeña que se necesitaría?
2. Mostrar el diagrama de bloques del receptor AM digital menos complejo.
3. Suponiendo que el canal agrega ruido blanco y que se usa un convertidor A/D de b bits, ¿cuál es la relación señal/ruido de la salida?

DFT

Un problema en la tarea de Samantha pide el DFT de 8 puntos de la señal de tiempo discreto\[\delta (n-1)+\delta (n-7) \nonumber \]

1. ¿Qué respuesta debe obtener Samantha?
2. Como cheque, su compañera de grupo Sammy dice que computó la DFT inversa de su respuesta y obtuvo\[\delta (n+1)+\delta (n-1) \nonumber \] ¿El resultado de Sammy significa que la respuesta de Samantha es incorrecta?
3. El problema de la tarea dice que se filtre la secuencia multiplicando su DFT por\[H(k)=\begin{cases} 1 & \text{ if }k=\left \{ 0,1,7 \right \} \\ 0 & \text{ if } otherwise \end{cases} \nonumber \] y luego calculando la DFT inversa. ¿Funcionará este algoritmo de filtrado? Si es así, encuentra la salida filtrada; si no, ¿por qué no?

Procesamiento de datos bursátiles

Debido a que una semana de negociación dura cinco días, los mercados de valores frecuentemente calculan promedios corrientes cada día durante los cinco días de negociación anteriores para suavizar las fluctuaciones de precios. El analista técnico de acciones de la firma de corretaje Buy-Lo-Sell-Hi ha escuchado que las técnicas de filtrado FFT funcionan mejor que cualquier otra (en términos de producir promedios más precisos).

1. ¿Cuál es la ecuación de diferencia que rige el promedio de cinco días para los precios diarios de las acciones?
2. Diseñe un algoritmo de filtrado eficiente basado en FFT para el corredor. ¿Cuántos datos deben procesarse a la vez para producir un algoritmo eficiente? ¿Qué transformada de longitud se debe usar?
3. ¿Es correcta la información del analista de que las técnicas FFT producen promedios más precisos que cualquier otra? ¿Por qué o por qué no?

Ecos

Los ecos no sólo ocurren en cañones, sino también en auditorios y circuitos telefónicos. En una situación en la que la señal de eco ha sido muestreada, la señal de entrada x (n) emerge como

\[x(n)+a_{1}x(n-n_{1})+a_{2}x(n-n_{2}) \nonumber \]

1. Encuentra la ecuación de diferencia del sistema que modela la producción de ecos.
2. Para simular este sistema de eco, se pide a los estudiantes ELEC 241 que escriban el programa más eficiente (más rápido) que tenga la misma relación insumo-producto. Supongamos que la duración de x (n) es 1,000 y que la\[a_{1}=\frac{1}{2},n_{1}=10,a_{2}=\frac{1}{5},n_{2}=25 \nonumber \] mitad de la clase vota para solo programar la ecuación de diferencia mientras que la otra mitad vota para programar un enfoque de dominio de frecuencia que explote la velocidad de la FFT. Por el voto indeciso, se debe romper el empate. ¿Qué enfoque es más eficiente y por qué?
3. Encuentra la función de transferencia y la ecuación de diferencia del sistema que suprime los ecos. En otras palabras, con la señal resonada como entrada, ¿qué salida del sistema es la señal x (n)?

Filtrado digital de señales analógicas

RU Electronics quiere desarrollar un filtro que se utilice en aplicaciones analógicas, pero que se implemente digitalmente. El filtro es para operar sobre señales que tienen un ancho de banda de 10 kHz, y servirá como filtro de paso bajo.

1. ¿Cuál es el diagrama de bloques para su implementación de filtros? Indicar explícitamente qué componentes son analógicos, cuáles son digitales (una computadora realiza la tarea), y qué interfaz entre los mundos analógico y digital.
2. ¿Qué frecuencia de muestreo se debe utilizar y cuántos bits se deben usar en el convertidor A/D para que la relación señal-ruido de la señal adquirida sea de al menos 60 dB? Para este cálculo, supongamos que la señal es una sinusoide.
3. Si el filtro es un filtro FIR de longitud 128 (la duración de la respuesta de muestra unitaria del filtro es igual a 128), ¿debería implementarse en el dominio de tiempo o frecuencia?
4. Suponiendo que\[H(e^{i2\pi f}) \nonumber \] es la función de transferencia del filtro digital, ¿cuál es la función de transferencia de su sistema?

Compresión de señal

Debido a la lentitud de Internet, la compresión de señal con pérdida se vuelve importante si desea que las señales se reciban rápidamente. Un estudiante emprendedor 241 ha propuesto un esquema basado en el procesamiento del dominio de la frecuencia. En primer lugar, seccionaría la señal en bloques de longitud- N, y computaría su DFT de N puntos. Luego descartaría (cero el espectro) a la mitad de las frecuencias, las cuantificaría a b -bits, y las enviaría a través de la red. El receptor ensamblaría el espectro transmitido y calcularía la DFT inversa, reconstituyendo así un bloque de N puntos.

1. ¿A qué frecuencias se debe poner a cero el espectro para minimizar el error en este esquema de compresión con pérdida?
2. La forma nominal de representar una señal digitalmente es usar una cuantificación simple de b bits de la forma de onda en el dominio del tiempo. ¿Cuánto tiempo debe estar una sección en el esquema propuesto para que el número requerido de bits/muestra sea menor que el requerido nominalmente?
3. Suponiendo que se pueda lograr una compresión efectiva, ¿el esquema propuesto arrojaría resultados satisfactorios?