9.2: Modelos de Inventario Tradicionales

Última actualización
Guardar como PDF

Page ID: 81002

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

9.2.1 Trading off Número de Configuraciones (Órdenes) para Inventario

Considera la siguiente situación, comúnmente llamada problema de cantidad de orden económico. Un producto se produce (o compra) para inventariar periódicamente. La demanda del producto se satisface a partir del inventario y es determinista y constante en el tiempo. ¿Cuántas unidades del producto deben producirse (o comprarse) a la vez para minimizar el costo anual, asumiendo que toda la demanda debe satisfacerse a tiempo? Este número de unidades se llama tamaño de lote.

El análisis podría proceder en las siguientes líneas.

¿Qué costos son relevantes?
1. El costo de producción (o compra) de cada unidad del producto se hunde, eso es lo mismo sin importar cuántas se hagan a la vez.
2. Hay un costo fijo por tirada de producción (o compra) sin importar cuántos se hagan.
3. Existe un costo de mantener una unidad de producto en inventario hasta que se venda, expresado en $/año.
  Tener una unidad en inventario es análogo a pedir dinero prestado. Se incurre en un gasto para producir el producto. Este gasto no puede ser reembolsado hasta que se venda el producto. Hay un “cargo por intereses” sobre el gasto hasta que se reembolsa. Esto es lo mismo que el costo de retención. Por lo tanto, el costo anual de tenencia por unidad a menudo se calcula como la tasa mínima atractiva de la compañía de retorno por el costo de una unidad del producto.
¿Qué supuestos se hacen?
1. La producción es instantánea. Esto puede o no ser una mala suposición. Si el producto se retira del inventario una vez al día y el inventario se puede reponer mediante una serie de producción programada de duración un día cada semana o dos, esta suposición está bien. Si las tiradas de producción no se pueden programar con precisión en el tiempo debido a limitaciones de capacidad o la competencia por los recursos de producción con otros productos o las series de producción tardan varios días, esta suposición puede hacer que los resultados obtenidos del modelo sean cuestionables.
2. Al finalizar la producción, el producto se puede colocar en inventario para su entrega inmediata a los clientes.
3. Cada ciclo de producción incurre en el mismo costo fijo de configuración, independientemente del tamaño o de las actividades competidoras en la planta de producción.
4. No hay competencia entre los productos por los recursos de producción. Si la planta de producción tiene capacidad suficiente, esta puede ser una suposición razonable. Si no, la producción puede no ocurrir exactamente en el momento necesario.

Las definiciones de todos los símbolos utilizados en el modelo de cantidad de orden económico (EOQ) se dan en el Cuadro 9-1.

Cuadro 9-1: Definición de símbolos para el modelo de cantidad de orden económico
Término	Definición
Tasa de demanda anual (D)	Unidades demandadas por año
Costo unitario de producción (c)	Costo de producción por unidad
Costo fijo por lote (A)	Costo de configuración para producir o comprar un lote
Costo de inventario por unidad por año (h)	h = i * c donde i es la tasa de interés corporativa
Tamaño del lote (Q)	Valor óptimo calculado utilizando el modelo de inventario
Pedidos por año (F)	D/Q
Tiempo entre órdenes	1/F = Q/D
Costo por año	Costo de configuración de ejecución (pedido) + costo de inventario = A * F + h * Q/2

Los componentes de costos del modelo son el costo de inventario anual y el costo anual de configuración de series de producción. El costo de inventario anual es el número promedio de unidades en inventario multiplicado por el costo de inventario por unidad por año. Dado que la demanda es constante, el inventario disminuye a una tasa constante desde su nivel máximo, el tamaño del lote Q, a 0. Así, el nivel promedio de inventario es simplemente Q/2. Esta idea se muestra en la Figura 9-1.

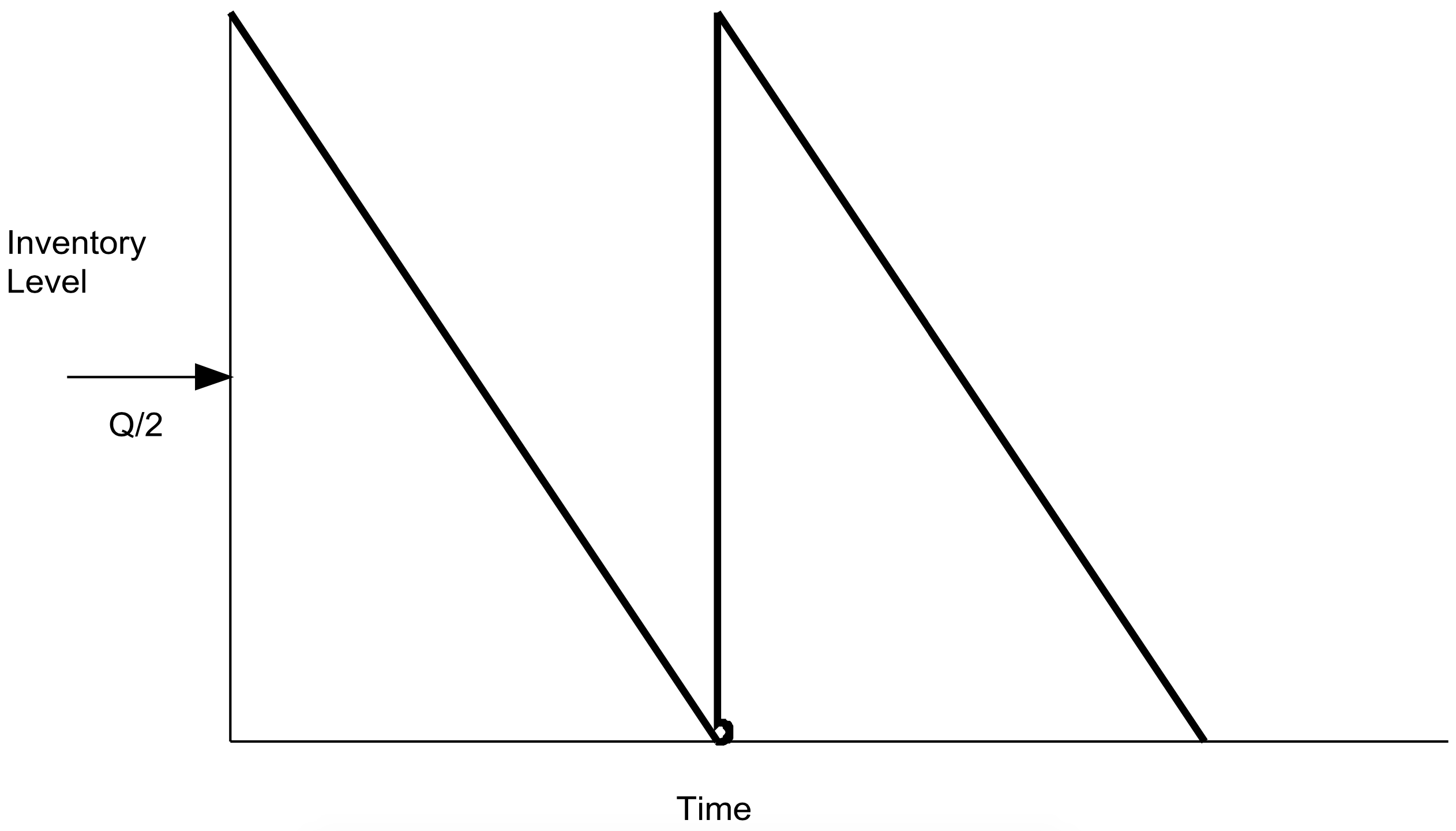
Screen Shot 2020-05-20 at 2.59.05 PM.png

El número de series de producción (pedidos) por año es la demanda dividida por el tamaño del lote. Así, el costo total por año viene dado por la ecuación 9-1.

\ begin {align} Y (Q) =h *\ frac {Q} {2} +A *\ frac {D} {Q}\ tag {9-1}\ end {align}

Encontrar el valor óptimo de Q se logra tomando la derivada con respecto a Q, poniéndola igual a 0 y resolviendo para Q. Esto arroja la ecuación 9-2.

\ begin {align} Q^ {*} =\ sqrt {\ frac {2 * A * D} {h}} =\ sqrt {\ frac {A} {h}} *\ sqrt {2 * D}\ tag {9-2}\ end {align}

Observe que el tamaño óptimo del lote Q depende de la raíz cuadrada de la relación entre el costo fijo por lote, A, y el costo de mantenimiento de inventario, h. Así, el costo de un lote se intercambia con el costo de mantenimiento de inventario para determinar el tamaño del lote.

Otras cantidades de interés son el número de pedidos por año (F) y el tiempo entre pedidos (T).

\ begin {align} F^ {*} =D/Q^ {*}\ tag {9-3}\ end {align}

\ begin {align} T^ {*} =1/F^ {*} =Q^ {*}/D\ tag {9-4}\ end {align}

Es importante señalar que:

Los modelos matemáticos ayudan a revelar las compensaciones entre los componentes o parámetros del sistema que compiten y ayudan a resolverlos.

Incluso si los valores no están disponibles para todos los parámetros del modelo, los modelos matemáticos son valiosos porque dan una idea de la naturaleza de las compensaciones. Por ejemplo en la ecuación 9- 2, a medida que el costo de mantenimiento aumenta el tamaño del lote disminuye y se hacen más pedidos por año. Esto tiene sentido, ya que un incremento en el costo de inventario por unidad debería llevar a un inventario promedio menor.

A medida que aumenta el costo fijo por lote, el tamaño del lote aumenta y se realizan menos pedidos por año. Esto tiene sentido ya que un aumento en el costo fijo costo por lote da como resultado menos lotes.

Supongamos que la información de costos es desconocida y no puede determinarse. ¿Qué se puede hacer en esta aplicación? Un enfoque es construir una gráfica del nivel promedio de inventario versus el número de series de producción (pedidos) por año. En la Figura 9-2 se muestra un gráfico de ejemplo. El punto de equilibrio óptimo está en el “codo” de la curva. A la derecha del codo, aumentar el número de tiradas de producción (pedidos) hace poco para bajar el inventario promedio. A la izquierda del codo, aumentar el inventario promedio hace poco para reducir el número de tiradas de producción (pedidos).

En la Figura 9-2, un inventario promedio de alrededor de 20 a 40 unidades conduce a alrededor de 40 a 75 series de producción al año. Esto sugiere que el tamaño óptimo del lote se puede cambiar dentro de un rango razonablemente amplio sin cambiar mucho el costo óptimo. Esto puede ser muy importante ya que los tamaños de los lotes pueden ser para fines prácticos restringidos a un cierto conjunto de valores, como múltiplos de 12, ya que la colocación de pedidos podría restringirse a semanal o mensual.

Ejemplo. Realizar un análisis de inventario versus tamaño de lote en la siguiente situación. La demanda de racks médicos es de 4000 racks por año. El costo de producción de un solo rack es de 250 dólares con un costo de configuración de ejecución de producción de $500. La tasa de retorno utilizada por la empresa es del 20%. Las series de producción se pueden realizar una vez por semana, una vez cada dos semanas o una vez cada cuatro semanas.

El tamaño óptimo del lote (número de unidades por ciclo de producción) viene dado por la ecuación 9-2:

$\ Q^{*}=\sqrt{\frac{2 * A * D}{h}}=\sqrt{\frac{2 * 500 * 4000}{250 * 20 \%}}=283$

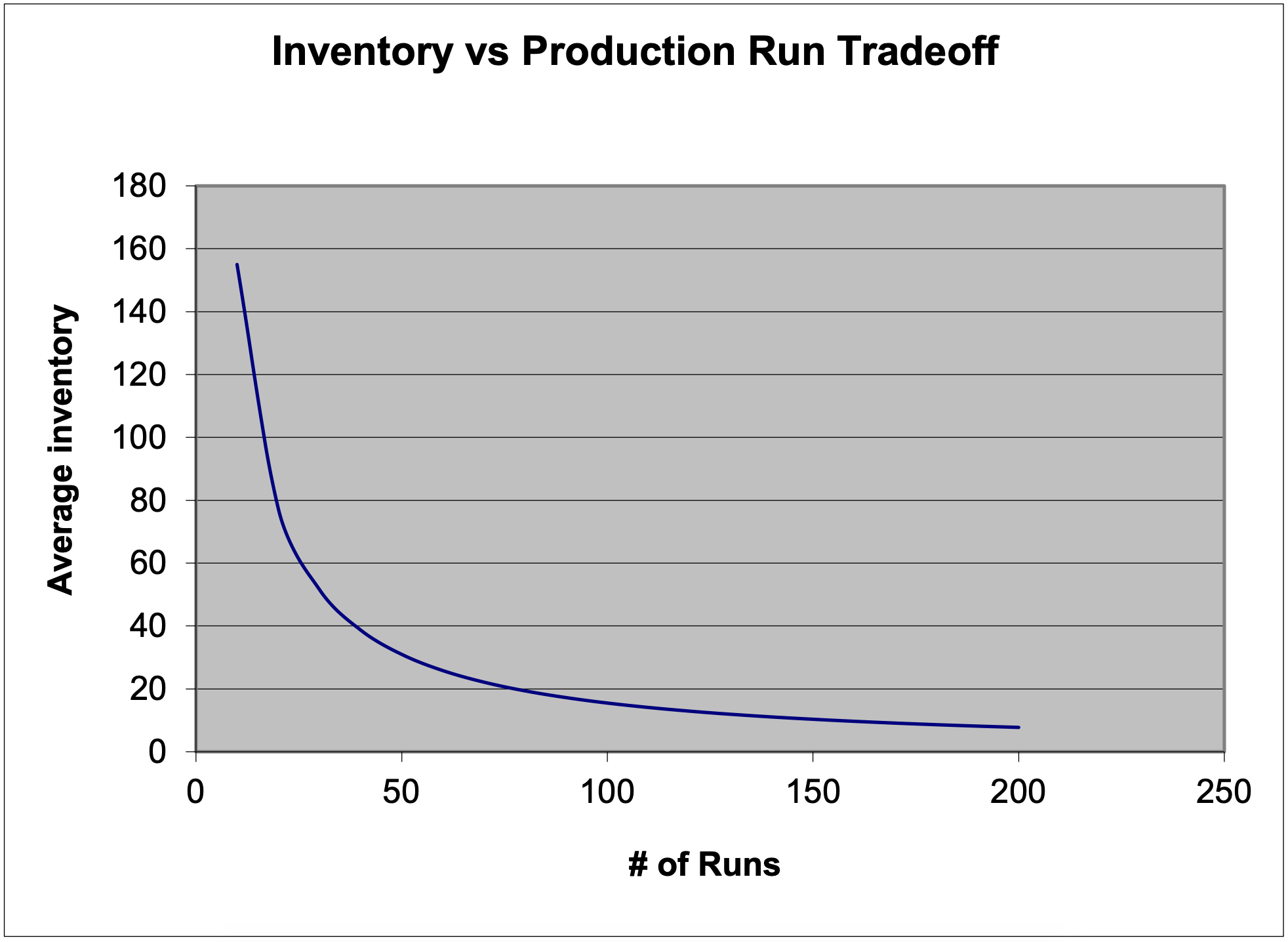
Screen Shot 2020-05-20 at 3.17.57 PM.png

El número de series de producción por año y el tiempo entre series de producción viene dado por las ecuaciones 9-3 y 4:

$\ F^{*}=D / Q^{*}=14.1$

$\ T^{*}=1 / F^{*}=Q^{*} / D=3.7 \text { weeks }$

El costo óptimo viene dado por la ecuación 9-1:

$\ Y\left(Q^{*}\right)=h * \frac{Q^{*}}{2}+A * \frac{D}{Q^{*}}=250 * 20 \% * \frac{283}{2}+500 * 14.1=7075+7071=14146$

La aplicación de la restricción en el tiempo entre series de producción produce lo siguiente.

$\ T^{\prime}=4\ weeks$

$\ F^{\prime}=52\ weeks\ /\ 4\ weeks =13$

$\ Q^{\prime}=4000 \ /\ F^{\prime}=308$

$\ Y\left(Q^{\prime}\right)=h * \frac{Q^{\prime}}{2}+A * \frac{D}{Q^{\prime}}=250 * 20 \% * \frac{308}{2}+500 * 13=7700+6500=14200$

Tenga en cuenta que cuando se usa el valor óptimo de Q, el costo de inventario y el costo de configuración de las series de producción son aproximadamente iguales. Cuando se usa el valor restringido, el costo de inventario aumenta ya que los tamaños de los lotes son más grandes pero el costo de configuración disminuye ya que se realizan menos tiradas de producción. El costo total es aproximadamente el mismo.

9.2.2 Nivel de Servicio al Cliente de Trading Off para Inventario

Idealmente, no sería necesario ningún inventario. Los bienes se producirían a pedido del cliente y se entregarían al cliente de manera oportuna. Sin embargo, esto no siempre es posible. Wendy's cocina tu hamburguesa a pedido pero un árbol de Navidad no se puede cultivar al tamaño exacto requerido mientras el cliente espera en el lote. Además, cuántos artículos demandan los clientes y cuándo ocurrirán estas demandas no se conoce de antemano y está sujeto a variación

Mantener el inventario ayuda a satisfacer la demanda de los clientes a tiempo a la luz de las condiciones descritas en el párrafo anterior. El nivel de servicio se define como el porcentaje de la demanda del cliente que se satisface a tiempo.

Considera el problema de decidir cuántos árboles de Navidad comprar para un lote de árboles de Navidad. Solo se puede realizar un pedido. Los árboles pueden ser entregados antes de que el lote abra al negocio. ¿Cuántos árboles de Navidad se deben ordenar si la demanda es una variable aleatoria distribuida normalmente con media y desviación estándar conocidas?

Hay una compensación entre:

Tener árboles sin vender que ni siquiera son buenos para la leña.
No tener árboles para vender a un cliente que habría comprado un árbol con una ganancia para el lote.

Las cantidades relevantes se definen en el Cuadro 9-2.

Tabla 9-2: Definición de símbolos para modelos de compensación de nivel de servicio — Inventario
Término	Definición
c _s	Costo de un stock out, por ejemplo no tener un árbol de navidad cuando un cliente quiere uno.
c _o	Costo de un excedente, por ejemplo haber sobrado árboles de Navidad
SL	Nivel de servicio
Q	Tamaño del lote o número de unidades a ordenar
$\ \mu$	Demanda media
$\ \sigma$	Desviación estándar de la demanda
z _p	Punto porcentual de la distribución normal estándar: P (Z$\ \leq$ z _p) = p. En Excel esto viene dado por NORMSINV (p)

Entonces se puede demostrar que se mantiene la siguiente ecuación:

\ begin {align} S L=\ frac {c_ {s}} {c_ {s} +c_ {o}} =\ frac {1} {1+c_ {o}/c_ {s}}\ tag {9-5}\ end {align}

Esta ecuación establece que el nivel de servicio óptimo de costo depende de la relación entre el costo de un stock out y el costo de un excedente.

En el ejemplo del árbol de Navidad, el costo de un excedente es el costo de un árbol de Navidad. El costo de un stock out es el beneficio obtenido al vender un árbol. Supongamos que el costo del árbol de navidad para el lote es de $15 y el árbol se vende por $50 (ahí está el espíritu navideño para ti). Esto implica que el costo de un stock out es de $50 - $15 = $35. El nivel de servicio óptimo de costo viene dado por la ecuación 9-5.

$\ S L=\frac{c_{s}}{c_{s}+c_{o}}=\frac{35}{35+15}=70 \%$

Si la demanda se distribuye normalmente, el número óptimo de unidades a ordenar viene dado por la ecuación general:

\ begin {align} Q^ {*} =\ mu+\ sigma^ {*} z_ {S L}\ tag {9-6}\ end {align}

Así, el número óptimo de árboles de Navidad a comprar si la demanda se distribuye normalmente con media 100 y desviación estándar 20 es

$\ Q^{*}=100+20 * z_{0.70}=100+20 * 0.524=111$

Existen numerosas situaciones similares a las que se puede aplicar la misma lógica. Por ejemplo, considere una tienda que venda un producto electrónico popular en particular. El producto se vuelve a suministrar periódicamente a través de un camión de reparto.

En esta aplicación, el costo excedente es igual al costo de mantenimiento de inventario que se puede calcular a partir del costo del producto y la tasa de interés de la empresa como se hizo en el modelo EOQ. El costo de desabasto podría calcularse como el beneficio unitario en la venta del producto.

No obstante, el gerente de la tienda siente que si el producto está agotado, el cliente puede ir a otra parte para todas sus necesidades de compra y nunca volver. Por lo tanto, se requiere un nivel de servicio preespecificado, generalmente en el rango de 90% a 99%. ¿Cuál es el costo de escasez implícito? Esto viene dado en términos generales por la ecuación 9- 7.

\ begin {align} c_ {s} =c_ {o} *\ frac {S L} {1-S L}\ tag {9-7}\ end {align}

Observe que esta es la ecuación es altamente no lineal con respecto al nivel de servicio.

Supongamos que las entregas se realizan semanalmente, el costo excedente (costo de mantenimiento de inventario) es de $1 por semana, y que un gerente especifica que el nivel de servicio sea del 90%. ¿Cuál es el costo implícito de un stock out? A partir de la ecuación 9- 7, este costo se calcula de la siguiente manera:

$\ c_{s}=c_{o} * \frac{S L}{1-S L}=\$ 1 * \frac{90 \%}{1-90 \%}=\$ 9$

Tenga en cuenta que si el nivel de servicio es del 99%, el costo de un stock out es de $99.