7.2: Ecuaciones diferenciales de primer orden
- Page ID
- 85391
Introducción
Consideramos la ecuación diferencial general de primer orden:
\[\tau \dfrac{d y(t)}{d t}+y(t)=x(t) \nonumber \]
La solución general viene dada por:
\[y(t)=y_{0} e^{-\left(t-t_{0}\right) / \tau}+\dfrac{e^{-\left(t-t_{0}\right) / \tau}}{\tau} \int_{t_{0}}^{t} x\left(t^{\prime}\right) e^{\left(t^{\prime}-t_{0}\right) / \tau} d t^{\prime} \nonumber \]
donde\(y_{0}=y \left(t-t_{0}\right)\). Tenga en cuenta que\(t^{\prime}\) se utiliza para distinguirse del límite superior\(t\) de la integral.
Para obtener la solución general, comience con la ecuación diferencial de primer orden:
\[\tau \dfrac{d y(t)}{d t}+y(t)=x(t) \nonumber \]
Divide ambos lados por\(\tau\):
\[\dfrac{d y(t)}{d t}+\dfrac{1}{\tau} y(t)=\dfrac{1}{\tau} x(t) \nonumber \]
Reescribe el LHS en forma condensada usando el factor de integración\(e^{ − t / τ}\):
\[e^{-t / \tau} \dfrac{d}{d t}\left[e^{t / \tau} y(t)\right]=\dfrac{1}{\tau} x(t) \nonumber \]
Observe cómo una diferenciación de cadena devolverá el LHS al formulario anterior
Simplificar:
\[\dfrac{d}{d t}\left[e^{t / \tau} y(t)\right]=\dfrac{1}{\tau} x(t) e^{t / \tau} \nonumber \]
Integrar ambos lados:
\[e^{t / \tau} y(t)-e^{t_{0} / \tau} y\left(t_{0}\right)=\dfrac{1}{\tau} \int_{t_{0}}^{t} x\left(t^{\prime}\right) e^{t^{\prime} / \tau} d t^{\prime} \nonumber \]
Resolver para\(y(t)\):
\[y(t)=y_{0} e^{-\left(t-t_{0}\right) / \tau}+\dfrac{e^{-t / \tau}}{\tau} \int_{t_{0}}^{t} x\left(t^{\prime}\right) e^{t^{\prime} / \tau} d t^{\prime} \nonumber \]
Considerar:
\[\dfrac{d y(t)}{d t}=x(t) \nonumber \]
Multiplicando ambos lados por\(dt\) da:
\[\int_{t_{0}}^{t} \dfrac{d y d t}{d t}=\int_{t_{0}}^{t} x\left(t^{\prime}\right) d t^{\prime} \nonumber \]
La solución general se da como:
\[y(t)=y_{0}+\int_{t_{0}}^{t} x\left(t^{\prime}\right) d t^{\prime} \nonumber \]
Ahora considere:
\[\dfrac{d y(t)}{d t}=-a y(t) \nonumber \]
Dividiendo ambos lados por\(y(t)\) da:
\[\dfrac{1}{y(t)} \dfrac{d y(t)}{d t}=-a \nonumber \]
que se puede reescribir como:
\[\dfrac{d}{d t}[\ln (y(t))]=-a \nonumber \]
Multiplicar ambos lados por\(dt\), integrar y establecer ambos lados de la ecuación como exponentes a la función exponencial da la solución general:
\[y(t)=y_{0} e^{-a\left(t-t_{0}\right)} \nonumber \]
Ahora considere:
\[\dfrac{d y(t)}{d t}=-a y(t)+x(t) \nonumber \]
Los pasos detallados de la solución son los siguientes:
1. Separar\(y(t)\) y\(x(t)\) términos
\[\dfrac{d y(t)}{d t}+a y(t)=x(t) \nonumber \]
2. Reescribir el LHS en forma condensada usando el “factor integrador”\(e^{ − at}\)
\[e^{-a t} \dfrac{d\left(e^{a t} y(t)\right)}{d t}=x(t) \nonumber \]
Observe cómo una diferenciación en cadena devolverá el LHS al formulario escrito en el paso 1
3. Divide ambos lados por\(e^{− at}\)
\[\dfrac{d\left(e^{a t} y(t)\right)}{d t}=e^{a t} x(t) \nonumber \]
4. Multiplicar ambos lados por\(dt\) e integrar
\[e^{a t} y(t)-e^{a t_{0}} y_{0}=\int_{t_{0}}^{t} x\left(t^{\prime}\right) e^{a t^{\prime}} d t^{\prime} \nonumber \]
La solución general se da como:
\[y(t)=y_{0} e^{-a\left(t-t_{0}\right)}+e^{-a t} \int_{t_{0}}^{t} x\left(t^{\prime}\right) e^{a\left(t^{\prime}-t_{0}\right)} d t^{\prime} \nonumber \]
Simplificación de la función escalonada
\[\tau \dfrac{d y(t)}{d t}+y(t)=x(t) \nonumber \]
Para\(x(t)=\Theta\left(t-t_{0}\right)\), que es la función de paso y\(y_{0}=0\)
Es decir,\(x(t)=1\) para\( t_0 > t_o\) y de\(x(t)=0\) otra manera:
La solución general previamente derivada:
\[y(t)=y_{0} e^{-\left(t-t_{0}\right) / \tau}+\dfrac{e^{-\left(t-t_{0}\right) / \tau}}{\tau} \int_{t_{0}}^{t} x\left(t^{\prime}\right) e^{\left(t^{\prime}-t_{0}\right) / \tau} d t^{\prime} \nonumber \]
reduce a:
\[y(t)=e^{-\left(t-t_{0}\right) / \tau} \nonumber \]
ya que la integral es igual a 1.
\(tau\)Se puede ver que la cantidad es la constante de tiempo por la cual\(y(t)\) cae a\(1/e\) su valor original
Considerar la ecuación diferencial
\[\dfrac{d y(t)}{d t}=-0.5 y(t)+x(t) \nonumber \]
donde\(x(t)=2+0.01 t\)
Asumiendo\(y_o =0\), ¿cuál es el comportamiento de\(y(t)\)?
Solución
La solución general se derivó previamente como:
\[y(t)=y_{0} e^{-a\left(t-t_{0}\right)}+e^{-a t} \int_{t_{0}}^{t} x\left(t^{\prime}\right) e^{a\left(t^{\prime}-t_{0}\right)} d t^{\prime} \nonumber \]
Para\(a=0.5\) y\(y_o = 0\), mientras se establece\(t_o=0\), la solución se reduce a:
\[y(t)=e^{-0.5 t} \int_{0}^{t}\left(2+0.01 t^{\prime}\right) e^{0.5\left(t^{\prime}\right)} d t^{\prime} \nonumber \]
El siguiente enlace puede ser referido para tablas integrales: S.O.S. Math
Simplificar la solución da lo siguiente:
\[y(t)=\dfrac{\left.\left(e^{-0.5 t}\right)\left((x+198)\left(e^{0.5 t}\right)-198\right)\right)}{50} \nonumber \]
Al trazar esta función se muestra el siguiente comportamiento:
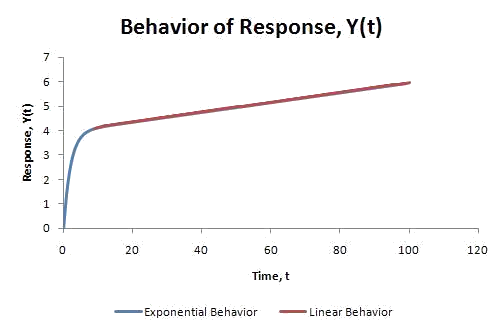
Como se puede apreciar claramente en la gráfica, inicialmente la respuesta sistémica muestra características más exponenciales. Sin embargo, a medida que avanza el tiempo, domina el comportamiento lineal.


