7.3: Ecuaciones diferenciales de segundo orden

Introducción

Consideramos la ecuación diferencial general de segundo orden:

\[\tau^{2} \frac{d^{2} Y(t)}{d t^{2}}+2 \zeta \tau \frac{d Y(t)}{d t} + Y(t)=X(t) \nonumber \]

Si expande la ecuación diferencial de segundo orden anterior:

\[ \begin{align*} \tau_{1} \tau_{2} \frac{d^{2} Y(t)}{d t^{2}}+\left(\tau_{1}+\tau_{2}\right) \frac{d Y(t)}{d t} + Y(t) &=X(t) \\[4pt] \left(\tau_{1} \frac{d}{d t}+1\right)\left(\tau_{2} \frac{d}{d t}+1\right) Y(t) &=X(t) \end{align*}  \nonumber \]

donde:

\[\tau=\sqrt{\tau_{1} \tau_{2}} \nonumber \]

\[\zeta=\frac{\tau_{1}+\tau_{2}}{2 \sqrt{\tau_{1} \tau_{2}}} \nonumber \]

La expansión de la ecuación diferencial permite adivinar cómo se verá la forma de la solución (\(Y(t)\)) cuando\(X(t)=1\).

Se aplican las siguientes reglas cuando\(τ_1 = Re(τ_1)+ i*Im(τ_1)\) y\(τ_2 = Re(τ_2)+ i*Im(τ_2)\):

• Si Re (τ ₁) y Re (τ ₂) son ambos positivos, y NO hay partes imaginarias,\(Y(t)\) desintegrarán exponencialmente (sobreamortiguado).
• Si Re (τ ₁) y Re (τ ₂) son ambos positivos, y hay partes imaginarias,\(Y(t)\) oscilarán hasta que alcance el estado estacionario (subamortiguado).
• Si Re (τ ₁) y Re (τ ₂) son ambos negativos, y NO hay partes imaginarias,\(Y(t)\) crecerán exponencialmente (inestable).
• Si Re (τ ₁) y Re (τ ₂) son ambos negativos, y hay partes imaginarias,\(Y(t)\) oscilarán y crecerán exponencialmente (inestable).
• Si Re (τ ₁) y Re (τ ₂) son ambos cero, y hay partes imaginarias,\(Y(t)\) oscilarán y no crecerán ni decairán.
• Si τ ₁ y τ ₂ son ambos cero,\(Y(t)\) es igual a X (t).

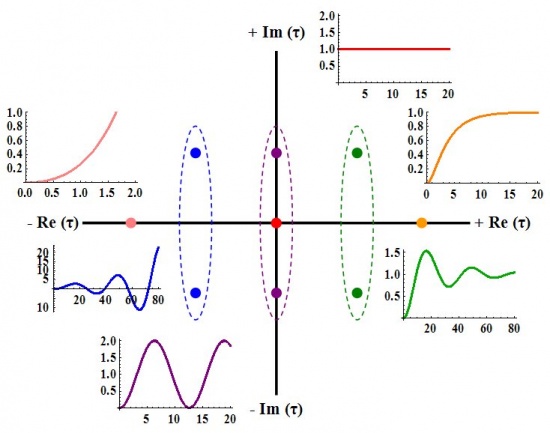
Solución del Sistema General de Segundo Orden (Cuando X (t) = θ (t))

La solución para la salida del sistema,\(Y(t)\), se puede encontrar en la siguiente sección, si asumimos que la entrada,\(X(t)\), es una función de paso\(θ(t)\). La solución dependerá del valor de. Si es menor que uno,\(Y(t)\) quedará subamortiguado. Esto significa que la salida se sobrepasará y oscilará. Si es igual a uno,\(Y(t)\) será amortiguado críticamente. Esto significa que la salida alcanzará el valor de estado estacionario rápidamente, sin sobreimpulso ni oscilación. Si es mayor que uno,\(Y(t)\) se sobrehumedecerá. Esto significa que la salida no alcanzará el valor de estado estacionario tan rápido como un sistema críticamente amortiguado, pero no habrá sobreimpulso u oscilación.

Subamortiguado (<1)

Si\(ζ < 1\), la solución es:

\[Y(t)=1-\frac{1}{\sqrt{1-\zeta^{2}}} e^{-\zeta t / \tau} \sin \left(\sqrt{1-\zeta^{2}} \frac{t}{\tau}+\phi\right) \nonumber \]

donde:

\[\phi=-\tan ^{-1}\left(\frac{\sqrt{1-\zeta^{2}}}{\zeta}\right) \nonumber \]

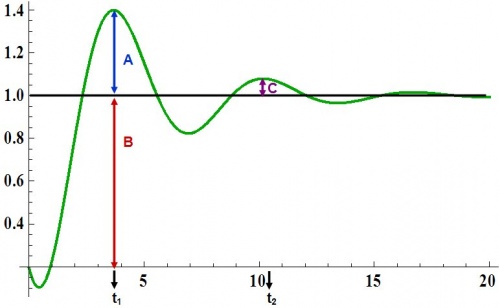
La relación de decaimiento (C/A) se puede calcular usando la siguiente ecuación:

\[\frac{C}{A}=e^{-2 \pi \zeta / \sqrt{1-\zeta^{2}}} \nonumber \]

El sobreimpulso (A/B) se puede calcular usando la siguiente ecuación:

\[\frac{A}{B}=e^{-\pi \zeta / \sqrt{1-\zeta^{2}}} \nonumber \]

El periodo (\(T\)) y la frecuencia (\(ω\)) son los siguientes:

\[T=t_{2}-t_{1}=\frac{2 \pi \tau}{\sqrt{1-\zeta^{2}}} \nonumber \]

\[\omega=\frac{2 \pi}{T}=\frac{\sqrt{1-\zeta^{2}}}{\tau} \nonumber \]

Amortiguado críticamente (=1)

Si\(ζ = 1\), la solución es:

\[Y(t)=1-\left(1+\frac{t}{\tau}\right) e^{-t / \tau} \nonumber \]

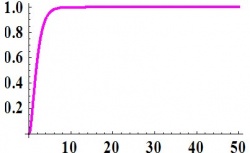
Sobreamortiguado (>1)

Si\(ζ > 1\), la solución es:

\[Y(t)=1-\frac{1}{\sqrt{\zeta^{2}-1}} e^{-\zeta t / \tau} \sinh \left(\sqrt{\zeta^{2}-1} \frac{t}{\tau}+\phi\right) \nonumber \]

donde:

\[\phi=-\tanh ^{-1}\left(\frac{\sqrt{\zeta^{2}-1}}{\zeta}\right) \nonumber \]

Ejemplo\(\PageIndex{1}\)

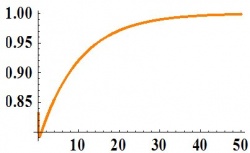
Dado:

• A ₁ = 1 m ²
• A ₂ = 1.5 m ²
• R ₁ = 0.25 s/ m ²
• R ₂ = 0.75 s/ m ²

donde:

• A es el área del tanque
• Q es el caudal volumétrico
• R es la resistencia al flujo de la corriente que sale del tanque
• H es la altura del líquido en el tanque

desarrollar una expresión que describa la respuesta de H ₂ a Q _en. Determine si el sistema está sobre, por debajo o críticamente amortiguado y determine cómo sería la gráfica de la expresión usando el plano complejo τ anterior. A continuación se muestra un diagrama del sistema:

Solución

Realización de un balance de masa en cada tanque:

\[A_{1} \frac{d H_{1}}{d t}=Q_{i n}-\frac{H_{1}}{R_{1}} \label{1} \]

\[A_{2} \frac{d H_{2}}{d t}=\frac{H_{1}}{R_{1}}-\frac{H_{2}}{R_{2}} \label{2} \]

donde los términos de la izquierda dan cuenta de la acumulación en el tanque y los términos de la derecha dan cuenta del flujo en los arroyos de entrada y salida

Dejar τ ₁ = R ₁ A ₁ y τ ₂ = R ₂ A ₂

Ecuaciones\ ref {1} y\ ref {2} ahora se convierten

\[\tau_{1} \frac{d H_{1}}{d t}=R_{1} Q_{i n}-H_{1} \label{3} \]

\[\tau_{2} \frac{d H_{2}}{d t}=\frac{R_{2}}{R_{1}} H_{1}-H_{2} \label{4} \]

Poner términos similares en el mismo lado y factor

\[\left(\tau_{1} \frac{d}{d t}+1\right) H_{1}=R_{1} Q_{i n} \label{5} \]

\[\left(\tau_{2} \frac{d}{d t}+1\right) H_{2}=\frac{R_{2}}{R_{1}} H_{1} \label{6} \]

Aplicar\(\left(\tau_{1} \frac{d}{d t}+1\right)\) operador de la ecuación\ ref {5} a la ecuación\ ref {6}

\[\left(\tau_{1} \frac{d}{d t}+1\right)\left(\tau_{2} \frac{d}{d t}+1\right) H_{2}=\left(\tau_{1} \frac{d}{d t}+1\right) \frac{R_{2}}{R_{1}} H_{1} \label{7} \]

El\(\left(\tau_{1} \frac{d}{d t}+1\right) H_{1}\) término de la porción izquierda de la Ecuación\ ref {5} se puede sustituir en el lado derecho de la Ecuación\ ref {7}

\[\left(\tau_{1} \frac{d}{d t}+1\right)\left(\tau_{2} \frac{d}{d t}+1\right) H_{2}=R_{1} Q_{i n} \frac{R_{2}}{R_{1}} \nonumber \]

\[\left(\tau_{1} \frac{d}{d t}+1\right)\left(\tau_{2} \frac{d}{d t}+1\right) H_{2}=Q_{i n} R_{2} \nonumber \]

_{Esta expresión muestra la respuesta de H 2 a Q como una solución de segundo orden como las que se muestran arriba.} Aquí Y (t) =H ₂ y X (t) =R ₂ Q _en

\[\zeta=\frac{\tau_{1}+\tau_{2}}{2 \sqrt{\tau_{1} \tau_{2}}}=\frac{(0.25 * 1)+(0.75 * 1.5)}{2 \sqrt{(0.25 * 1)(0.75 * 1.5)}}=1.296 \nonumber \]

Sobrehumedecido.

Ambos valores de\(τ\) son números reales positivos, y el comportamiento de la gráfica de la ecuación se puede encontrar en el plano complejo τ anterior.

Ejemplo\(\PageIndex{2}\): Analogy to Physics - Spring System

Podría ser útil usar un sistema de resorte como analogía para nuestros sistemas de segundo orden.

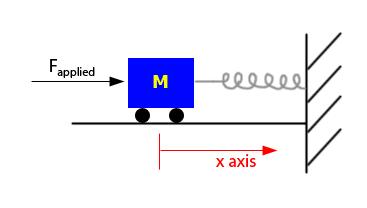
De la segunda ley de movimiento de Newton,

\[F = ma \nonumber \]

donde:

• \(F\)es Fuerza
• \(m\)es masa
• \(a\)es aceleración

Para el sistema de muelles, esta ecuación se puede escribir como:

\[F_{\text {applied}}-F_{\text {friction}}-F_{\text {restoring}}=m x^{\prime \prime} \nonumber \]

donde\(x'\) esta la aceleracion del carro en la dirección x

\[F_{\text {applied}}-f x-k x=m x^{\prime \prime} \nonumber \]

donde:

• k es la constante de resorte, que relaciona el desplazamiento del objeto con la fuerza aplicada
• f es la frecuencia de oscilación

\[\frac{m}{k} x^{\prime \prime}+\frac{f}{k} x^{\prime}+x=F_{a p p l i e d} \nonumber \]

Como puede ver, esta ecuación se asemeja a la forma de una ecuación de segundo orden. La ecuación puede entonces pensarse como:

\[\mathrm{T}^{2} X^{\prime \prime}+2 \zeta \mathrm{T} X^{\prime}+X=F_{\text {applied }} \nonumber \]

\[\tau=\sqrt{\frac{m}{k}} \nonumber \]

\[\zeta=\frac{f}{2 \sqrt{m k}} \nonumber \]

Debido a esto, el resorte exhibe un comportamiento como ecuaciones diferenciales de segundo orden:

• Si\(ζ > 1\) o\(f>2 \sqrt{m k}\) está sobreamortiguado
• Si\(ζ = 1\) o\(f = 2 \sqrt{m k}\) está amortiguado críticamente
• Si\(ζ < 1\) o\(f < 2 \sqrt{m k}\) está subamortiguado