9.4: Sintonización PID vía Respuestas de Frecuencia con Gráficas de Bode
- Page ID
- 85571
Descripción de la relación de amplitud, desplazamiento de fase y respuesta de frecuencia
Una buena manera de entender el significado físico de la relación de amplitud y el desplazamiento de fase y cómo cambian en función de la frecuencia del flujo de entrada es a través del análisis de un sistema simple. Un buen ejemplo es un reactor de tanque agitado continuo (CSTR) bien aislado con un flujo de entrada igual a su flujo de salida (Figura\(\PageIndex{1}\)). Para esta descripción consideramos la temperatura de entrada y salida, pero también se podría utilizar la concentración de entrada o la velocidad de alimentación.
Si el CSTR está inicialmente a 55˚C, y el flujo de entrada tiene una temperatura que fluctúa sinusoidalmente entre 50˚C y 60˚C, la temperatura de salida también variará sinusoidalmente. Si el fluido tiene un tiempo de residencia grande en el tanque, y la frecuencia de la variación de temperatura del fluido de entrada es alta en relación con el tiempo de residencia. Entonces la temperatura de salida también variará rápidamente de manera sinusoidal, pero con una amplitud significativamente menor que la de la entrada. La gran retención en el tanque bien mezclado amortigua las fluctuaciones en la temperatura de entrada. En contraste, si la frecuencia de la onda sinusoidal de temperatura de entrada es baja en relación con el tiempo de residencia del fluido, la salida también será una onda sinusoidal con temperaturas que oscilan entre los 50˚C y los 60˚C.
En ambos casos descritos anteriormente habrá un retraso o desplazamiento de fase entre la entrada y la salida del sistema (ver la figura inmediatamente a continuación). En nuestro ejemplo, el desplazamiento de fase está controlado por el tiempo promedio de residencia del fluido en el tanque. La constante de tiempo de este sistema es el tiempo promedio de residencia del tanque. Un sistema con un tiempo de residencia pequeño responderá muy rápidamente a los cambios en el caudal de entrada, y los tiempos de residencia grandes darán como resultado un tiempo de retraso considerable.
A medida que aumenta la frecuencia de la variación de temperatura, el periodo de la entrada disminuye y el desplazamiento de fase se hace mayor. Esto se puede ver en la Figura\(\PageIndex{2}\):
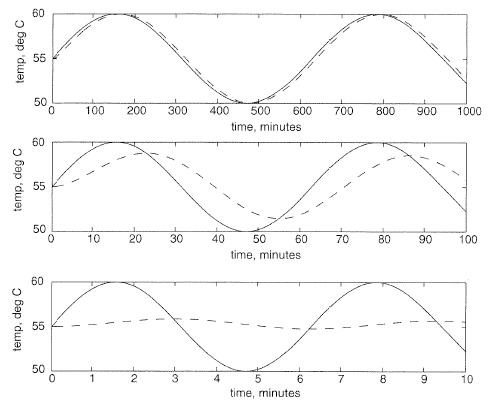
Imagínese que tenemos una reacción sensible que debe mantenerse con 3˚C de 55˚C, ahora se vuelve de suma importancia que entendamos la respuesta de frecuencia de este sistema CSTR. Aquí está la utilidad de las parcelas de Bode; representan un rango de diferentes respuestas de frecuencia en dos parcelas. Esto permite una determinación relativamente rápida de la robustez del sistema. Además, la respuesta de frecuencia y el análisis de gráficos Bode se pueden utilizar para ajustar los sistemas de control PID.
Respuesta de frecuencia
Para un proceso dado descrito por\(Y(t)=\hat{G} X(t)\), se considera una entrada sinusoidal
\[X(t)=\sin (\omega t)\nonumber \]
Después de mucho tiempo, la solución también será sinusoidal, con
\[Y(t) \sim A R \sin (\omega t+\phi)\nonumber \]
donde\(AR\) está la relación de amplitud (debe ser un número positivo) y\(\phi\) es el retraso de fase (\(\phi < 0\)) o el plomo de fase (\(\phi > 0\)).
A veces, para resolver el\(Y(t)\) uso de un solucionador de ODE, es útil tener la ecuación del proceso en la forma\(X(t)=\hat{G}^{-1} Y(t)\) y definir en\(\hat{G}^{-1}\) lugar de\(\hat{G}\).
Expresiones para AR y\(\phi\)
Sistema de primer orden
\[A R=\frac{1}{\sqrt{1+\omega^{2} \tau_{p}^{2}}}\nonumber \]
\[\phi=\tan ^{-1}\left(-\omega \tau_{p}\right)\nonumber \]
Sistema de segundo orden
\[A R=\frac{1}{\sqrt{\left(1-\omega^{2} \tau_{p}^{2}\right)^{2}+\left(2 \zeta \omega \tau_{p}\right)^{2}}}\nonumber \]
\[\phi=\tan ^{-1}\left(\frac{-2 \zeta_{p} \omega \tau_{p}}{1-\omega^{2} \tau_{p}^{2}}\right)\nonumber \]
Tiempo Muerto
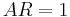
\ [A R=1]
\[\phi=-\omega \tau_{\text {dead}}\nonumber \]
Sistemas en serie
\[A R=A R_{1} \cdot A R_{2} \cdot \ldots\nonumber \]
\[\log A R=\log A R_{1}+\log A R_{2}+\ldots\nonumber \]
\[\phi=\phi_{1}+\phi_{2}+\ldots\nonumber \]
Controlador P
\[\hat{G}_{c}=K_{c}\nonumber \]
\[A R=K_{c}\nonumber \]
\[\phi=0\nonumber \]
Controlador PI
\[\hat{G}_{c}=K_{c}\left(1+\frac{1}{\tau_{I}} \int_{0}^{t} d t^{\prime}\right)\nonumber \]
\[\phi=\tan ^{-1}\left(-\frac{1}{\omega \tau_{I}}\right)\nonumber \]
Controlador PD
\[A R=K_{c} \sqrt{1+\omega^{2} \tau_{D}^{2}}\nonumber \]
\[\phi=\tan ^{-1}\left(\omega \tau_{D}\right)\nonumber \]
Controlador PID
\[\phi=\tan ^{-1}\left(\omega \tau_{D}-\frac{1}{\omega \tau_{I}}\right)\nonumber \]
Introducción a las parcelas de Bode
Debido a que es imposible modelar perfectamente un proceso químico real, los ingenieros de control están interesados en caracterizar la robustez del sistema, es decir, quieren ajustar los controladores para soportar un rango razonable de cambios en los parámetros del proceso mientras mantienen un sistema de retroalimentación estable. Las parcelas de Bode proporcionan un medio efectivo para cuantificar la estabilidad del sistema. Las gráficas de Bode describen un sistema de bucle abierto o cerrado en función de la frecuencia de entrada y dan una imagen de la estabilidad del sistema. Si todas las entradas a un sistema fueran constantes, sería una tarea relativamente sencilla controlar el sistema y su salida. Sin embargo, si un valor de entrada, como la temperatura, varía sinusoidalmente, entonces la salida también debería describirse como una función sinusoidal. En este caso, las gráficas Bode son una herramienta útil para predecir la respuesta del sistema. Hay dos parcelas de Bode utilizadas para describir un sistema. El primero muestra la relación de amplitud en función de la frecuencia. La relación de amplitud es la amplitud de la onda sinusoidal de salida dividida por la onda sinusoidal de entrada. La segunda gráfica grafica el desplazamiento de fase en función de la frecuencia, donde el desplazamiento de fase es el desfase de tiempo entre la salida y las curvas sinusoidales de entrada dividido por el periodo de cualquiera de las curvas sinusoidales y luego multiplicado por -360° (o\(-2π\) radianes) para expresar este desplazamiento como un ángulo.
Construyendo parcelas de Bode
Las gráficas de Bode muestran de manera concisa toda la información relevante de entrada y salida de frecuencia en dos gráficas: la relación de amplitud como función de la frecuencia y el desplazamiento de fase en función de la frecuencia. La gráfica de relación de amplitud es una gráfica log-log mientras que la gráfica de ángulo de fase es una gráfica semilog (o log-lineal).
Para construir una gráfica de Bode, un ingeniero tendría datos empíricos que mostraran valores de entrada y salida que varían como funciones sinusoidales del tiempo. Por ejemplo, puede haber datos de temperatura de entrada que varían sinusoidalmente y los datos de temperatura de salida que también varían sinusoidalmente. Por ejemplo, dado un intercambiador de calor que se utiliza para enfriar una corriente caliente, podemos variar el caudal de la corriente caliente y modelarla sinusodialmente. (Esto se puede hacer usando ODEs y un modelo Excel de un intercambiador de calor).
La figura\(\PageIndex{3}\) incluye el caudal de entrada (corriente de fluido de proceso) que varía como una función sinusoidal y la temperatura caliente que sale del intercambiador de calor variando igualmente como una función sinusoidal. Partes de esta gráfica aún no están en estado estacionario.
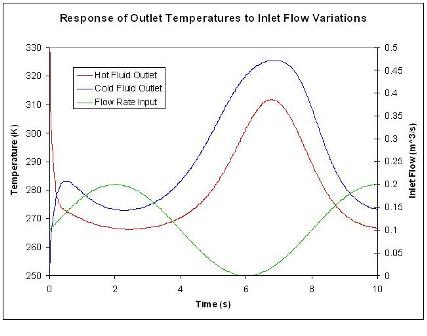
Las parcelas de Bode se construyen a partir de datos de estado estacionario. La figura\(\PageIndex{4}\) muestra parte de la región de estado estacionario de los mismos datos utilizados para la figura\(\PageIndex{3}\).
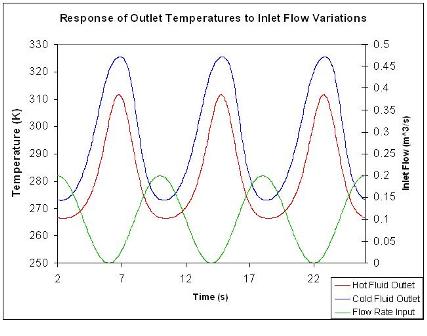
Para recopilar un solo punto de datos para una gráfica de Bode, utilizaremos la información de un solo período del caudal de entrada y la temperatura correspondiente de la corriente de salida caliente.
La relación de amplitud,\(AR\), es la relación de la amplitud de la curva sinusoidal de salida dividida por la amplitud de la curva sinusoidal de entrada.
\[A R=\dfrac{\text { output amplitude }}{\text {input amplitude}} \nonumber \nonumber \]
El valor de la relación de amplitud debe ser sin unidades por lo que si las unidades de la frecuencia de entrada y las unidades de la frecuencia de salida no son las mismas, primero se deben normalizar los datos de frecuencia. Por ejemplo, si la frecuencia de entrada está en ˚C/min y la frecuencia de salida también está en ˚C/min, entonces AR no tiene unidades y no necesita normalizarse. Si, en cambio, la frecuencia de entrada está en L/min y la frecuencia de salida está en ˚C/min, entonces AR = ˚C/litros. En este caso las frecuencias de entrada y salida necesitan normalizarse porque la relación AR = ˚C/L no dice nada sobre el significado físico del sistema. El valor de AR sería completamente diferente si las unidades de AR fueran Kelvin/gal.
Para encontrar el desplazamiento de fase, es necesario encontrar los periodos de las curvas sinusoidales de entrada y salida. Recordemos que el periodo\(P\),, es el periodo de tiempo de un pico al siguiente.
\[P=\frac{1}{f}=\frac{2 \pi}{\omega}\nonumber \]
con\(f\) es la frecuencia y\(\omega\) es la frecuencia angular (rad/seg)
El desplazamiento de fase se encuentra entonces por
\[\phi=-2 \pi \left(\dfrac{\Delta P}{P}\right)\nonumber \]
Usando estos valores encontrados a partir de múltiples perturbaciones en el caudal de alimentación, es posible construir las siguientes gráficas de Bode:
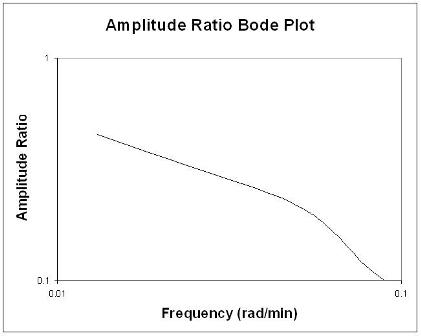
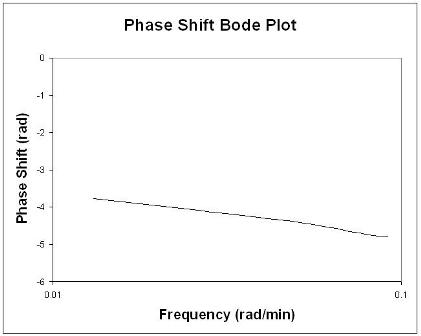
Reglas generales al analizar parcelas de Bode
En términos generales, un cambio de ganancia desplaza la relación de amplitud hacia arriba o hacia abajo, pero no afecta el ángulo de fase. Un cambio en el retardo de tiempo afecta el ángulo de fase, pero no la relación de amplitud. Por ejemplo, un aumento en el retardo de tiempo hace que el desplazamiento de fase sea más negativo para cualquier frecuencia dada. Un cambio en la constante de tiempo cambia tanto la relación de amplitud como el ángulo de fase. Por ejemplo, un aumento en la constante de tiempo disminuirá la relación de amplitud y hará que el retraso de fase sea más negativo en cualquier frecuencia dada.
| Cambiar | Efecto |
|---|---|
| Cambio de ganancia | La relación de amplitud se desplaza hacia arriba o hacia abajo; sin cambios en el ángulo de fase |
| Retraso de tiempo | Cambios de ángulo de fase, pero sin cambios en la relación de amplitud |
Antes de la llegada de potentes herramientas de modelado por computadora, los ingenieros de controles modelarían sistemas usando funciones de transferencia. Los lectores interesados en aprender más sobre cómo se utilizaron estos para construir parcelas de Bode deben referirse a Control de Procesos: Modelado, Diseño y Simulación de Bequette (ver Referencias). Este wiki asume que el ingeniero ya tiene datos en Excel, etc, que muestran el comportamiento sinusoidal de entrada y salidas.
Criterio de estabilidad de Bode
Un sistema de control es inestable si la respuesta de frecuencia de bucle abierto exhibe un AR que excede la unidad a la frecuencia para la cual el retardo de fase es de 180 grados. Esta frecuencia se llama la frecuencia de cruce. Ajustar la ganancia para que el AR < 1 para - phi < (180 menos margen de fase) resulte en una estabilidad aceptable si el margen de fase es mayor a 30 grados.
Como se mencionó anteriormente, el ingeniero de controles utiliza parcelas Bode para caracterizar la estabilidad del sistema. Si encontraras que la relación de amplitud es mayor a 1 el sistema sería inestable a esa frecuencia. Un criterio de estabilidad importante es que AR < 1 cuando el desplazamiento de fase = -180 grados (o -pi radianes). Esto se llama el criterio de estabilidad de Bode y si se mantiene para un sistema de bucle cerrado, entonces ese sistema será estable. Si no se cumple este criterio y se le pusiera un controlador de retroalimentación a este proceso, como se hizo en la sintonización PID vía optimización, el proceso explotaría debido al retraso de respuesta. La razón de esto es que el sistema podría pensar que la temperatura es demasiado baja cuando en realidad es demasiado alta, por lo que disminuiría el agua de refrigeración en lugar de aumentarla. Además, con un AR < 1, se amplifica un error en la entrada en la salida, por lo que el sistema perderá el control debido a la amplificación del error. Esto obviamente podría ser una situación peligrosa, por ejemplo en un CSTR exotérmico, que podría explotar.
Respuesta de frecuencia en Mathematica
Parcela de Bode para controlador PD, T5 D = 1:
AR = Sqrt [1 + omega^2]
phi = 180/pi*Arctan [omega]
LogLogPlot [AR, {omega,0.01,100}]
LoglinearPlot [phi, {omega,0.01,100}]
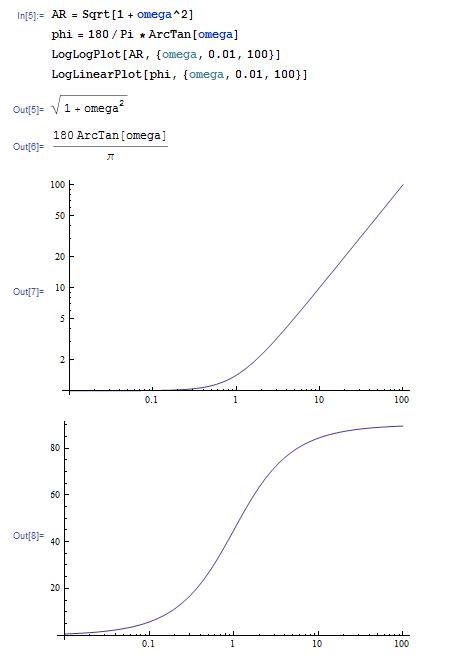
Presagie la gráfica para el controlador PID, usando la función\ Manipulate” para observar el efecto de variar los valores de Tau_I y Tau_D:
Manipular [LogLogPlot [Sqrt [1 + (Omega*taud - 1/ (Taui*Omega)) ^2], {omega,0.01,100}], {taui,0.1,10}, {taud,0,10}]
Manipular [LoglinearPlot [180/pi*Arctan [Omega*taud - 1/ (taui*omega)], {omega,0.01,100}], {taui,0.1,10}, {taud,0,10}]
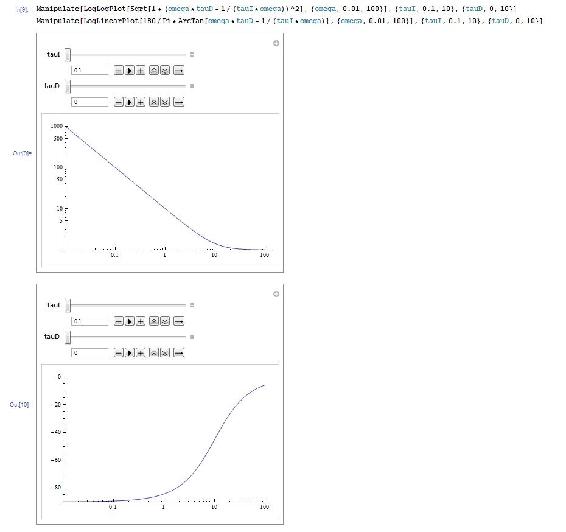
Gráfica de presagiación para el funcionamiento en bucle abierto de un sistema de tercer orden con un controlador P:
AR = Sqrt [1/ (1+omega^2)] *Sqrt [1/ (1+omega^2)] *Sqrt [1/ (1+25*omega ^ 2)] phi = 180/pi* (ArcTan [-omega] + ArcTan [-omega] + ArcTan [-5*omega]) LogLogPlot [AR, {omega,0.01,100}] LogLinearPlot [phi, omega,0.01,100}]
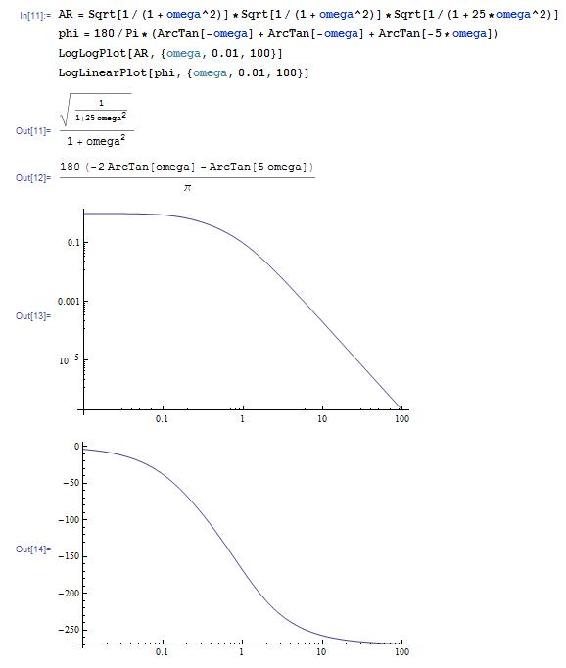
Encuentra frecuencia de cruce:
FindRoot [phi==-180, {omega,1}]
Esto produce omega = 1.18322 que es la frecuencia de cruce, y se puede utilizar para determinar la relación de amplitud (pedir matemática para AR) la ganancia (kC=1/Ar)
Para determinar en qué se debe establecer la ganancia en un margen de fase de 30 grados (condiciones de operación seguras) use lo siguiente en matemática:
FindRoot [phi==-150, {omega,1}]
El margen de fase de Cohen-Coon y otros análisis de frecuencia (como Zielger-Nicholas) se puede calcular utilizando el valor de ganancia (Kc) obtenido del método a escribir lo siguiente en mathatica:
nSolve [KC*ar==1, omega]
Derivaciones
Asumir un proceso de primer orden con entrada\(X(t)\)\(Y(t)\), salida y operador
\[\hat{G}^{-1}=\left(\tau \frac{\delta}{\delta t}+1\right)\nonumber \]
donde
\[X(t)=\hat{G}^{-1} Y(t)=\left(\tau \frac{\delta}{\delta t}+1\right) Y(t)=\tau Y^{\prime}(t)+Y(t) \label{1} \]
Para Bode Plot Analysis, asumimos una entrada periódica al sistema:
\[X(t) = \sin(ωt)\nonumber \]
Con base en esta entrada, podemos plantear la hipótesis de que:
\[Y(t) = AR * \sin(ωt + φ)\nonumber \]
A partir de esta hipótesis, podemos reemplazar la Ecuación\ ref {1} con nuestras funciones para\(X(t)\) y\(Y(t)\). Esto se muestra a continuación.
\[X(t) = \tau Y'(t) + Y(t) \label{1a} \]
\[\begin{align} \sin (\omega t) &=\tau \frac{\delta}{\delta t}(A R \sin (\omega t+\phi))+A R \sin (\omega t+\phi) \label{2} \\[4pt] &= AR(τω \cos(ωt + φ)) + \sin(ωt + φ) \label{3} \end{align} \]
Usando identidades trigonométricas, podemos reemplazar\(\cos(ωt + φ)\) con\(\cos(ωt)cos(φ) − \sin(ωt)sin(φ)\) y\(\sin(ωt + φ)\) con\(\sin(ωt)cos(φ) + \cos(ωt)sin(φ)\) para obtener:
\[\sin (\omega t)=A R(\omega T(\cos (\omega t) \cos (\varphi)-\sin (\omega t) \sin (\varphi))+\sin (\omega t) \cos (\varphi)+\cos (\omega t) \sin (\varphi)) \label{4a} \]
Para resolver para\(AR\) y\(φ\), podemos hacer coincidir los coeficientes para el\(\sin(ωt)\) término y\(\cos(ωt)\) término en el lado izquierdo y derecho de la Ecuación\ ref {4a}.
Coeficiente de\(\cos(ωt)\):
\[0 = AR(ωτ\cos(φ) + \sin(φ)) \label{5} \]
Coeficiente de\(\sin(ωt)\):
\[1 = AR( − ωτ\sin(φ) + \cos(φ)) \label{6} \]
De la Ecuación\ ref {5}, podemos dividir ambos lados por\(AR\cos(φ)\) y reordenarlos para obtener:
\[\tan (\phi)=-\omega \tau \label{7a} \]
o
\[\phi=\tan^{-1}(-\omega \tau) \label{7b} \]
A partir de esta relación, podemos dibujar un triángulo con el ángulo\(φ\) y la relación que se muestran en la Ecuación\ ref {7b}. A continuación se muestra una imagen del triángulo.
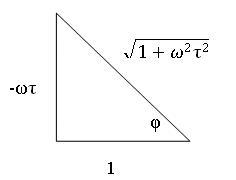
A partir de la Ecuación\ ref {6} y el triángulo anterior, podemos resolver para AR:
\[\begin{align} AR &=\frac{1}{-\omega \tau(\sin (\phi))+\cos (\phi)} \\[4pt] &=\frac{1}{-\omega \tau\left(\frac{-\omega \tau}{\sqrt{1+\omega^{2} \tau^{2}}}\right)+\frac{1}{\sqrt{1+\omega^{2} \tau^{2}}}} \\[4pt] &=\frac{1}{\sqrt{1+\omega^{2} \tau^{2}}} \label{8} \end{align} \]
Determinación de ganancia estable del controlador y margen de fase
El ajuste a través del margen de fase es un método más preciso que el ajuste a través de la Regla Cohen-Coon y la Regla de Afinación Ziegler-Nichols Podemos encontrar la ganancia y el margen de fase mediante el uso de gráficos de bode o mediante un método analítico.
Para encontrar una ganancia segura del controlador, siga los siguientes pasos:
- Construir diagrama de Bode de\(\log AR\) versus\(\log ωτ\) y\(φ\) versus\(\log ωτ\)
- Utilice la parcela anterior para encontrar\(ωτ\) tal que\(φ = -180^o + φ_{PM}\).
- Uso\(ωτ\) encontrado del paso anterior para encontrar\(AR\) en\(\log AR\) versus\(\log ωτ\) parcela.
- \(K_{C s a f e}=\frac{1}{A R}\)
Para encontrar el margen de fase, siga los siguientes pasos:
- Construir gráfico de Bode de LogAR versus Log ωτ y φ versus Log ωτ
- Utilice la gráfica anterior para encontrar ωτ tal que AR=1.
- Utilice ωτ que se encuentra del paso anterior para encontrar φ en φ versus Log ωτ.
- φ PM = 180 − | φ AR = 1 |
Encontrar la ganancia con un margen de fase:
- Usa tu expresión para Φ, establece Φ en el valor deseado y encuentra la raíz para ω.
- Ingrese el valor obtenido para ω en su expresión para AR.
- \(K_{C}=\frac{1}{A R}\)
Encontrar el margen de fase con una ganancia:
- Usa tu expresión para AR, establecer
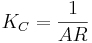y resolver para ω. - Ingrese el valor obtenido para ω en su expresión para Φ.
Determinar la pendiente de una gráfica de Bode
En ocasiones es necesario determinar la forma relativa de una Gráfica de Bode sin el uso de una computadora o solucionador de ecuaciones ODE. Al esbozar la forma relativa, hay tres partes principales de una Gráfica de Bode básica que deben ser consideradas.
- Punto de cruce
- Valor inicial
- Pendiente
Punto de Cruce
El punto de cruce de la Gráfica de Bode es cuando la frecuencia, ω, es igual a 1/τ. Si el eje x de la Gráfica de Bode es ωτ, el punto de cruce estará en el eje x = 1. Si hay múltiples valores de τ, puede haber múltiples puntos de cruce, cada uno en la frecuencia donde ω es igual a 1/τ. Si hay múltiples valores τ, y el eje x es ωτ, se debe especificar a qué τ se refiere el eje x.
Valor inicial
El valor inicial depende de los\(K_P\) valores\(K_C\) y que contribuyen al proceso.
Pendiente
La pendiente para un proceso incontrolado es igual a la negativa del orden del proceso. Por ejemplo, si hay un proceso de primer orden sin controlador la pendiente de la Parcela de Bode sería -1 (-1 para primer orden), después de que se haya alcanzado el punto de cruce. A continuación se muestra una imagen de esta trama de Bode.
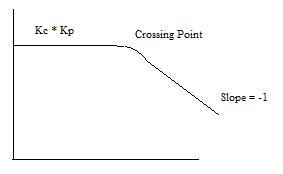
Para un proceso controlado por un controlador PD, el AR es esencialmente el inverso del sistema de primer orden AR, lo que significa que la suma de pendiente de un controlador PD es un +1, en lugar de un -1 como en un proceso de primer orden. Para un sistema de segundo orden con controlador PD la pendiente final será -1 (-2 del proceso de segundo orden, +1 de PD). Sin embargo, puede haber múltiples puntos de cruce, cuya ubicación depende del valor de τ P y τ D. Recuerda que el punto de cruce es donde ωτ es igual a uno. Dado que la contribución de pendiente solo viene después del punto de cruce, una Parcela de Bode para τ D menor que τ P se vería como la imagen de abajo.
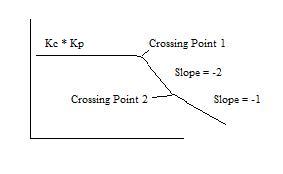
- El punto de cruce 1 es donde ωτ P es 1 y el punto de cruce 2 es donde ωτ D es 1.
- De igual manera, si τ D es mayor que τ, la pendiente pasaría primero a +1, luego a -1.
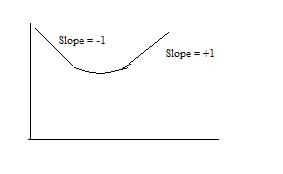
Para un controlador PI, la contribución de pendiente del controlador viene antes del punto de cruce, y luego pasa a cero después del punto de cruce. Por lo tanto, un controlador PID se vería como la imagen que se muestra a continuación, asumiendo τ D = τ I.
Usted es ingeniero de controles y desea caracterizar un intercambiador de calor utilizado en un proceso químico. Una de las muchas cosas que le interesa saber sobre el sistema es cómo la temperatura de salida caliente responde a las fluctuaciones en el caudal de entrada. Usando datos para un caudal de entrada en particular, usted graficó normalizado (¿por qué?) caudal y temperatura normalizada de salida caliente vs. frecuencia (rad/min). Utilice esta gráfica para determinar la relación de amplitud.
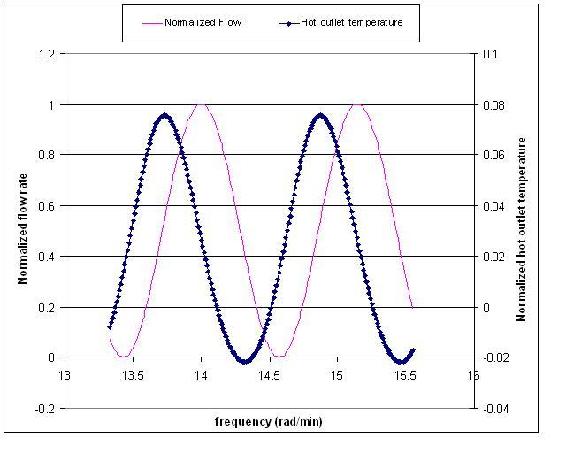
Solución
Debido a que las unidades de caudal y temperatura no tienen las mismas unidades, estos valores necesitaban normalizarse antes de calcular la relación de amplitud. Para normalizar el flujo, utilice la siguiente ecuación:
\[\text {F}_\text{norm}=\frac{F-\text {Fmin}}{\text {Fmax}-\text {Fmin}} \nonumber \nonumber \]
donde\(F\) es el caudal de un punto de datos en particular.
En este problema la temperatura\(T\),, está en ˚C, entonces
\[\text {Tnorm}=\frac{T-273.15}{100} \nonumber \nonumber \]
Para encontrar la amplitud de ambas funciones de onda, primero recuerde que la amplitud de una ola es la altura máxima de una cresta de onda (o profundidad de un canal). Para una onda de estado estacionario producida a partir de una columna de valores en Excel, puede calcular rápidamente la amplitud usando las funciones de Excel max () y min (). [Esto se puede encontrar usando la ayuda de Excel.] Si optó por encontrar la amplitud de esta manera, entonces la amplitud para una función de onda única sería
\[\text {Amplitude}=\frac{[\max ()-\min ()]}{2} \nonumber \nonumber \]
Tenga en cuenta que esta es solo una forma de encontrar la amplitud de una onda. También se podría encontrar simplemente leyendo los valores de la gráfica de una onda.
Una vez que se encuentren las amplitudes de las ondas de entrada y salida, utilice los valores para encontrar la relación de amplitud, AR, de la siguiente manera:
\[AR=\frac{\text { outlet streams amplitude }}{\text {inlet streams amplitude}}=\frac{0.0486}{0.499}=0.0974\nonumber \]
El siguiente gráfico muestra cómo el flujo de entrada y las temperaturas de salida tanto caliente como fría varían como funciones sinusoidales del tiempo. Esta gráfica se generó utilizando los mismos datos para el intercambiador de calor del Ejemplo 1. Utilice esta gráfica para encontrar el desplazamiento de fase entre el flujo de entrada y la corriente de salida caliente.
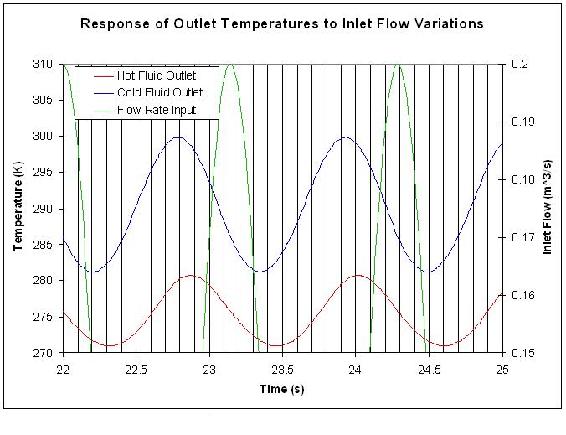
Solución
Determinar el periodo (P) — Esto se puede hacer encontrando el tiempo de un pico al siguiente de una onda dada. En este caso, queremos conocer el periodo del caudal de entrada, así\(P = 1.14\,s\).
Determinar el retraso (delta P) — Esto se puede hacer encontrando la diferencia de tiempo entre el pico del caudal de entrada y el pico de la corriente de salida caliente. (Recuerde que la ola de salida caliente va a la ola del caudal de entrada).
\(\delta P = 0.87s\)
\[\text {Phaseshift}=\frac{0.87\, s}{1.14\, s} *-2 \pi=-4.80\nonumber \]
Dado que solo nos preocupan los valores de tiempo para encontrar el cambio de fase, los datos no necesitan normalizarse.
Referencias
- Bechette, B. Wayne. Control de Procesos: Modelado, Diseño y Simulación. pp 172-178, 214-235. Upper Saddle River, N.J. Prentice Hall, PTR 2003.
- Liptak, Bela G. Control y Optimización de Procesos. Volumen 2. Manual de Ingenieros de Instrumentos. Cuarta Edición. CRC Press, Boca Ratón Fl. 2003. Insertformulaaquí
Colaboradores y Atribuciones
- escrito por: Tony Martus, Kegan Lovelace, Daniel Patrick, Merrick Miranda, Jennifer DeHeck, Chris Bauman, Evan Leonard
- Editado por: Alfred Chung (Derivaciones), Ran Li (Determining Stable Controller Gain), Nirala Singh (Determining Slope of Bode Plot), Katy Kneiser e Ian Sebastian (síntesis con 2006 wiki “Bode Plot”), Robert Appel, Jessica Rilly y Jordan Talia (Formateo