10.3: Valores propios y vectores propios

Última actualización
Guardar como PDF

Page ID: 85562

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

¿Qué son los vectores propios y los valores propios?

Los vectores propios (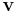 mathbf ) y los valores propios ($λ$) son herramientas matemáticas utilizadas en una amplia gama de aplicaciones. Se utilizan para resolver ecuaciones diferenciales, problemas armónicos, modelos de población, etc. en Ingeniería Química se utilizan principalmente para resolver ecuaciones diferenciales y para analizar la estabilidad de un sistema.

Definición: Eigenvector y Eigenvalues

Un vector propio es un vector que mantiene su dirección después de sufrir una transformación lineal.
Un Eigenvalue es el valor escalar por el que se multiplicó el vector propio durante la transformación lineal.

Los vectores propios y los valores propios se explican mejor usando un ejemplo. Echa un vistazo a la imagen de abajo.

ona Lisa con eigenvector.jpg

En la imagen de la izquierda, se dibujaron dos vectores en la Mona Lisa. El cuadro entonces bajo fue una transformación lineal y se muestra a la derecha. El vector rojo mantuvo su dirección; por lo tanto, es un vector propio para esa transformación lineal. El vector azul no mantuvo a su director durante la transformación; por lo tanto, no es un vector propio. El valor propio para el vector rojo en este ejemplo es 1 porque la flecha no se alargó ni acortó durante la transformación. Si el vector rojo, a la derecha, tuviera el doble de tamaño que el vector original entonces el valor propio sería 2. Si el vector rojo estuviera apuntando directamente hacia abajo y permaneciera del tamaño en la imagen, el valor propio sería -1.

Ahora que tienes una idea de lo que son un vector propio y un valor propio podemos empezar a hablar de las matemáticas detrás de ellos.

Ecuación Fundamental

La siguiente ecuación debe ser verdadera para los vectores propios y los valores propios dados una matriz cuadrada$\mathrm{A}$:

\[\mathrm{A} \cdot \mathrm{v}=\lambda \cdot \mathrm{v} \label{eq1} \]

donde:

$\mathrm{A}$es una matriz cuadrada
$\mathrm{v}$es el Eigenvector
$\lambda$es el valor propio

Pasemos por un ejemplo sencillo para que entiendas mejor la ecuación fundamental.

Ejemplo$\PageIndex{1}$

¿Es$\mathbf{v}$ un vector propio con el correspondiente$λ = 0$ para la matriz$\mathbf{A}$?

\[\mathbf{v}=\left[\begin{array}{c} 1 \\ -2 \end{array}\right] \nonumber \nonumber \]

\[\mathbf{A}=\left[\begin{array}{cc} 6 & 3 \\ -2 & -1 \end{array}\right] \nonumber \nonumber \]

Solución

\[\begin{align*} A \cdot \mathbf{v} &= \lambda \cdot \mathbf{v} \\[4pt] \left[\begin{array}{cc} 6 & 3 \\ -2 & -1 \end{array}\right] \cdot\left[\begin{array}{c} 1 \\ -2 \end{array}\right] &=0\left[\begin{array}{c} 1 \\ -2 \end{array}\right] \\[4pt] \left[\begin{array}{l} 0 \\ 0 \end{array}\right] &=\left[\begin{array}{l} 0 \\ 0 \end{array}\right] \end{align*}\nonumber \]

Por lo tanto, es cierto que$\mathbf{v}$ y$λ = 0$ son un vector propio y un valor propio respectivamente, para$\mathbf{A}$. (Ver sección sobre Operaciones matriciales, es decir, multiplicación matricial)

Cálculo de valores propios y vectores propios

El cálculo de los valores propios y los vectores propios correspondientes se completa utilizando varios principios de álgebra lineal. Esto se puede hacer a mano, o para situaciones más complejas se puede usar una multitud de paquetes de software (es decir, Mathematica). La siguiente discusión funcionará para cualquier matriz n x n; sin embargo, en aras de la simplicidad, se utilizan matrices más pequeñas y manejables. Tenga en cuenta también que a lo largo de este artículo, el tipo negrita se utiliza para distinguir matrices de otras variables.

Revisión de álgebra lineal

Para aquellos que no están familiarizados con el álgebra lineal, esta sección está diseñada para dar los conocimientos necesarios utilizados para calcular los valores propios y vectores propios. Para una discusión más extensa sobre álgebra lineal, consulte las referencias.

Operaciones de Matriz Básicas

Una matriz m x n A es una matriz rectangular de$mn$ números (o elementos) dispuestos en filas horizontales (m) y columnas verticales (n):

\ [\ boldsymbol {A} =\ left [\ begin {array} {lll}
a_ {11} & a_ {1 j} & a_ {1 n}\\
a_ {i 1} & a_ {i j} & a_ {i n}\\
a_ {m 1} & a_ {m j} & a_ {m n}
\ end {array}\ derecha]\ nonumber\]

Para representar una matriz con el elemento aij en la i-ésima fila y j ésima columna, usamos la abreviatura A = [aij]. Se dice que dos m x n matrices A = [aij] y B = [bij] son iguales si los elementos correspondientes son iguales.

Suma y resta

Podemos agregar A y B agregando los elementos correspondientes:

\[A + B = [a_{ij}] + [b_{ij}] = [a_{ij} + b_{ij}\nonumber \]

Esto le dará al elemento en la fila i y columna j de C = A + B tener

\[c_{ij} = a_{ij} + b_{ij}.\nonumber \]

Se puede encontrar una suma y resta más detallada de matrices en el siguiente ejemplo.

\ [\ left [\ begin {array} {ccc}
1 & 2 & 6\\
4 & 5 & 10\\
5 & 3 & 11
\ end {array}\ right] +\ left [\ begin {array} {ccc}
8 & 3 & 5\\
5 & 4 & 4\\
3 & 0 & 6
\ end {array}\ right] =\ left [\ begin {array} {ccc}
1+8 & 2+3 & 6+5\\
4+5 & 5+4 & 10+4\\
5+3 & 3+0 & 11+6
\ end {array}\ right] =\ left [\ begin {array} {ccc}
9 & 5 & 11\\
9 & 9 & 14\\
8 & 3 & 17
\ end {array}\ derecha]\ nonumber\]

Multiplicación

La multiplicación de matrices NO se realiza de la misma manera que la suma y resta. Veamos la siguiente multiplicación matricial:

\[A \times B=C\nonumber \]

$A$es una$m \times n$ matriz,$B$ es una$n \times p$ matriz, y$C$ es una$m \times p$ matriz. Por lo tanto, la matriz resultante$C$, tiene el mismo número de filas que la primera matriz y el mismo número de columnas que la segunda matriz. También el número de columnas en la primera es el mismo que el número de filas en la segunda matriz.

El valor de un elemento en C (fila i, columna j) está determinado por la fórmula general:

\[c_{i, j}=\sum_{k=1}^{n} a_{i, k} b_{k, j}\nonumber \]

Por lo tanto,

\ [\ begin {align*}\ left [\ begin {array} {ccc}
1 & 2 & 6\\
4 & 5 & 10\\
5 & 3 & 11
\ end {array}\ right]\ left [\ begin {array} {cc}
3 & 0\\
0 & 1\\
5 & 1
\ end {array}\ derecha] &=\ left [\ begin {array} {cc}
1\ times 3+2\ times 0+6\ times 5 & 1\ times 0+2\ times 1+6\ times 1\\
4\ times 3+5\ times 0+10\ times 5 & 4\ times 0+5\ times 1+10\ times 1\\ times 1\\
5\ times 3+3\ times 0+11\ times 5 & 5\ times 0+3\ times 1+11\ veces 1
\ end {array}\ derecha]\\ [4pt] &=\ left [\ begin {array} {cc}
33 & 8\\
62 & 15\\
70 & 14
\ end {array}\ derecha]\ end {align*}\ nonumber\]

También se puede observar que la multiplicación de matrices no es conmutativa (A B ≠ B A). La multiplicación de una matriz por un escalar se realiza multiplicando cada elemento por el escalar.
c A = A c = [caij]

\ [2\ left [\ begin {array} {ccc}
1 & 2 & 6\\
4 & 5 & 10\\
5 & 3 & 11
\ end {array}\ right] =\ left [\ begin {array} {ccc}
2 & 4 & 12\\
8 & 10 & 20\\
10 & 6 & 22
\ end {array}\ derecha]\ nonumber\]

Matriz de Identidad

La matriz de identidad es una matriz especial cuyos elementos son todos ceros excepto a lo largo de la diagonal primaria, que están ocupados por unos. La matriz de identidad puede ser de cualquier tamaño siempre que el número de filas sea igual al número de columnas.

\ [\ mathbf {I} =\ left [\ begin {array} {llll}
1 & 0 & 0 & 0\\
0 & 1 & 0 & 0 & 0\\
0 & 0 & 0 & 1 &
0 & 0 & 0 & 0 & 1
\ end {array}\ derecha]\ nonumber\]

Determinante

El determinante es una propiedad de cualquier matriz cuadrada que describa el grado de acoplamiento entre ecuaciones. Para una matriz de 2x2 el determinante es:

\ [\ nombreoperador {det} (\ mathbf {A}) =\ izquierda|\ begin {array} {ll}
a & b\\
c & d
\ end {array}\ derecha|=a d-b c\ nonumber\]

Tenga en cuenta que las líneas verticales alrededor de los elementos de la matriz denota el determinante. Para una matriz de 3x3 el determinante es:

\ [\ nombreoperador {det} (\ mathbf {A}) =\ izquierda|\ begin {array} {lll}
a & b & c\\
d & e & f\\
g & h & i
\ end {array}\ derecha|=a\ izquierda|\ begin {array} {cc}
e & f\\
h & i
\ end {array}\ derecha|-b\ izquierda|\ begin {array} {cc}
d & f\\
g & i
\ end {array}\ derecha|+c\ izquierda|\ begin {array} {cc}
d & e\
g & h
\ end {array}\ derecha|=a (e i-f h) -b (d i-f g) +c (d h-e g)\ nonumber\]

Las matrices más grandes se calculan de la misma manera donde el elemento de la fila superior se multiplica por el determinante de la matriz restante una vez que se eliminan la fila y la columna de ese elemento. Términos donde se agregan los elementos superiores en columnas impares y términos donde se restan los elementos superiores en filas pares (asumiendo que el elemento superior es positivo). Sin embargo, para matrices mayores de 3x3; probablemente sea más rápido usar software matemático para hacer estos cálculos, ya que rápidamente se vuelven más complejos al aumentar el tamaño.

Resolviendo valores propios y vectores propios

Los autovalores (λ) y los vectores propios (v), están relacionados con la matriz cuadrada A mediante la siguiente ecuación. (Nota: Para que se computen los valores propios, la matriz debe tener el mismo número de filas que las columnas).

\[(\mathbf{A}-\lambda \mathbf{I}) \cdot \mathbf{v}=0\nonumber \]

Esta ecuación es solo un reordenamiento de la Ecuación\ ref {eq1}. Para resolver esta ecuación, los valores propios se calculan primero estableciendo det (A-λ I) a cero y luego resolviendo para λ. El determinante se establece en cero con el fin de asegurar soluciones no triviales para v, por un teorema fundamental de álgebra lineal.

\ [A=\ left [\ begin {array} {lll}
4 & 1 & 4\\
1 & 7 & 1\\
4 & 1 & 4
\ end {array}\ derecha]\ nonumber\]

\ [A-\ lambda I=\ left [\ begin {array} {lll}
4 & 1 & 4\\
1 & 7 & 1\\
4 & 1 & 4 & 4
\ end {array}\ derecha] +\ left [\ begin {array} {ccc}
-\ lambda & 0 & 0\\
0 & -\ lambda & 0\\ lambda &
0\\ 0 & -\ lambda
\ end {array}\ derecha]\ nonumber\]

\ [\ nombreoperador {det} (A-\ lambda I) =\ izquierda|\ begin {array} {ccc}
4-\ lambda & 1 & 4\\
1 & 7-\ lambda & 1\\
4 & 1 & 4-\ lambda
\ end {array}\ derecha|=0\ nonumber\]

\ [\ begin {array} {l}
-54\ lambda+15\ lambda^ {2} -\ lambda^ {3} =0\\
-\ lambda (\ lambda-6) (\ lambda-9) =0\\
\ lambda=0,6,9
\ end {array}\ nonumber\]

Para cada uno de estos autovalores, se calcula un vector propio que satisfará la ecuación (A-λ I) v =0 para ese valor propio. Para ello, un valor propio se sustituye en A-λ I, y luego se utiliza el sistema de ecuaciones para calcular el vector propio. Para$λ = 6$

\ [(\ mathbf {A} -6\ mathbf {I})\ mathbf {v} =\ left [\ begin {array} {ccc}
4-6 & 1 & 4\\
1 & 7-6 & 1\\
4 & 1 & 4-6
\ end {array}\ right]\ left [\ begin {array} {l}
x\\
y\
z
\ end {array} \ derecha] =\ izquierda [\ begin {array} {ccc}
-2 & 1 & 4\\
1 & 1 & 1 & 1\\
4 & 1 & -2
\ end {array}\ right]\ left [\ begin {array} {l}
x\\
y\
z
\ end {array}\ right] =0\ nonumber\]

Usando la multiplicación obtenemos un sistema de ecuaciones que se pueden resolver.
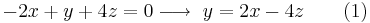
$2x+y+4z = 0\ largofila derecha\ y = 2x-4z\ qquad (1)$
$+y+z = 0\ largofila derecha\ y = -x-z\ qquad (2)$
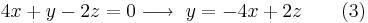
$x+y-2z = 0\ largofila derecha\ y = -4x+2z\ qquad (3)$
Equiparar (1) y (3)...
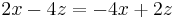
$x-4z=-4x+2z\ qquad$
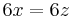
$x=6z\ qquad$
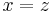
$=z\ qquad$
Conectando esto en (2)...
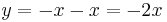
$=-x-x=-2x\ qquad$
Hay un grado de libertad en el sistema de ecuaciones, así que tenemos que elegir un valor para una variable. Por convención elegimos x = 1 entonces
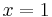
$=1\ qquad$
$=-2\ qquad$
$=1\ qquad$
$mathbf {v} =\ begin {bmatrix} 1\\ -2\\ 1\ end {bmatrix}$
Un grado de libertad siempre ocurre porque en estos sistemas no todas las ecuaciones resultan ser independientes, es decir, dos ecuaciones diferentes pueden ser simplificado a la misma ecuación. En este caso se eligió un número pequeño (x = 1) para mantener la solución simple. Sin embargo, está bien elegir cualquier número para x, lo que significa que cada valor propio tiene potencialmente un número infinito de posibles vectores propios que se escalan en función del valor inicial de x elegido. Dicho de otra manera, el autovector sólo apunta en una dirección, pero la magnitud de este puntero no importa. 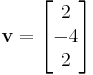Para este ejemplo, obtener un autovector que $mathbf {v} =\ begin {bmatrix} 1\\ -2\\ 1\ end {bmatrix}$ es idéntico a obtener un autovector que es $mathbf {v} =\ begin {bmatrix} 2\\ -4\\ 2\ end {bmatrix}$ o un autovector que es escalado por alguna constante, en este caso 2.

Terminando las calcuciones, se repite el mismo método para λ = 0 y λ = 9 para obtener sus vectores propios correspondientes.
Para λ = 0,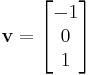 $mathbf {v} =\ begin {bmatrix} -1\\ 0\\ 1\ end {bmatrix}$
Para λ = 9,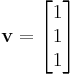 $mathbf {v} =\ begin {bmatrix} 1\\ 1\\ 1\ end {bmatrix}$

Para verificar sus respuestas, puede volver a enchufar sus valores propios y vectores propios en la ecuación gobernante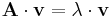 $mathbf {A}\ cdot\ mathbf {v} =\ lambda\ cdot\ mathbf {v}$ . Para este ejemplo, λ = 6 y $mathbf {v} =\ begin {bmatrix} 1\\ -2\\ 1\ end {bmatrix}$ se comprobó dos veces.

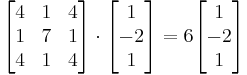
$begin {bmatrix} 4&1&4\\ 1&7&1\\ 4&1&4\ end {bmatrix}\ cdot\ begin {bmatrix} 1\\ -2\ 1\ end {bmatrix} =6\ begin {bmatrix} 1\\ -2\ 1\ end {bmatrix}$

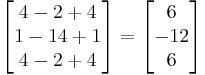
$begin {bmatrix} 4-2+4\\ 1-14+1\\ 4-2+4\ end {bmatrix} =\ begin {bmatrix} 6\\ -12\\ 6\ end {bmatrix}$

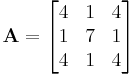Por lo tanto, λ = 6 y $mathbf {v} =\ begin {bmatrix} 1\\ -2\\ 1\ end {bmatrix}$ son ambos un par autovalor-vector propio para la matriz $mathbf {A} =\ begin {bmatrix} 4&1&4\\ 1&7&1\\ 4&1&4\ end {bmatrix}$ .

Cálculo de valores propios y vectores propios mediante software numérico

Valores propios en Mathematica

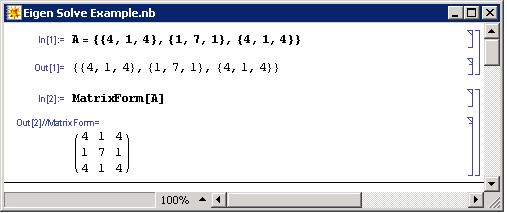
Para matrices más grandes (4x4 y mayores), resolver los valores propios y vectores propios se vuelve muy largo. Por lo tanto, se utilizan programas de software como Mathematica. El ejemplo de la última sección se utilizará para demostrar cómo usar Mathematica. Primero podemos generar la matriz A. Esto se hace usando la siguiente sintaxis:

$A = \{\{4,1,4\},\{1,7,1\},\{4,1,4\}\}$

Se puede observar que la matriz se trata como una lista de filas. Los elementos de la misma fila están contenidos en un solo conjunto de corchetes y separados por comas. El conjunto de filas también están contenidas en un conjunto de corchetes y están separadas por comas. Una captura de pantalla de esto se ve a continuación. (Nota: El comando “MatrixForm []” se utiliza para mostrar la matriz en su forma estándar. También en Mathematica debes presionar Shift + Enter para obtener una salida.)

A continuación encontramos el determinante de la matriz A-λ I, restando primero la matriz λ I de A (Nota: Esta nueva matriz, A -λ I, se ha denominado A2).

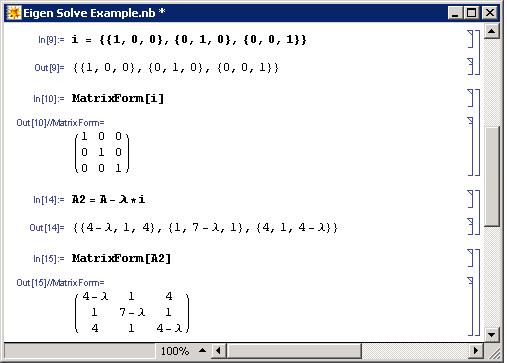
El comando para encontrar el determinante de una matriz A es:

Det [A]

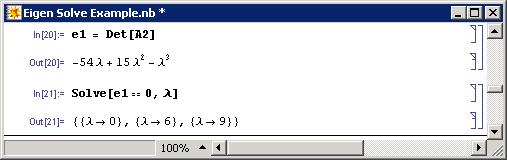
Para nuestro ejemplo el resultado se ve a continuación. Al establecer esta ecuación en 0 y resolver para λ, se encuentran los valores propios. Para ello se utiliza la función Solve []. Observe en la sintaxis que el uso de dos signos iguales (==) se usa para mostrar equivalencia mientras que un solo signo igual se usa para definir una variable.

Resolver [{conjunto de ecuaciones}, {variables que se están resolviendo}]

Alternativamente, los valores propios de una matriz A se pueden resolver con la función Autovalor de Mathematica []:

Valores propios [A]

Obsérvese que se obtienen los mismos resultados para ambos métodos.

Para encontrar los vectores propios de una matriz A, la función Eigenvector [] se puede utilizar con la sintaxis siguiente.

Autovectores [A]

Los vectores propios se dan en orden de valores propios descendentes.

Una función más que es útil para encontrar valores propios y vectores propios es Eigensystem []. Esta función se llama con la siguiente sintaxis.

Sistema propio [A]

En esta función, el primer conjunto de números son los valores propios, seguidos de los conjuntos de vectores propios en el mismo orden que sus valores propios correspondientes.

El archivo de Mathematica utilizado para resolver el ejemplo se puede encontrar en este enlace.MEDIA:EIGEN Resolver ejemplo.NB

Microsoft Excel

Microsoft Excel es capaz de resolver valores propios de matrices simétricas utilizando su función Goal Seek. Una matriz simétrica es una matriz cuadrada que es igual a su transposición y siempre tiene números reales, no complejos, para los valores propios. En muchos casos, no se pueden encontrar valores propios complejos usando Excel. La búsqueda de objetivos se puede utilizar porque encontrar el valor propio de una matriz simétrica es análogo a encontrar la raíz de una ecuación polinómica. El siguiente procedimiento describe cómo calcular el valor propio de una matriz simétrica en el tutorial de Mathematica usando MS Excel.

(1) Ingrese los valores que se muestran a continuación para la matriz A luego haga clic en el menú INSERT-NOMBRE-DEFINIR “Matrix_A” para nombrar la matriz.

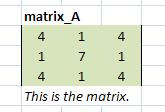
IgenExcel (1) .MX

(2) De igual manera, defina la matriz de identidad I ingresando los valores que se muestran a continuación y luego nombrándola “Matrix_I”.

IgenExcel (2) .jpg

(3) Ingresa una suposición inicial para el valor propio y luego nombra “lambda”.

IgenExcel (3) ..MX

(4) En una celda vacía, escriba la fórmula =Matrix_a-lambda*matrix_i Resalte tres celdas a la derecha y hacia abajo, presione F2, luego presione CRTL+MAYÚS+ENTRAR. Nombra esta matriz “Matrix_a_lambda_I”.

IgenExcel (4) .jpg

(5) En otra celda, ingrese la fórmula =MDETERM (Matrix_a_lambda_I). Esta es la fórmula determinante para Matrix_a_lambda_I.

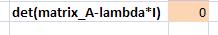
IgenExcel (5) .jpg

(6) Haga clic en el menú Herramientas-Objetivo Buscar... y establezca la celda que contiene la fórmula determinante a cero cambiando la celda que contiene lambda.

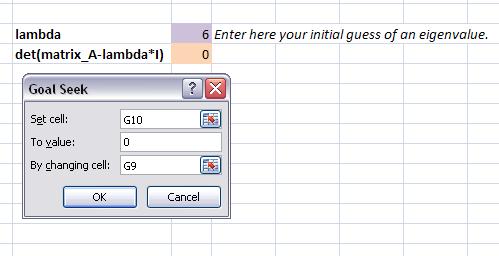
IgenExcel (6) .jpg

(7) Para obtener los tres valores propios para la matriz A, vuelva a ingresar diferentes conjeturas iniciales. Excel calcula el valor propio más cercano al valor de la suposición inicial. Se determinó que los valores propios para la matriz A fueron 0, 6 y 9. Por ejemplo, las conjeturas iniciales de 1, 5 y 13 conducirán a valores propios de 0, 6 y 9, respectivamente.

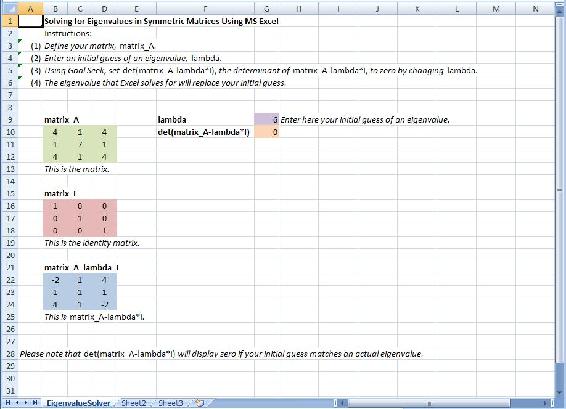
IgenExcel (8) .jpg

La hoja de cálculo de MS Excel utilizada para resolver este problema, vista arriba, se puede descargar desde este enlace: Media:ExcelSolveEigenValue.xls.

Aplicaciones de ingeniería química

El método de autovalor y autovector de análisis matemático es útil en muchos campos porque puede ser utilizado para resolver sistemas lineales homogéneos de ecuaciones diferenciales con coeficientes constantes. Además, en ingeniería química muchos modelos se forman sobre la base de sistemas de ecuaciones diferenciales que son lineales o pueden linealizarse y resolverse utilizando el método de autovalor propio. En general, la mayoría de las ODE pueden linealizarse y, por lo tanto, resolverse mediante este método. Linealización de ODEs Por ejemplo, un dispositivo de control PID se puede modelar con ODEs que pueden linealizarse donde se puede implementar entonces el método de autovector de valor propio. Si tenemos un sistema que se puede modelar con ecuaciones diferenciales lineales que involucran temperatura, presión y concentración a medida que cambian con el tiempo, entonces el sistema se puede resolver usando valores propios y vectores propios:

\[\frac{d P}{d t}=4 P-4 T+C\nonumber \]

\[\frac{d T}{d t}=4 P-T+3 C\nonumber \]

\[\frac{d C}{d t}=P+5 T-C\nonumber \]

Nota: Este no es un modelo real y simplemente sirve para introducir el método eigenvalue y eigenvector.

A es solo la matriz que representa los coeficientes en las ecuaciones diferenciales lineales anteriores. No obstante, al configurar la matriz, A, el orden de los coeficientes importa y debe permanecer consistente. Es decir, en la siguiente matriz representativa, la primera columna corresponde a los coeficientes de P, la segunda columna a los coeficientes de T, y la tercera columna corresponde a los coeficientes de C. Lo mismo ocurre con las filas. 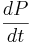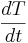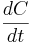La primera fila corresponde a $frac {dP} {dt}$ , la segunda fila corresponde a $frac {dT} {dt}$ , y la tercera fila corresponde a $frac {dC} {dt}$ :

\ [\ mathbf {A} =\ left [\ begin {array} {ccc}
4 & -4 & 1\\
4 & -1 & 3\\
1 & 5 & -1
\ end {array}\ derecha]\ nonumber\]

Es de destacar que la matriz A sólo se llena de constantes para un sistema lineal de ecuaciones diferenciales. Este resulta ser el caso porque cada componente de la matriz es el diferencial parcial de una variable (en este caso P, T o C). Es este diferencial parcial el que produce una constante para los sistemas lineales. Por lo tanto, la matriz A es realmente la matriz jacobiana para un sistema diferencial lineal.

Ahora, podemos reescribir el sistema de ODE arriba en forma de matriz.

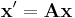
$mathbf {x'} =\ mathbf {hacha}$

donde

\ [\ mathbf {x} (t) =\ left [\ begin {array} {l}
P (t)\\
T (t)\\
C (t)
\ end {array}\ derecha]\ nonumber\]

Adivinamos soluciones de prueba de la forma

\[\mathbf{x}=\mathbf{v} e^{\lambda t}\nonumber \]

ya que cuando sustituimos esta solución en la ecuación matricial, obtenemos

\[\lambda \mathbf{v} e^{\lambda t}=\mathbf{A} \mathbf{v} e^{\lambda t}\nonumber \]

Después de cancelar el factor escalar distinto de cero e ^λt, obtenemos el problema de autovalor deseado.

\[\mathbf{A} \mathbf{v}=\lambda \mathbf{v}\nonumber \]

Así, hemos demostrado que

\[\mathbf{x}=\mathbf{v} e^{\lambda t}\nonumber \]

será una solución no trivial para la ecuación matricial siempre que v sea un vector distinto de cero y λ sea una constante asociada con v que satisfaga el problema del valor propio.

Para resolver los valores propios y vectores propios, reorganizamos la Ecuación\ ref {eq1} para obtener lo siguiente:

\ [\ left (\ begin {array} {lllll}
\ boldsymbol {\ lambda} &\ lambda\ mathbf {I})\ mathbf {v} =0 & & {\ left [\ begin {array} {ccc}
4-\ lambda & -4 & 1\\
4 & 1 &\ lambda & 3\\
1 & 5 & -1-\ lambda
\ end {array}\ derecha]\ cdot\ left [\ begin {array} {l}
x\\
y\\
z
\ end {array}\ right] =0}
\ end {array}\ right. \ nonumber\]

Para soluciones no triviales para v, el determinante de la matriz de valores propios debe ser igual a cero,$\operatorname{det}(\mathbf{A}-\lambda \mathbf{I})=0$. Esto nos permite resolver para los valores propios, λ. Se debe obtener, después de la simplificación, un polinomio de tercer orden, y por lo tanto tres valores propios. (ver sección sobre Resolver valores propios y vectores propios para más detalles) Usando los valores eigncalculados, se puede determinar la estabilidad del sistema cuando se altera (ver siguiente sección).

Una vez que haya calculado los tres valores propios, estará listo para encontrar los vectores propios correspondientes. Vuelva a enchufar los valores propios en la ecuación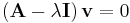 $izquierda (\ mathbf {A} -\ lambda\ mathbf {I}\ derecha)\ mathbf {v} =0$ y resuelva los vectores propios correspondientes. Debería haber tres vectores propios, ya que había tres autovalores. (ver sección sobre Cálculo de valores propios y vectores propios para más detalles)

La solución se verá así:

\ [\ left [\ begin {array} {l}
P (t)\\
T (t)\\
C (t)
\ end {array}\ right] =c_ {1}\ left [\ begin {array} {l}
x_ {1}\
y_ {1}\
z_ {1}
\ end {array}\ right] e^ {\ lambda_ {1} t} +c_ {2}\ left [\ begin {array} {l}
x_ {2}\\
y_ {2}\
z_ {2}
\ end {array}\ derecha] e^ {\ lambda_ {2} t} +c_ {3}\ left [\ begin {array} {l}
x_ {3}\
y_ {3}\\
z_ {3}
\ end {array}\ derecha] e^ {\ lambda_ {3} t}\ nonumber\]

donde
x ₁, x ₂, x ₃, y ₁, y ₂, y ₃, z ₁, z ₂, z ₃ son todas constantes de los tres vectores propios. La solución general es una combinación lineal de estos tres vectores de solución porque el sistema original de las ODE es homogéneo y lineal. Es homogéneo porque las expresiones derivadas no tienen términos cruzados, como PC o TC, y no dependen de t. Es lineal porque el operador derivado es lineal. Para resolver para c ₁, c ₂, c ₃ debe haber algunas condiciones iniciales dadas (ver Ejemplo 1 Trabajado).

Este Wiki no trata de resolver ODEs. Sólo se ocupa de resolver para los valores propios y vectores propios. En Mathematica la función Dsolve [] se puede utilizar para eludir los cálculos de valores propios y vectores propios para dar las soluciones para los diferenciales directamente. Consulte Usar valores propios y vectores propios para encontrar estabilidad y resolver ODEs para resolver ODEs usando el método de autovalores y vectores propios, así como con Mathematica.

Esta sección sólo pretendía introducir el tema de los valores propios y vectores propios y no trata de los detalles matemáticos que se presentan más adelante en el artículo.

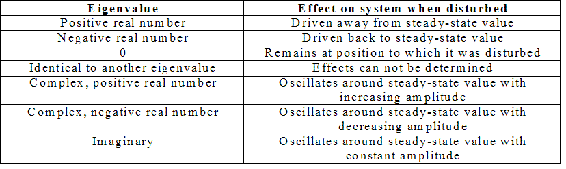
Uso de valores propios para determinar los efectos de perturbar un sistema

Los valores propios pueden ayudar a determinar tendencias y soluciones con un sistema de ecuaciones diferenciales. Una vez que se determinan los valores propios de un sistema, los valores propios pueden usarse para describir la capacidad del sistema para regresar al estado estacionario si se altera.

La forma más sencilla de predecir el comportamiento de un sistema en caso de perturbación es examinar los signos de sus valores propios. Los valores propios negativos harán que el sistema vuelva a su valor de estado estacionario, mientras que los valores propios positivos lo alejarán. ¿Qué sucede si hay dos valores propios presentes con signos opuestos? ¿Cómo responderá el sistema ante una perturbación en ese caso? En muchas situaciones, habrá un valor propio que tiene un valor absoluto mucho mayor que los otros autovalores correspondientes para ese sistema de ecuaciones diferenciales. Esto se conoce como el “valor propio dominante”, y tendrá el mayor efecto en el sistema cuando sea perturbado. Sin embargo, en el caso de que los valores propios sean iguales y signo opuesto no hay valor propio dominante. En este caso se utilizan las constantes de las condiciones iniciales para determinar la estabilidad.

Otro posible caso dentro de un sistema es cuando el valor propio es 0. Cuando esto ocurre, el sistema permanecerá en la posición a la que está perturbado, y no será impulsado hacia o lejos de su valor de estado estacionario. También es posible que un sistema tenga dos valores propios idénticos. En este caso los dos valores propios idénticos producen solo un vector propio. Debido a esto, puede surgir una situación en la que los valores propios no dan la historia completa del sistema, y se debe utilizar otro método para analizarlo, como el Método de Análisis de Estabilidad de Routh.

Los valores propios también pueden ser números imaginarios complejos o puros. Si se altera el sistema y los valores propios son números no reales, la oscilación se producirá alrededor del valor de estado estacionario. Si el valor propio es imaginario sin ninguna parte real presente, entonces el sistema oscilará con amplitud constante alrededor del valor de estado estacionario. Si es complejo con una parte real positiva, entonces el sistema oscilará con una amplitud creciente alrededor de la función, alejando al sistema cada vez más de su valor de estado estacionario. Por último, si el valor propio es un número complejo con una parte real negativa, entonces el sistema oscilará con amplitud decreciente hasta que finalmente llegue nuevamente a su valor de estado estacionario.

A continuación se muestra una tabla de valores propios y sus efectos sobre un sistema diferencial cuando se altera. Cabe señalar que los valores propios desarrollados para un sistema deben revisarse como un sistema y no como valores individuales. Es decir, los efectos enumerados en la tabla a continuación no representan completamente cómo responderá el sistema. Si pretendieras que los valores propios eran clavos en una tabla Plinko, conocer la ubicación y el ángulo de uno de esos clavos no te permitiría predecir o saber cómo caería el disco Plinko por la pared, porque no sabrías la ubicación o ángulo de los otros clavos. Si tienes información sobre todas las uñas en la tabla Plinko, podrías desarrollar una predicción basada en esa información. Más información sobre el uso de valores propios para el análisis de estabilidad se puede ver aquí, Usando valores propios y vectores propios para encontrar estabilidad y resolver ODES_wiki.

La imagen de arriba es de una tabla de plinko con solo una posición de clavo conocida. Sin conocer la posición de los otros clavos, la caída del disco Plinko por la pared es impredecible.

Conocer la colocación de todos los clavos en esta tabla Plinko permite al jugador conocer los patrones generales que el disco podría seguir.

Valores propios repetidos

Un último caso de interés son los valores propios repetidos. Si bien un sistema de ecuaciones$N$ diferenciales también debe tener$N$ valores propios, estos valores pueden no ser siempre distintos. Por ejemplo, el sistema de ecuaciones:

\ [\ begin {alinear*}
&\ frac {d C_ {A}} {d t} =f_ {A, en}\ rho C_ {A} =f_ {fuera}\ rho C_ {A}\ sqrt {V_ {1}} -V_ {1} k_ {1} C_ {A} C_ {B}\\ [4pt]
y\ frac {d C_ {A}} {d t} = f_ {A} =f_ {A}\ {A}\ ac {d C_ {B}} {d t} =f_ {B, in}\ rho C_ {B in} -f_ {out}\ rho C_ {B}\ sqrt {V_ {1}} -V_ {1} k_ {1} C_ {A} C_ {B}\\ [4pt]
&\ frac {d C_ {C}} d t} =-f_ { out}\ rho C_ {c}\ sqrt {V_ {1}} +V_ {1} k_ {1} C_ {A} C_ {B}\\ [4pt]
&\ frac {d V_ {1}} {d t} =f_ {A, in} +f_ {B, in} -f_ {out}\ sqrt {V_ {1}}\\ [4pt]
&\ frac {d V_ {2}} {d t} =f_ {out}\ sqrt {V_ {1}} -f_ {cliente}\ sqrt {V_ {2}}\\ [4pt]
&\ frac {d C_ {C 2}} {d t} =f_ {\ text {out}},\ rho {C}\ sqrt {V_ {1}} -f_ {\ text {cliente}},\ rho C_ {\ mathrm {C} 2}\ sqrt {V_ {2}}
\ end {align*}\ nonumber\]

Puede producir los valores propios: {-82, -75, -75, -75, -75, -0.66, -0.66}, en los que las raíces '-75' y '-0.66' aparecen varias veces. Los valores propios de repetición llevan más escrutinio en cualquier análisis porque pueden representar un caso de borde, donde el sistema está operando en algún extremo. En términos matemáticos, esto significa que no se pueden generar vectores propios linealmente independientes para completar la base matricial sin más análisis. En términos de ingeniería “del mundo real”, esto significa que un sistema en un caso de borde podría distorsionarse o fallar inesperadamente.

Sin embargo, para la solución general:

\[Y(t)=k_{1} \exp (\lambda t) V_{1}+k_{2} \exp (\lambda t)\left(t V_{1}+V_{2}\right)\nonumber \]

Si$λ < 0$, a medida que$t$ se acerca al infinito, la solución se acerca a 0, lo que indica un sumidero estable, mientras que si λ > 0, la solución se acerca al infinito en el límite, indicando una fuente inestable. Así, las reglas anteriores se pueden aplicar aproximadamente para repetir valores propios, que el sistema sigue siendo probablemente estable si son reales y menores que cero y probablemente inestables si son reales y positivos. Sin embargo, uno debe ser consciente de que un comportamiento inusual es posible. Este curso no se preocupará por el comportamiento resultante de los valores propios repetidos, pero para más información, consulte:

Ejemplo$\PageIndex{1}$

Su supervisor inmediato, el ingeniero sénior Capitán Johnny Goonewadd, le ha llevado a un proyecto que trata con un nuevo sellador a base de silcono que se encuentra en el nivel del suelo de la investigación. Su trabajo es caracterizar la expansión térmica del sellador con el tiempo dado una fuente de alimentación constante. Por suerte, se le dio una serie de ecuaciones diferenciales que relacionan temperatura y volumen en términos entre sí con respecto al tiempo (Nota: T y V son ambos números adimensionales con respecto a sus valores correspondientes en t=0). Resolver el sistema de diferenciales y determinar las ecuaciones tanto para Temperatura como para Volumen en términos de tiempo.

Solución

Se le da la condición inicial en el tiempo t=0, T=1 y V=1

\[\frac{d T}{d t}=4 T-3 V\nonumber \]

\[\frac{d V}{d t}=3 T+4 V\nonumber \]

Al definir una matriz tanto para los coeficientes como para las variables dependientes, podemos reescribir la serie anterior de diferenciales en forma de matriz

\ [A=\ left [\ begin {array} {cc}
4 & -3\\
3 & 4
\ end {array}\ derecha]\ nonumber\]

\ [X=\ left [\ begin {array} {l}
T\\
V
\ end {array}\ derecha]\ nonumber\]

\ [A * X=\ left [\ begin {array} {l}
\ frac {d T} {d V}\
\ frac {d V} {d t}
\ end {array}\ derecha]\ nonumber\]

Lambda se inserta en la matriz A para determinar los valores propios

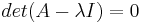
$mathbf {} {det} (A-\ lambda I) =0$

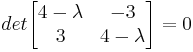
$et\ begin {bmatrix} 4-\ lambda y -3\\ 3 y 4-\ lambda\ end {bmatrix} =0$

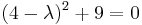
$mathbf {} (4-\ lambda) ^2+9=0$

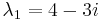
$mathbf {}\ lambda_1=4-3i$

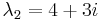
$mathbf {}\ lambda_2=4+3i$

Para cada valor propio, debemos encontrar el vector propio. Empecemos con λ ₁ = 4 − 3 i

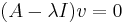
$mathbf {} (A-\ lambda I) v=0$

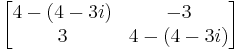
$start {bmatrix} 4- (4-3i) & -3\\ 3 & 4- (4-3i)\ end {bmatrix}$

mathbf {} 3iT - 3V = 0

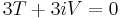
mathbf {} 3T + 3iV = 0

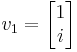
$_1 =\ begin {bmatrix} 1\\ i\ end {bmatrix}$

Ahora encontramos el vector propio para el valor propio λ ₂ = 4 + 3 i

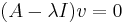
$mathbf {} (A-\ lambda I) v=0$

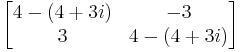
$start {bmatrix} 4- (4+3i) & -3\\ 3 & 4- (4+3i)\ end {bmatrix}$

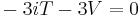
mathbf {} -3iT - 3V = 0

mathbf {} 3T -3iV = 0

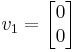
$_1 =\ begin {bmatrix} 0\\ 0\ end {bmatrix}$

La solución general está en la forma

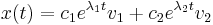
$mathbf {} x (t) =c_1e^ {\ lambda_1 t} v_1 + c_2e^ {\ lambda_2 t} v_2$

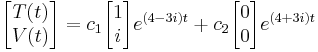
$start {bmatrix} T (t)\\ V (t)\ end {bmatrix} = c_1\ begin {bmatrix} 1\\ i\ end {bmatrix} e^ {(4-3i) t} + c_2\ begin {bmatrix} 0\\ 0\ end {bmatrix} e^ {(4+3i) t}$

$begin {bmatrix} T (t)\\ V (t)\ end {bmatrix} = c_1\ begin {bmatrix} 1\\ i\ end {bmatrix} e^ {(4-3i) t}$

Existe una prueba matemática, la fórmula de Euler, para transformar exponenciales complejos en funciones de pecado (t) y cos (t)

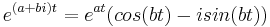
$mathbf {} e^ {(a+bi) t} = e^ {at} (cos (bt) - isin (bt))$

Así

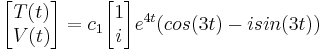
$begin {bmatrix} T (t)\\ V (t)\ end {bmatrix} = c_1\ begin {bmatrix} 1\\ i\ end {bmatrix} e^ {4t} (cos (3t) -isin (3t))$

Simplificando

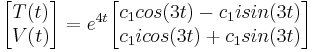
$start {bmatrix} T (t)\\ V (t)\ end {bmatrix} = e^ {4t}\ start {bmatrix} c_1cos (3t) -c_1isin (3t)\\ c_1icos (3t) +c_1sin (3t)\ end {bmatrix}$

Como ya no conocemos el valor de c ₁, hagamos esta ecuación más simple haciendo la siguiente sustitución

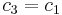
$mathbf {} c_3=c_1$

$mathbf {} c_4=c_1i$

Así, conseguimos tener nuestra solución en términos de números reales

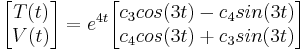
$start {bmatrix} T (t)\\ V (t)\ end {bmatrix} = e^ {4t}\ start {bmatrix} c_3cos (3t) -c_4sin (3t)\\ c_4cos (3t) +c_3sin (3t)\ end {bmatrix}$

O, reescribir la solución en forma escalar

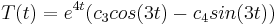
$mathbf {} T (t) = e^ {4t} (c_3cos (3t) -c_4sin (3t))$

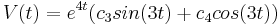
$mathbf {} V (t) = e^ {4t} (c_3sin (3t) +c_4cos (3t))$

Ahora que tenemos nuestras soluciones, podemos usar nuestras condiciones iniciales para encontrar las constantes c ₃ y c ₄

Primera condición inicial: t=0, T=1

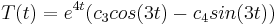
$mathbf {} T (t) = e^ {4t} (c_3cos (3t) -c_4sin (3t))$

$mathbf {} 1 = e^ {4*0} (c_3cos (3*0) -c_4sin (3*0))$

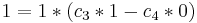
$mathbf {} 1 = 1 * (c_3*1 - c_4 * 0)$

$mathbf {} c_3=1$

Primera condición inicial: t=0, V=1

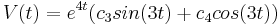
$mathbf {} V (t) = e^ {4t} (c_3sin (3t) +c_4cos (3t))$

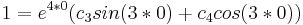
$mathbf {} 1 = e^ {4*0} (c_3sin (3*0) +c_4cos (3*0))$

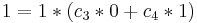
$mathbf {} 1 = 1* (c_3*0 + c_4*1)$

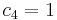
$mathbf {} c_4=1$

Ya hemos llegado a nuestra solución

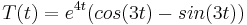
$mathbf {} T (t) = e^ {4t} (cos (3t) -sin (3t))$

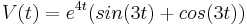
$mathbf {} V (t) = e^ {4t} (sin (3t) +cos (3t))$

Consulte Usar valores propios y vectores propios para encontrar estabilidad y resolver ODES_wiki para resolver ODEs usando los valores propios y vectores propios.

Ejemplo$\PageIndex{2}$

El ingeniero de procesos, Dilbert Pickel, ha comenzado su primer día para la fábrica de salmuera Helman's Pickel. Su primera tarea es con un equipo previo al inicio formulado para poner en marcha una nueva planta diseñada para hacer salmuera de encurtidos agrios grousley. Las limitaciones financieras han exigido que el proceso comience a producir un buen producto lo antes posible. Sin embargo, se ve obligado a reflujo el proceso hasta alcanzar el nivel establecido de acidez. Tienes ecuaciones que relacionan toda la variable de proceso en términos entre sí con respecto al tiempo. Por lo tanto, es trabajo de Dill Pickles caracterizar todas las variables del proceso en términos de tiempo (Acidez adimensional, Acidez y Contenido de Agua; S, A, & W respectivamente). A continuación se muestra el conjunto de diferenciales que se utilizarán para resolver la ecuación.

\ [\\ comenzar {matriz} {l}
\ frac {d S} {d t} =S+A+10 W\
\ frac {d A} {d t} =S+5 A+2 W\
\ frac {d W} {d t} =4 S+3 A+8 W
\ final {matriz}]

Así, la matriz de coeficientes

\ [\ mathbf {A} =\ left [\ begin {array} {lll}
1 & 1 & 10\\
1 & 5 & 2\\
4 & 3 & 8
\ end {array}\ derecha]\ nonumber\]

Usando Mathematica es fácil ingresar los coeficientes del sistema de ecuaciones en una matriz y determinar tanto los valores propios como los vectores propios. 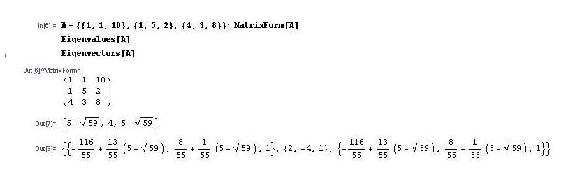athematica eigenvectors3.JPG

Los vectores propios pueden entonces ser utilizados para determinar la solución final al sistema de diferenciales. Algunos puntos de datos serán necesarios para determinar las constantes.

\ [\ left [\ begin {array} {l}
S\\
A\
W
\ end {array}\ right] =C_ {1}\ left [\ begin {array} {c}
0.88\
0.38\\
1
\ end {array}\ right] e^ {(5+\ sqrt {89} k} +C_ {2}\ left [\ begin {array} {c}
2\\
-4\\
1
\ end {array}\ derecha] e^ {4 t} +C_ {3}\ left [\ begin {array} {c}
-2.74\\
0.10\\
1
\ end {array}\ derecha]\ nonumber\]

Consulte Usar valores propios y vectores propios para encontrar estabilidad y resolver ODES_wiki para resolver ODEs usando los valores propios y vectores propios.

Ejemplo$\PageIndex{3}$

Es posible encontrar los valores propios de sistemas más complejos que los mostrados anteriormente. Hacerlo, sin embargo, requiere el uso de herramientas avanzadas de software de manipulación matemática como Mathematica. Utilizando Mathematica, es posible resolver el sistema de ODEs que se muestra a continuación.

\ [\ comenzar {alineado}
\ frac {d X} {d t} &=8 X+\ frac {10 X Y F} {X+Z}\
\ frac {d Y} {d t} &=4 F-Y-Z-\ frac {3 X Y} {X+Y}\
\ frac {d Z} {d t} &=9 X-2 Z+F
\ fin alineado}\ nonumber\]

Obviamente, este sistema de ODEs tiene 4 variables y sólo 3 ecuaciones.

Obviamente, se trata de un conjunto de ODE más complejo que los mostrados anteriormente. Y a pesar de que van a crear un conjunto más complejo de valores propios, se resuelven de la misma manera cuando se utiliza Mathematica.

Usando el código que se muestra a continuación:

igen- Imagen 1.JPG

Las ecuaciones pueden ser ingresadas en Mathematica. Las ecuaciones se muestran de nuevo en la salida

Luego, usando el siguiente bit de código:

igen- Imagen 2.JPG

El es posible encontrar donde las ecuaciones son iguales a 0 (es decir, los puntos fijos). Los resultados de esto también se muestran en la imagen de arriba. Es notable que se encuentran 3 soluciones. Esto tiene sentido ya que el sistema es de 3 ODEs.

El jacobiano se puede encontrar simplemente usando el código que se muestra a continuación.

igen- Imagen 3.JPG

Los ersultos de encontrar al jacobiano se muestran en la ecuación anterior.

Por último, para encontrar uno de los valores propios, uno puede simplemente usar el código que se muestra a continuación.

igen- Imagen 4.JPG

Esto da el Eigenvalue cuando se aplica el primer punto fijo (la primera solución encontrada para “s”). Las otras dos soluciones se podrían encontrar simplemente cambiando la cuchilla fija a la que se hace referencia al encontrar t1. Los otros valores propios no se muestran debido a su gran tamaño.

Ejercicio$\PageIndex{1}$: Calculating Eigenvalues and Eigenvectors using Numerical Software

¿Cuáles son los valores propios para la matriz A?

\ [\ mathbf {A} =\ left [\ begin {array} {cc}
4 & 2\\
3 & -1
\ end {array}\ derecha]\ nonumber\]

$\lambda_{1}=-2$y$\lambda_{1}=5$
$\lambda_{1}=2$y$\lambda_{1}=-5$
$\lambda_{1}=2$y$\lambda_{1}=5$
$\lambda_{1}=-2$y$\lambda_{1}=-5$

Contestar

a. $lambda_1=-2\ qquad\ lambda_2=5$

Ejercicio$\PageIndex{2}$: Using Eigenvalues to Determine Effects of Disturbing a System

Cuando se altera un sistema diferencial con un valor propio negativo real, el sistema es...

Alejado del valor de estado estacionario
Sin cambios y permanece en el valor perturbado
Impulsado de nuevo al valor de estado estacionario
Impredecible y los efectos no se pueden determinar

Contestar: c. Un valor propio negativo real es indicativo de un sistema estable que volverá al valor de estado estacionario después de que sea perturbado.

Referencias

Kravaris, Costas: Control de Procesos Químicos: Un Enfoque en el Dominio del Tiempo. Ann Arbor: La Universidad de Michigan, pp 1-23, A.1-A.7.
Bhatti, M. Asghar: Métodos de optimización práctica con aplicaciones de Mathematica. Springer, pp 75-85, 677-691.
Strang, Prof. Gilbert: “Valores propios y vectores propios”. Matemáticas 18.06. Lord Foundation de Massachusetts. Otoño de 1999.
Edwards, C. Henry y David E. Penney: Ecuaciones Diferenciales: Computación y Modelado. Upper Saddle River: Pearson Education, Inc, pp 299-365.
Teknomo, Kardi. Encontrar el valor Eigen de la matriz simétrica usando Microsoft Excel. http:\\ people.revoledu.com\ kardi\ tutorial\ Excel\ EigenValue.html

Colaboradores y Atribuciones

Autores: (19 de octubre de 2006) Tommy Diraimondo, Rob Carr, Marc Palmer, Matt Pickvet
Administradores: (22 de octubre de 2007) Shoko Asei, Brian Byers, Alexander Eng, Nicholas James, Jeffrey Leto

Search