10.4: Uso de valores propios y vectores propios para encontrar estabilidad y resolver ODEs

Última actualización
Guardar como PDF

Page ID: 85576

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Introducción

Los valores propios y los vectores propios son muy útiles en el modelado de procesos químicos. Al diseñar los controles para un proceso es necesario crear un programa para operar estos controles. En estos programas se utilizan ecuaciones diferenciales para operar los controles con base en variables del sistema. Estas ecuaciones pueden resolverse a mano o mediante el uso de un programa de computadora. Las soluciones para estas ecuaciones diferenciales determinarán la estabilidad del sistema. Después de encontrar esta estabilidad, se puede mostrar si el sistema será estable y amortiguado, inestable y sin amortiguar (para que haya fluctuación constante en el sistema), o como un sistema inestable en el que la amplitud de la fluctuación siempre va en aumento. Para el primer caso, un sistema estable y amortiguado, si hay un cambio, el sistema se ajustará correctamente para volver al estado estacionario. Para los otros dos casos, el sistema no podrá regresar al estado estacionario. Para la situación de no amortiguamiento, la fluctuación constante será dura para el sistema y puede provocar fallas en el equipo. La situación final, con la amplitud cada vez mayor de las fluctuaciones conducirá a un fracaso catastrófico.

Hay un par de formas de desarrollar la ecuación diferencial utilizada para determinar la estabilidad. Primero, se puede crear una ecuación diferencial para guiar el sistema donde las variables son las lecturas de los sensores en el sistema. Un segundo método sería usar datos reales encontrados al ejecutar el sistema. Podrías ajustar una ecuación diferencial a estos datos y usar esa ecuación para determinar la estabilidad.

En esta sección sobre Estabilidad de Autovalores, primero mostraremos cómo usar los valores propios para resolver un sistema de ODEs lineales. A continuación, utilizaremos los valores propios para mostrarnos la estabilidad del sistema. Después de eso, se introducirá otro método para determinar la estabilidad, la prueba de estabilidad de Routh. Para la prueba de estabilidad de Routh, es innecesario calcular los valores propios lo cual es un beneficio ya que a veces eso es difícil. Finalmente, se discutirán las ventajas y desventajas de usar valores propios para evaluar la estabilidad de un sistema.

Resolviendo ODEs

Los valores propios y los vectores propios se pueden utilizar como método para resolver sistemas lineales de ecuaciones diferenciales ordinarias (ODEs). El método es bastante sencillo y no demasiado tedioso para sistemas más pequeños. Consulte el Método Eigenvector Eigenvalue para resolver sistemas a mano y Linealizar ODEs para una revisión de álgebra lineal/matriz jacobiana. Sin embargo, cuando se trata de resolver grandes sistemas de ODEs, por lo general, es mejor usar algún tipo de programa de computadora matemático. Mathematica es un programa que se puede utilizar para resolver sistemas de ecuaciones diferenciales ordinarias cuando hacerlas a mano es simplemente demasiado tedioso. Una vez que uno supera la sintaxis de Mathematica, ¡resolver enormes sistemas de ecuaciones diferenciales lineales ordinarias se convierte en pan comido!

Uso de valores propios para resolver un sistema

Un sistema lineal se resolverá a mano y utilizando la expresión Eigenvalues [] en Mathematica simultáneamente. Tenga en cuenta que, en las entradas de Mathematica a continuación, “In [] :=” no se teclea literalmente en el programa, solo lo que es después de él. La sintaxis que se necesita escribir es la línea que sigue a “In [] =”. El término se usa aquí para demostrar con mayor precisión la codificación en Mathematica. Para encontrar una solución general del sistema lineal de ecuación diferencial ordinaria:

\[\frac{d x}{d t}=4 x+8 y \nonumber \]

\[\frac{d y}{d t}=10 x+2 y \nonumber \]

Primero ponemos el sistema en forma de matriz:

\ [A=\ left [\ begin {array} {l}
\ frac {d x} {d t}\
\ frac {d y} {d t}
\ end {array}\ right] =\ left [\ begin {array} {cc}
4 & 8\
10 & 2
\ end {array}\ derecha]\ left [\ begin {array} {l}
x\\
y
\ fin {matriz}\ derecha]\ nonumber\]

Donde podemos ver que

\ [A=\ left [\ begin {array} {cc}
4 & 8\\
10 & 2
\ end {array}\ right]\ nonumber\]

En mathatica, podemos usar el siguiente código para representar A:

In [1] := MatrixForm [{{4,8}, {10,2}}] Out [1] :=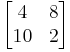

Los valores propios λ ₁ y λ ₂, se encuentran utilizando la ecuación característica de la matriz A, det (A-λI) =0.

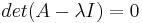
$mathbf {} det (A-\ lambda I) =0$

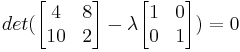
$et (\ begin {bmatrix} 4 & 8\\ 10 & 2\ end {bmatrix} -\ lambda\ begin {bmatrix} 1 & 0\\ 0 & 1\ end {bmatrix}) = 0$

$et\ begin {bmatrix} 4-\ lambda y 8\\ 10 y 2-\ lambda\ end {bmatrix} = 0$

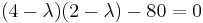
$mathbf {} (4-\ lambda) (2-\ lambda) -80 = 0$

$mathbf {} (\ lambda -12) (\ lambda +6) = 0$

Por lo tanto, λ ₁ = 12 y λ ₂ = − 6

Podemos usar Mathematica para encontrar los valores propios usando el siguiente código:

En [2] := Valores propios [{{4,8}, {10,2}}]

Fuera [2] := {12, -6}

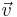Ahora, para cada valor propio (λ ₁ =12 y λ ₂ =-6), se puede encontrar un vector propio asociado con él usando $A-\ lambda I)\ vec {v} = 0$ , donde vec {v} está un vector propio tal que $\ vec {v} =\ lambda\ vec {v}$

i) Para λ ₁ =12

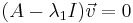
$A-\ lambda_1 I)\ vec {v} = 0$

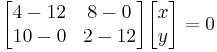
$start {bmatrix} 4-12 & 8-0\\ 10-0 & 2-12\ end {bmatrix}\ start {bmatrix} x\\ y\ end {bmatrix} = 0$

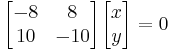
$start {bmatrix} -8 & 8\\ 10 & -10\ end {bmatrix}\ start {bmatrix} x\\ y\ end {bmatrix} = 0$

Esto conducirá a las ecuaciones (1) y (2):

mathbf {} -8x+8y = 0 (1)

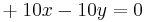mathbf {} +10x-10y = 0 (2)

La entrada de Mathematica es:

En [3] := eqn1= -8x+8y==0
En [4] := eqn2= 10x-10y==0

En [5] := Resolver [{eqn1, eqn2}, {x, y}]

Out[5]:=
Equations (1) & (2) lead to the solution 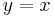mathbf{}y = x

ii) Para λ ₂ =-6,

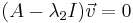
$A-\ lambda_2 I)\ vec {v} = 0$

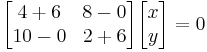
$start {bmatrix} 4+6 & 8-0\\ 10-0 & 2+6\ end {bmatrix}\ start {bmatrix} x\\ y\ end {bmatrix} = 0$

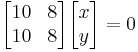
$start {bmatrix} 10 & 8\\ 10 & 8\ end {bmatrix}\ start {bmatrix} x\\ y\ end {bmatrix} = 0$

Esto conducirá a las ecuaciones (3) y (4):

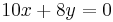mathbf {} 10x+8y = 0 (3)

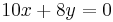mathbf {} 10x+8y = 0 (4)

La entrada de Mathematica es:

En [6] := eqn3= 10x+8y==0
En [7] := eqn4= 10x+8y==0

En [8] := Resolver [{eqn3, eqn4}, {x, y}]

Out[8]:=

Las ecuaciones (3) y (4) conducen a la solución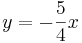 $mathbf {} y = -\ frac {5} {4} x$ .

Recordemos que la dirección de un vector tal como $begin {bmatrix} 1\\ 2\ end {bmatrix}$ es la misma que el vector $comenzar {bmatrix} 4\\ 8\ end {bmatrix}$ o cualquier otro múltiplo escalar. Por lo tanto, para obtener el vector propio, somos libres de elegir ya sea por el valor x o y.

i) Para λ ₁ = 12
Hemos llegado a y = x. Como se mencionó anteriormente, tenemos un grado de libertad para elegir ya sea para x o y Supongamos que x=1. Entonces, y=1 y el vector propio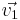 $vec {v_1}$ asociado con el valor propio λ ₁ es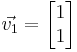 $vec {v_1} =\ begin {bmatrix} 1\\ 1\ end {bmatrix}$

ii) Para λ ₂ = − 6
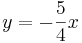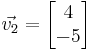Hemos llegado a $=-\ frac {5} {4} x$ . Supongamos que x = 4. Entonces, y = -5 y el vector propio asociado con el valor propio λ ₂ es $vec {v_2} =\ begin {bmatrix} 4\\ -5\ end {bmatrix}$ .

Estos dos autovalores y vectores propios asociados dan la solución:

\ [\ left [\ begin {array} {l}
x (t)\\
y (t)
\ end {array}\ right] =c_ {1}\ left [\ begin {array} {l}
1\\
1
\ end {array}\ right] e^ {12 t} +c_ {2}\ left [\ begin {array} {c}
4\\
-5
\ end {array} derecha] e^ {- 6 t}\ nonumber\]

De ahí que una solución general del sistema lineal en forma escalar es:

\[\begin{align*}{l} x(t)&=c_{1} e^{12 t}+c_{2} 4 e^{-6 t} \\[4pt] y(t)&=c_{1} e^{12 t}-c_{2} 5 e^{-6 t} \end{align*} \nonumber \]

Resolver un sistema usando DSolve

Usando el mismo sistema lineal de ecuaciones diferenciales ordinarias:

\[\frac{d x}{d t}=4 x+8 y \nonumber \]

\[\frac{d y}{d t}=10 x+2 y \nonumber \]

Ingresamos las ecuaciones diferenciales a Mathematica con el siguiente comando:

En: = ODes= {x' [t] ==4x [t] +8y [t], y' [t] ==10x [t] +2y [t]}

donde x' [t] =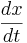 $frac {dx} {dt}$ y y' [t] =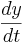 $frac {dy} {dt}$

Después de ingresar las ecuaciones, usamos la función DSolve:

En: = DSolve [ODEs, {x [t], y [t]}, t]

Mathematica generará la solución:

Fuera: =

ParseError: invalid DekiScript (click for details)

Callstack:
    at (Ingenieria/Ingeniería_Industrial_y_de_Sistemas/Libro:_Dinámica_y_Controles_de_Procesos_Químicos_(Woolf)/10:_Análisis_Dinámico_de_Sistemas/10.04:_Uso_de_valores_propios_y_vectores_propios_para_encontrar_estabilidad_y_resolver_ODEs), /content/body/div[2]/div[2]/p[10]/span, line 1, column 1

Este conjunto de ecuaciones, aunque parece más complicado que el primero, en realidad es el mismo.

Estabilidad

Los valores propios se pueden utilizar para determinar si un punto fijo (también conocido como punto de equilibrio) es estable o inestable. Un punto fijo estable es tal que un sistema puede ser perturbado inicialmente alrededor de su punto fijo pero eventualmente regresar a su ubicación original y permanecer allí. Un punto fijo es inestable si no es estable. Para ilustrar este concepto, imagina una bola redonda entre dos colinas. Si se deja sola, la pelota no se moverá, y así su posición se considera un punto fijo. Si tuviéramos que perturbar la pelota empujándola un poco hacia arriba de la colina, la pelota volverá a su posición original entre las dos colinas. Este es un punto fijo estable. Ahora imagina que la pelota está en la cima de una de las colinas. Si se deja inalterado, el balón seguirá permaneciendo en el pico, por lo que esto también se considera un punto fijo. Sin embargo, una perturbación en cualquier dirección hará que la pelota ruede lejos de la cima de la colina. La cima del cerro se considera un punto fijo inestable.

Los valores propios de un sistema linealizado alrededor de un punto fijo pueden determinar el comportamiento de estabilidad de un sistema alrededor del punto fijo. El comportamiento particular de estabilidad depende de la existencia de componentes reales e imaginarios de los valores propios, junto con los signos de los componentes reales y la distinción de sus valores. Examinaremos cada uno de los posibles casos a continuación.

Valores propios imaginarios (o complejos)

Cuando los valores propios son de la forma$a+bi$, donde$a$ y$b$ son escalares reales y$i$ es el número imaginario$\sqrt{-1}$, hay tres casos importantes. Estos tres casos son cuando la parte real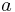 negrita {} a es positiva, negativa y cero. En todos los casos, cuando la parte compleja de un valor propio es distinta de cero, el sistema será oscilatorio.

Parte Real Positiva

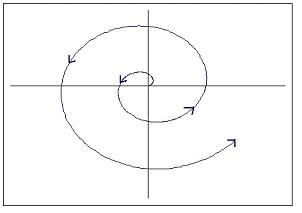
Cuando la parte real es positiva, el sistema es inestable y se comporta como un oscilador inestable. Esto se puede visualizar como un vector que traza una espiral lejos del punto fijo. La gráfica de respuesta con el tiempo de esta situación se vería sinusoidal con amplitud cada vez mayor, como se muestra a continuación.

Esta situación suele ser indeseable cuando se intenta controlar un proceso o unidad. Si hay un cambio en el proceso, derivado del propio proceso o de una perturbación externa, el sistema en sí no volverá al estado estacionario.

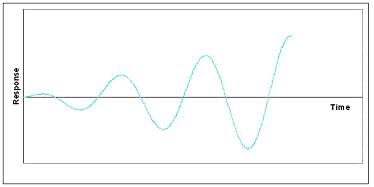Cero Parte Real

Cuando la parte real es cero, el sistema se comporta como un oscilador sin amortiguar. Esto se puede visualizar en dos dimensiones como un vector que traza un círculo alrededor de un punto. La gráfica de respuesta con el tiempo se vería sinusoidal. Las cifras que aparecen a continuación deberían ayudar a comprender.

La oscilación no amortiguada es común en muchos esquemas de control que surgen de controladores competidores y otros factores. Aun así, esto suele ser indeseable y se considera un proceso inestable ya que el sistema no volverá al estado estacionario tras una perturbación.

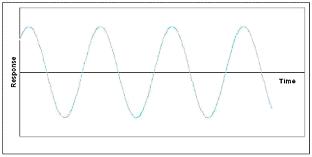Parte Real Negativa

Cuando la parte real es negativa, entonces el sistema es estable y se comporta como un oscilador amortiguado. Esto se puede visualizar como un vector que traza una espiral hacia el punto fijo. La gráfica de respuesta con el tiempo de esta situación se vería sinusoidal con amplitud siempre decreciente, como se muestra a continuación.

Esta situación es lo que generalmente se desea al intentar controlar un proceso o unidad. Este sistema es estable ya que se alcanzará el estado estacionario incluso después de una perturbación en el sistema. La oscilación hará que el sistema vuelva rápidamente al punto de ajuste, pero sobredisparará, por lo que si el exceso es una gran preocupación, se necesitaría una mayor amortiguación.

Al discutir valores propios complejos con partes reales negativas, es importante señalar que tener todas las partes reales negativas de valores propios es una condición necesaria y suficiente de un sistema estable.

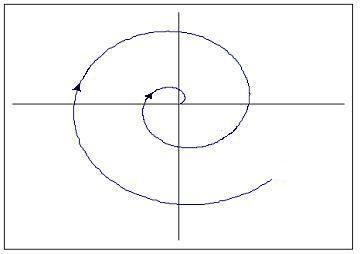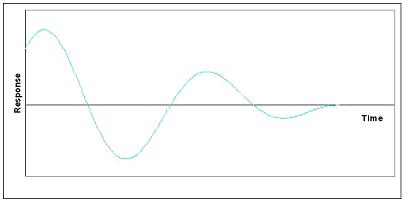Parte compleja de los valores propios

Como se señaló anteriormente, la estabilidad de los sistemas oscilantes (es decir, sistemas con valores propios complejos) se puede determinar enteramente mediante el examen de la parte real. Aunque el signo de la parte compleja del valor propio puede provocar un desplazamiento de fase de la oscilación, la estabilidad no se ve afectada.

Valores propios reales

Hemos visto cómo analizar valores propios que son complejos en forma, ahora veremos valores propios con solo partes reales.

Valores propios cero

Si un valor propio no tiene parte imaginaria y es igual a cero, el sistema será inestable, ya que, como se mencionó anteriormente, un sistema no será estable si sus valores propios tienen partes reales no negativas. Este es solo un caso trivial del complejo valor propio que tiene una parte cero.

Valores propios positivos

Cuando todos los valores propios son reales, positivos y distintos, el sistema es inestable. En un campo degradado, un punto en el campo con múltiples vectores rodeando circularmente y señalando fuera del mismo punto (un nodo) significa todos los valores propios positivos. Esto se llama nodo fuente.

Gráficamente, los valores propios reales y positivos mostrarán una gráfica exponencial típica cuando se grafiquen contra el tiempo.

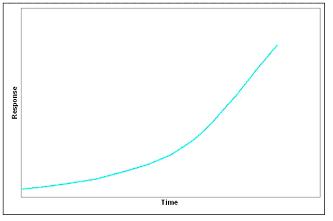
Valores propios negativos

Cuando todos los valores propios son reales, negativos y distintos, el sistema es inestable. Gráficamente en un campo degradado, habrá un nodo con vectores apuntando hacia el punto fijo. Esto se llama nodo sumidero.

Gráficamente, los valores propios reales y negativos generarán una gráfica exponencial inversa.

Valores propios positivos y negativos

Si el conjunto de valores propios para el sistema tiene valores propios positivos y negativos, el punto fijo es un punto de sillín inestable. Un punto de silla de montar es un punto donde una serie de puntos mínimos y máximos convergen en un área en un campo degradado, sin golpear el punto. Se llama punto de sillín porque en la gráfica de superficie tridimensional la función parece un sillín.

Valores propios repetidos

Si el conjunto de valores propios para el sistema tiene valores propios reales repetidos, entonces la estabilidad del punto crítico depende de si los vectores propios asociados con los valores propios son linealmente independientes u ortogonales. Este es el caso de la degeneración, donde más de un vector propio se asocia con un valor propio. En general, la determinación del comportamiento del sistema requiere un mayor análisis. Para el caso de un punto fijo que tenga solo dos valores propios, sin embargo, podemos proporcionar los siguientes dos casos posibles. Si los dos valores propios repetidos son positivos, entonces el punto fijo es una fuente inestable. Si los dos valores propios repetidos son negativos, entonces el punto fijo es un sumidero estable.

Resumen de Gráficas de Valor propio

A continuación se muestra una tabla que resume las representaciones visuales de estabilidad que representan los valores propios.

igenvalue graphs.jpg

Tenga en cuenta que en esta tabla se utilizaron las gráficas de la conferencia de Peter Woolf de Fall'08 titulada Análisis de sistemas dinámicos II: Estabilidad de evaluación, valores propios.

Otro método para determinar la estabilidad

El proceso de encontrar valores propios para un sistema de ecuaciones lineales puede llegar a ser bastante tedioso a veces y para remediarlo, a un matemático británico llamado Edward Routh se le ocurrió un pequeño atajo práctico.

Primero, recordemos que un valor propio inestable tendrá una parte real positiva o cero y que un valor propio estable tendrá una parte real negativa.

La primera prueba es tomar un polinomio de enésimo grado de interés:

\[P(\lambda)=a_{0} \lambda^{n}+a_{1} \lambda^{n-1}+\cdots+a_{n-1} \lambda+a_{n} \nonumber \]

y mira para ver si alguno de los coeficientes es negativo o cero. Si es así, hay al menos un valor con una parte real positiva o cero que se refiere a un nodo inestable.

La forma de probar exactamente cuántas raíces tendrán partes reales positivas o cero es realizando la matriz Routh completa. Refiriéndose al polinomio anterior, funciona de la siguiente manera:

Fila
1	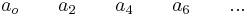$_o\ qquad a_2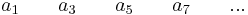\ qquad a_4\ qquad a_6\ qquad...$
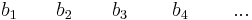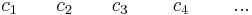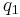2	$_1\ qquad a_3\ qquad a_5\ qquad a_7\ qquad...$
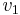3	$_1\ qquad b_2\ qquad b_3\ qquad\; b_4\ qquad\;...$
4	$_1\ qquad c_2\ qquad c_3\ qquad\; c_4\ qquad\;...$
	$vdots\ qquad\ quad\ vdots\ qquad\;\ vdots\;\;\ qquad\ vdots$
n-1	$_1\ qquad p_2$
n	$_1\ qquad$
n+1	$_1\ qquad$

Una matriz de n+1 filas y los coeficientes colocados como arriba. Después de las dos primeras filas, los valores se obtienen de la siguiente manera:

\[b_{1}=\frac{a_{1} a_{2}-a_{0} a_{3}}{a_{1}}, b_{2}=\frac{a_{1} a_{4}-a_{0} a_{5}}{a_{1}}, b_{3}=\frac{a_{1} a_{6}-a_{0} a_{7}}{a_{1}}, \cdots c_{1}=\frac{b_{1} a_{3}-a_{1} b_{2}}{b_{1}}, c_{2}=\frac{b_{1} a_{5}-a_{1} b_{3}}{b_{1}}, c_{3}=\frac{b_{1} a_{7}-a_{1} b_{4}}{b_{1}}, \cdots \nonumber \]

El teorema de Routh dice:

Teorema de Routh

Para que todas las raíces del polinomio sean estables, todos los valores de la primera columna de la matriz Routh deben ser positivos.
Si alguno de los valores de la primera columna es negativo, entonces el número de raíces con una parte real positiva es igual al número de cambios de signo en la primera columna.

Entonces considerando el siguiente ejemplo,

\[f(x)=9 x^{4}+14 x^{3}+7 x+10 \nonumber \]

Prueba preliminar: Todos los coeficientes son positivos, sin embargo, hay un coeficiente cero para x ² por lo que debe haber al menos un punto con una parte real negativa o cero.

Matriz de ruta:

Fila
1	\[\\;9 \qquad \quad 0 \qquad \quad 10 \nonumber \]
2	\[\\; 14 \qquad \; \; 7 \nonumber \]
3	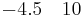$4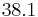.5\ quad 10$
4	$8.1\ qquad$
5	$0\ qquad$

Como la Fila 3 tiene un valor negativo, hay un cambio de signo de Fila 2 a la Fila 3 y nuevamente de la Fila 3 a la Fila 4. Así, hay 2 raíces con parte real positiva o cero.

Resumen de Estabilidad

La siguiente imagen puede funcionar como una referencia rápida para recordar qué campo vectorial resultará dependiendo del valor propio calculado.

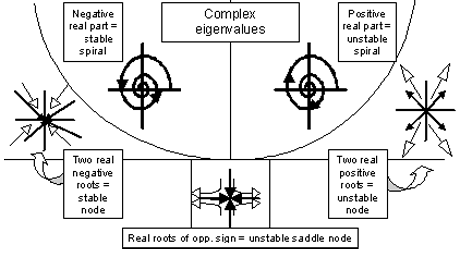
La siguiente tabla da una visión completa de la estabilidad correspondiente a cada tipo de autovalor.

Tipo de valor propio	Estabilidad	Comportamiento Oscilatorio	Notación
Todo Real y +	Inestable	Ninguno	Nodo Inestable
Todo Real y -	Estable	Ninguno	Nodo Estable
Mixtos + & - Real	Inestable	Ninguno	Punto de sillín inestable
+a + b i	Inestable	Sin amortiguar	Espiral inestable
-a + b i	Estable	Damped	Spriral estable
0 + b i	Inestable	Sin amortiguar	Círculo
Valores repetidos	Depende de la ortogonalidad de los vectores propios

Ventajas y desventajas de la estabilidad del valor propio

Existen varias ventajas de usar valores propios para establecer la estabilidad de un proceso en comparación con intentar simular el sistema y observar los resultados. Sin embargo, hay situaciones en las que la estabilidad del valor propio puede descomponerse para algunos modelos.

Ventajas

Alta precisión para sistemas lineales.
Método general que se puede aplicar a una variedad de procesos.
Se puede usar incluso si no se definen todas las variables, como los parámetros de control.

Desventajas

Solo aplicable para modelos lineales.
Las aproximaciones lineales de los modelos no lineales se descomponen del punto fijo de aproximación.

Ejemplo$\PageIndex{1}$

Para el sistema descrito por:

\[\begin{align*} \frac{d x}{d t} &=y \\[4pt] \frac{d y}{d t} &=2 x+y \end{align*} \nonumber \]

Encuentra los puntos fijos y determina su estabilidad.

Solución

Paso 1. Determinar los puntos fijos

En los puntos fijos, nada está cambiando con respecto al tiempo. Por lo tanto, establezca las derivadas a cero para encontrar los puntos fijos.

\ [\ begin {array} {c}
0=y\\
0=2 x+y
\ end {array}\ nonumber\]

Resolviendo estas dos ecuaciones simultáneamente, vemos que tenemos un punto fijo en {0,0}

Paso 2. Determinar el valor propio de este punto fijo

Primero, reescribamos el sistema de diferenciales en forma de matriz.

\ [\ left [\ begin {array} {l}
\ frac {d x} {d t}\
\ frac {d y} {d t}
\ end {array}\ right] =\ left [\ begin {array} {ll}
0 & 1\\
2 & 1
\ end {array}\ right]\ left [\ begin {array} {l}
x\\
\
y { array}\ derecha]\ nonumber\]

A continuación, encuentre los valores propios configurando$\operatorname{det}(A-\lambda I)=0$

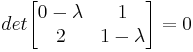
$et\ begin {bmatrix} 0-\ lambda & 1\\ 2 & 1-\ lambda\ end {bmatrix} =0$

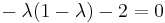
$mathbf {} -\ lambda (1-\ lambda) -2 = 0$

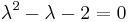
$mathbf {}\ lambda^2-\ lambda-2 = 0$

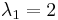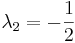
Usando la fórmula cuadrática, encontramos eso $mathbf {}\ lambda_1 = 2$ y $lambda_2 = -\ frac {1} {2}$

Paso 3. Determinar la estabilidad con base en el signo del valor propio

Los valores propios que encontramos fueron números reales. Uno tiene un valor positivo, y otro tiene un valor negativo. Por lo tanto, el punto {0, 0} es un nodo de silla inestable.

La estabilidad se puede observar en la imagen de abajo. El punto fijo se ve en (0,0). Todas las soluciones que no comiencen en (0,0) se alejarán de este punto inestable del sillín. La solución se encontró mediante el uso del sistema bidimensional en pPlane 2005.10 pPlane.

orked out ejemplo1 fase plane.JPG

Ejemplo$\PageIndex{2}$

Determinar la matriz Routh y el número de raíces positivas o cero de la siguiente ecuación.

\[f(x)=6 x^{5}+12 x^{4}+5 x^{3}+3 x^{2}+17 x \nonumber \]

Solución

Matriz Routh:

Fila
1	\[\\;6 \qquad \quad 5 \qquad \quad 17 \nonumber \]
2	\[\\;12 \quad \qquad 3 \qquad \quad 0 \nonumber \]
3	$.5\ qquad 17$
4	$26.1\ qquad$
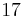5	$7\ qquad$
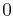6	$\ qquad$

Ya que pasas de un valor positivo en la fila tres, a un valor negativo en la fila cuatro, y de vuelta a un valor positivo en la fila cinco, tendrás una parte real positiva o cero para dos de tus raíces.

Ejemplo$\PageIndex{1}$

Utilice Mathematica para encontrar los valores propios del sistema definidos por:

\ [\ begin {alinear*}
\ frac {d x_ {1}} {d t} &=8 x_ {1} +15 x_ {2} -3 x_ {3} +7 x_ {4} +2 x_ {5}\\ [4pt]
\ frac {d x_ {2}} {d t} &=-22 x_ {1} -21 x_ {2} +3 x_ {3} -12 x_ {4} +11 x_ {5}\\ [4pt]
\ frac {d x_ {3}} {d t} &=10 x_ {1} +6 x_ {2} +24 x_ {3} +3 x_ {4} -6 x_ {5}\\ [4pt]
\ frac {d x_ {4}} {d t} &=0 x_ {1} -2 x_ {2} +21 x_ {3} +0 x_ {4} +4 x_ {5}\\ [4pt]
\ frac {d x_ {5}} {d t} &=4 x_ {1} +9 x_ {2} +x_ {3} -22 x_ {4} -7 x_ {5}
\ final {alinear*}\ nonumber\]

Y comentar sobre la estabilidad de este sistema

Solución

La matriz que corresponde con este sistema es la matriz cuadrada:

\ [\ left [\ begin {array} {ccccc}
8 & 15 & -3 & 7 & 2\\
-22 & -21 & 3 & -12 & 11\\
10 & 6 & 24 & 3 & -6\\
0 & -2 & 21 & 0 & 4\\
4 & 9 & 1 & -22 & -7
\ end {array}\ derecha]\ nonumber\]

Usando la función Eigenvalues [] en Mathematica la entrada es:

En [1] := Valores propios [

ParseError: EOF expected (click for details)

Callstack:
    at (Ingenieria/Ingeniería_Industrial_y_de_Sistemas/Libro:_Dinámica_y_Controles_de_Procesos_Químicos_(Woolf)/10:_Análisis_Dinámico_de_Sistemas/10.04:_Uso_de_valores_propios_y_vectores_propios_para_encontrar_estabilidad_y_resolver_ODEs), /content/body/div[6]/div[2]/div[3]/div/p[8]/span/span, line 1, column 2

]

En [2] := N [%] Este paso produce resultados numéricos

La salida contiene los 5 valores propios:

out [2] := {27.0612, -10.7653 + 10.0084 $i\,$ , -10.7653 - 10.0084 $i\,$ , -0.765272 + 7.71127 $i\,$ , -0.765272 - 7.71127 $i\,$ }

Entonces los cinco valores propios son:

27.0612

-10.7653 + 10.0084 $i\,$

-10.7653 - 10.0084 $i\,$

-0.765272 + 7.71127 $i\,$

-0.765272 - 7.71127 $i\,$

Al observar estos valores propios es claro que el sistema en su conjunto es inestable. Esto se debe a que uno de los valores propios tiene una parte real positiva.

Pregunta de opción múltiple 1

Un sistema es estable si y solo si todos los valores propios del sistema:

a. son reales
b. son complejos
c. tener partes reales negativas
d. tener partes imaginarias negativas

Respuesta: c

Pregunta de opción múltiple 2

¿Qué predicería el siguiente conjunto de valores propios para el comportamiento del sistema?

\[-4,-2+3 i,-2-3 i, 3 \nonumber \]

a. Una oscilación inestable

b. Una oscilación amortiguada

c. Una oscilación sin amortiguar

d. Una fuente

e. Una punta de sillín

Respuesta: d

Referencias

Kravaris, Costas. Control de Procesos Químicos: Un Enfoque en el Dominio del Tiempo.
Liptak, Bela G., Control y Optimización de Procesos. Vol. II. Nueva York: Taylor & Francis.

Colaboradores

Daniel Katzman, Jessica Moreno, Jason Noelanders y Mark Winston-Galant

Search

Parte Real Positiva

Cero Parte Real

Parte Real Negativa

Parte compleja de los valores propios

Valores propios cero

Valores propios positivos

Valores propios negativos

Valores propios positivos y negativos

Teorema de Routh

Ejemplo\(\PageIndex{1}\)

Ejemplo\(\PageIndex{2}\)

Ejemplo\(\PageIndex{1}\)