10.5: Análisis de Plano de Fase - Atractores, Espirales y Ciclos Límite

Introducción a los Atractores, Espirales y Ciclos Límite

A menudo utilizamos ecuaciones diferenciales para modelar un sistema dinámico, como la apertura de una válvula o el llenado de tanques. Sin una fuerza impulsora, los sistemas dinámicos dejarían de moverse. Al mismo tiempo, fuerzas disipativas como la fricción interna y las pérdidas termodinámicas están quitando a la fuerza impulsora. Juntas, las fuerzas opuestas cancelan cualquier interrupción o condición inicial y hacen que el sistema se asiente en un comportamiento típico. Los atractores son la ubicación a la que se atrae el sistema dinámico en su comportamiento típico. Los atractores pueden ser puntos fijos, ciclos límite, espirales u otros conjuntos geométricos.

Los ciclos límite son muy parecidos a fuentes o sumideros, excepto que son trayectorias cerradas más que puntos. Una vez atrapada una trayectoria en un ciclo límite, continuará siguiendo ese ciclo. Por definición, al menos una trayectoria se enrolla en espiral hacia el ciclo límite a medida que el tiempo se acerca al infinito positivo o negativo. Como un sumidero, los ciclos límite atractivos (estables) tienen las trayectorias vecinas acercándose al ciclo límite a medida que el tiempo se acerca al infinito positivo. Como una fuente, los ciclos límite no atractivos (inestables) tienen las trayectorias vecinas acercándose al ciclo límite a medida que el tiempo se acerca al infinito negativo. A continuación se muestra una ilustración de un ciclo límite [1].

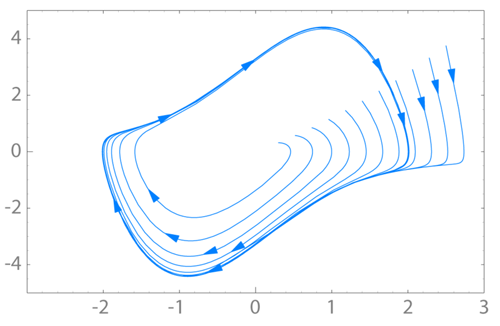
Las espirales son un concepto similar. El atractor es una espiral si tiene valores propios complejos. Si la porción real del valor propio complejo es positiva (es decir, 3 + 2i), el atractor es inestable y el sistema se alejará de la operación en estado estacionario dada una perturbación. Si la porción real del valor propio es negativa (es decir -2 + 5i), el atractor es estable y volverá a la operación en estado estacionario dada una perturbación.

Dado el siguiente conjunto de ecuaciones lineales caminaremos a través de un ejemplo que produce una espiral:

\ [\ comenzar {alinear*}
\ frac {d x} {d t} &=2 x+5 y\
\ frac {d y} {d t} &=-5 x+2 y
\ end {alinear*}\ nonumber\]

La matriz jacobiana serían los coeficientes:

\ [A=\ izquierda|\ begin {array} {cc}
2 & 5\\
-5 & 2
\ end {array}\ derecha|\ nonumber\]

A continuación encontramos los valores propios:

\ [(A-\ lambda I) =\ izquierda|\ begin {array} {cc}
2 & 5\\
-5 & 2
\ end {array}\ derecha|-\ lambda\ izquierda|\ begin {array} {cc}
1 & 0\\
0 & 1
\ end {array}\ derecha|=\ izquierda|\ begin {array} {cc}
(2-\ lambda) & 5\\
-5 & (2-\ lambda)
\ end {array}\ derecha|\ nonumber\]

donde\(I\) esta la matriz de identidad

\ [I =\ izquierda|\ begin {array} {ll}
1 & 0\\
0 & 1
\ end {array}\ derecha|\ nonumber\]

\[\operatorname{det}(A-\lambda I)=(2-\lambda)^{2}+25=0 \nonumber \]

Valores propios:

\[\lambda=2 \pm 5 i \nonumber \]

El sistema es inestable porque la porción real de los valores propios complejos es positiva.

Para encontrar el primer vector propio continuamos enchufando\(2 − 5i\):

\ [\ izquierda|\ begin {array} {cc}
(2-\ lambda) & 5\\
-5 & (2-\ lambda)
\ end {array}\ right|=\ izquierda|\ begin {array} {cc}
2- (2-5 i) & 5\\
-5 & 2- (2-5 i)
\ end {array}\ derecha|=\ izquierda|\ begin {array} {cc}
5 i & 5\ \
-5 y 5 i
\ end {array}\ derecha|\ nonumber\]

\ [(A-\ lambda I) v=\ izquierda|\ begin {array} {cc}
5 i & 5\\
-5 y 5 i
\ end {array}\ derecha| v=0\ nonumber\]

dejar

\[v=\left|\begin{array}{l} x \\ y \end{array}\right| \nonumber \]

\ [\ izquierda|\ begin {array} {cc}
5 i & 5\\
-5 & 5 i
\ end {array}\ derecha|\ izquierda|\ begin {array} {l}
x\\
y
\ end {array} | = |\ begin {array} {l}
0\\
0
\ end {array}\ derecha|\ nonumber\]

Ahora tenemos un sistema de ecuaciones que podemos resolver para x, y:

\ begin {align*}
5 i x+5 y & =0\\
-5 x+5 i y & =0
\ end {alinear*}

Dividiendo ambas ecuaciones por 5:

\ [\ begin {align*}
i x+y & =0\\
-x+i y & =0
\ end {align*}\ nonumber\]

Solución

\ [v_ {1} =\ izquierda|\ begin {array} {c}
-1\\
i
\ end {array}\ derecha|\ nonumber\]

Siguiendo el mismo procedimiento utilizando el segundo valor propio de 2 + 5 i, encontramos que el segundo vector propio es:

\ [v_ {2} =\ izquierda|\ begin {array} {c}
i\\ -1
\ end {array}\ derecha|\ nonumber\]

Ahora enchufando tanto los valores propios como los vectores propios en la ecuación característica:

\ [\ begin {alinear*}
x (t) &=e^ {2 t}\ izquierda (C_ {1}\ cos 5 t+C_ {2}\ sin 5 t\ derecha)\\
y (t) &=e^ {2 t}\ izquierda (C_ {3}\ cos 5 t+C_ {4}\ sin 5 t\ derecha)
\ end {align*}\ nonumber\]

Para más información sobre este procedimiento, consulte: Valores propios y vectores propios

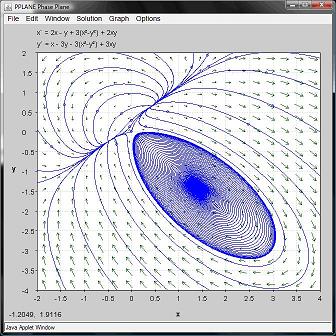
La gráfica fase-plano se muestra a continuación:

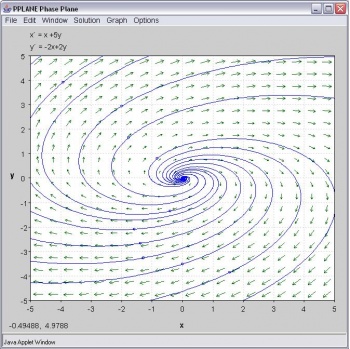
Introducción a Pplane

El análisis de plano de fase es una herramienta importante en el estudio del comportamiento de los sistemas no lineales, ya que a menudo no hay solución analítica para un modelo de sistema no lineal.

PPlane es un applet JAVA para el análisis del plano de fase de sistemas bidimensionales. Comienza en tu navegador web y puedes ingresar directamente tus ecuaciones y valores de parámetros. PPLANE traza campos vectoriales para sistemas de ecuaciones diferenciales. En cada punto, (x, y), de una cuadrícula, PPLANE dibuja una flecha que indica la dirección y magnitud del vector (x', y'). Este vector es igual a dy/dt/dx/dt = dy/dx, y es independiente de t; por lo tanto, debe ser tangente a cualquier curva de solución a través de (x, y).

Permite al usuario trazar curvas de solución en el plano de fase simplemente haciendo clic sobre ellas. También permite al usuario trazar estas soluciones en una variedad de parcelas. Hay una serie de características avanzadas, incluyendo encontrar puntos de equilibrio, valores propios y nullclines, que te resultarán útiles más adelante.

Cómo usar Pplane

En la ventana de ecuación PPlane se puede ingresar un sistema de ecuaciones diferenciales de la forma\(dx/dt = f(x,y)\) y\(dy/dt = g(x,y)\), definir parámetros y cambiar el tamaño de la ventana de visualización. Debajo del menú desplegable Galería, puede cambiar a un sistema lineal.

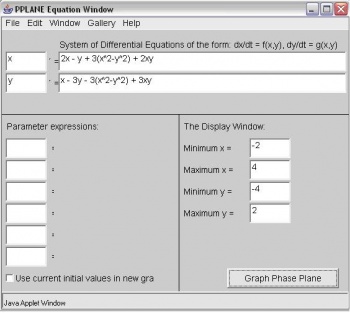
Tenga en cuenta que si sus ecuaciones diferenciales contienen parámetros constantes, puede ingresarlos en los cuadros “Expresiones de parámetros” debajo de las ecuaciones diferenciales como se ve en la siguiente figura (A, B y C se usan como parámetros de ejemplo). Esta es una característica conveniente de usar al considerar el efecto de los parámetros cambiados en el estado estacionario de un sistema porque elimina la redundancia de volver a ingresar los valores de los parámetros varias veces dentro de las ecuaciones diferenciales.

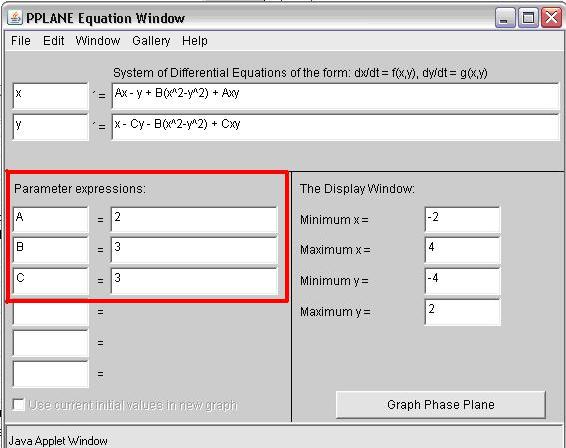
En la ventana pPlane Phase Plane a continuación verá los campos vectoriales para el sistema. Al hacer clic en el campo trazará curvas de solución en el plano de fase. Si está interesado en una gráfica de su solución vs. tiempo o una vista 3D, haga clic en la gráfica:

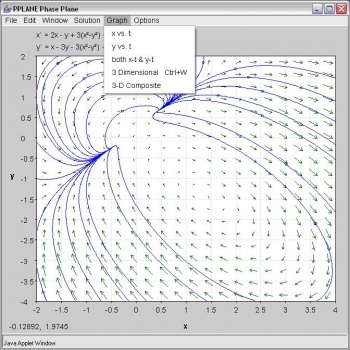
Si elige la opción x-t e y-t, tiene que elegir una curva de solución específica. El resultado se verá así:

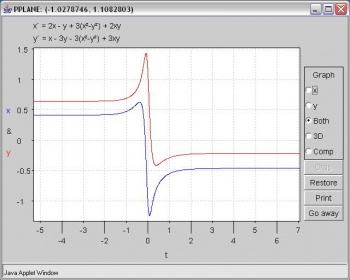
Utilice la función de recorte para acercar un punto de interés

Elija Buscar Punto de Equillibrium en el menú desplegable Solución. Entonces, al hacer clic en una órbita en el plano de fase, la ventana Mensajes Pplane mostrará los valores propios y posibles puntos de equillibrium.

Cosas adicionales que puedes cambiar en PPlane

Cambio del Campo de Talud

Al hacer clic en la pestaña “Opciones”, luego seleccionando “Configuración del campo de dirección”, se puede cambiar el número de filas y columnas trazadas, la forma en que se compone el campo, así como la configuración computacional de PPlane.

Borrando Órbitas Hechas

En la pestaña “Editar”, hay opciones que dicen “Eliminar órbita” o “Eliminar todas las órbitas”. Estas opciones actúan como sus nombres lo implican.

Cambiar la dirección de la gráfica

Al hacer clic en la pestaña “Opciones”, luego seleccionando la opción “Dirección de la solución”, entonces puedes cambiar la forma en que pPlane grafica una línea al hacer clic en el campo. Se puede cambiar la gráfica para trazar hacia adelante (para valores de t>0), hacia atrás (para valores de t<0) o en ambas direcciones de t.

Más usos para PPLAN

De los muchos usos que PPLANE tiene para ofrecer, algunas de las funciones más útiles implican:

Encontrar autovalores/vectores propios para un punto de equilibrio.

Después de graficar una serie de ecuaciones diferenciales, encuentre un punto de equilibrio particular dentro de los datos graficados (“Encontrar un punto de equilibrio”, en la pestaña Solución)

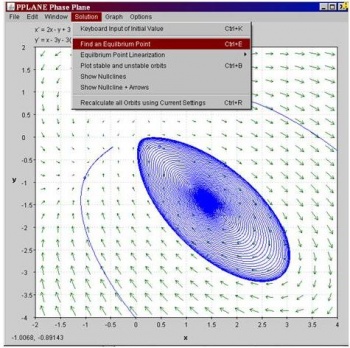
Ahora, al seleccionar un punto en el campo que tenga ben graficado por pplane, pplane encontrará el punto de equilibrio más cercano en la gráfica, y resaltará este punto en la gráfica en rojo.

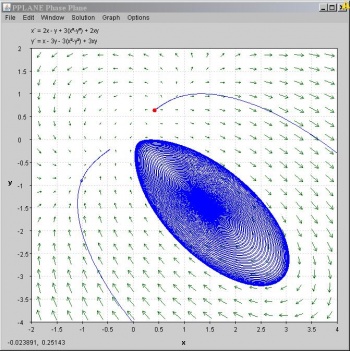
El cuadro Mensajes PPLANE en la esquina superior izquierda de la pantalla debería aparecer con alguna información nueva. Esta información proporciona valores propios y los vectores propios correspondientes al valor de equilibrio seleccionado:

Estabilidad de un Punto de Equilibrio

De manera similar a antes, el Messages Box proporcionará las características de estabilidad (es decir: ¿es un sumidero nodal?) del punto de equilibrio encontrado, inmediatamente después de usar el “Encontrar un punto de equilibrio”.

Otros conceptos de análisis de plano de fase

Separatrix

Una separatriz es cualquier línea en el plano de fase que no es atravesada por ninguna trayectoria. El punto de equilibrio inestable, o punto de silla de montar, a continuación ilustra la idea de una separatriz, ya que ni el eje x ni el eje y están atravesados por una trayectoria. Si te imaginas un mapa topográfico, la seperatriz sería una cresta montañosa; si te caes un poco del borde, nunca volverás. Trazar su plano de fase en Pplane sería útil para identificar puntos de ajuste imposibles, por ejemplo.

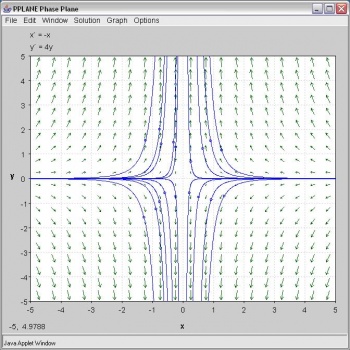
Nullclines

Una nullclina es una curva donde x'=0 o y'=0, indicando así dónde el plano de fase es completamente horizontal o completamente vertical. El punto en el que dos nullclines se cruzan es un punto de equilibrio. Las nullclinas también pueden ser muy útiles para la visualización de un diagrama de plano de fase, ya que dividen el plano de fase en regiones de flujo similar. Para mostrar nullclines en la ventana Plano de fase, seleccione Nullclines en el menú desplegable Soluciones. La captura de pantalla a continuación es un ejemplo.

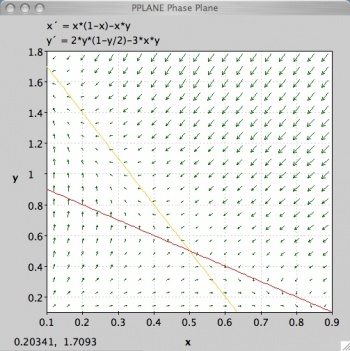
Observe que la nullcline roja muestra donde el flujo es completamente vertical (x'=0) y la nullcline amarilla muestra donde el flujo es completamente horizontal (y'=0).

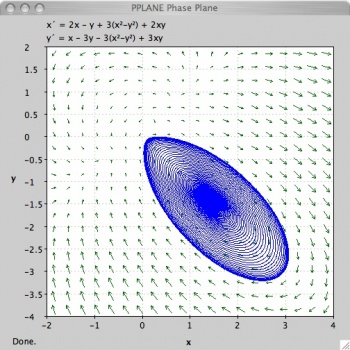
Ciclo límite

A continuación encontrará una curva de solución para un ciclo límite. El ciclo límite contiene la respuesta en un rango establecido, que es algo que puede querer aprovechar para ciertas aplicaciones de ingeniería. Por otro lado siempre está rotando y puede que no sea lo suficientemente estable para tus propósitos.

Tomar capturas de pantalla para copiar retratos de fase Pplane

Con la introducción de Windows Vista, se introdujo la Herramienta de recorte. Esta herramienta permite mucha mayor flexibilidad al tomar capturas de pantalla y editarlas. En este artículo se hablará sobre la Herramienta de recorte así como la tecla Pantalla de impresión de Windows que se puede utilizar para tomar fotos de la pantalla de su computadora. Al presionar la tecla, su computadora copia la imagen de su pantalla y en el portapapeles de su computadora. La imagen puede entonces ser pegada en múltiples programas. Hay muchas instancias a lo largo del curso CHE 466 en las que tomar una captura de pantalla de tu trabajo te será muy útil. Los ejemplos incluyen copiar retratos de fase creados en Pplane, gráficos creados en Mathematica o su código de Mathematica.

Para habilitar la Herramienta de recorte en su computadora Vista, vaya al botón de Windows en la parte inferior izquierda de su pantalla y haga clic en Accesorios -> Herramienta de recorte.

Figura 1. Cómo habilitar la herramienta de recorte

Aparecerá una ventana preguntándole si desea agregar la Herramienta de recorte a su Quicklaunch. Esto proporciona una manera simple y rápida de tomar capturas de pantalla.

Para tomar una foto de tu gráfica, solo tienes que presionar el botón Herramienta de recorte en el área de Inicio rápido y aparecerá una ventana como esta:

Figura 2. La ventana de la herramienta de recorte

Automáticamente, la Herramienta Recortes tendrá por defecto un punto de mira desde el que puedes hacer clic y arrastrar para hacer una selección de la sección de la pantalla que te gustaría representada por un rectángulo rojo.

ADVERTENCIA: En la sección Opciones debes desmarcar “Mostrar tinta de selección después de capturar los recortes” para eliminar el borde rojo alrededor de tus fotos.

Figura 3. Menú de opciones de herramienta de recorte (desmarque la tinta de selección)

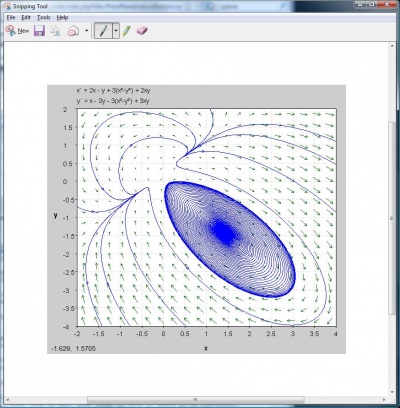
La Herramienta Recortes abrirá una nueva ventana con tu selección y copiará la imagen en tu portapapeles. Siéntase libre de editar su imagen o guardarla donde sea conveniente.

Figura 4. Ventana de edición de herramientas de recorte

Si no usa Windows Vista, aún puede usar Imprimir pantalla:

Siga estos sencillos pasos para copiar y pegar su retrato de fase en un documento de Microsoft Word:

1. Tire hacia arriba de la ventana que contiene su retrato de fase para que se muestre en la pantalla.
2. Encuentra el botón Imprimir Pantalla o PrtSC en la parte superior derecha de tu teclado. (La tecla puede aparecer ligeramente diferente según el fabricante de su teclado de Windows).
3. Abra Microsoft Word al documento de su elección (es decir, CHE 466 Tarea 7).
4. Pegue la imagen en el documento de Word. La figura 1 a continuación indica cómo se verá tu retrato de fase en Word.
5. Para recortar o cambiar el tamaño de la imagen a su gusto, puede usar la barra de herramientas Imagen (que se ve en la Figura 2) seleccionando Ver -> Barras de herramientas -> Imagen.

Si prefieres tomar una captura de pantalla solo de tu retrato de fase en lugar de toda la pantalla de la computadora, sigue estos sencillos pasos:

1. Tire hacia arriba de la ventana que contiene su retrato de fase para que se muestre en la pantalla.
2. Presiona Alt-Print Screen para capturar una foto de la ventana que seleccionaste.
3. Abra Microsoft Word al documento de su elección (es decir, CHE 466 Tarea 7).
4. Pegue la imagen en el documento de Word. La figura 3 a continuación indica cómo se verá tu imagen de retrato de fase.

Figura 5. Captura de pantalla inicial

Figura 6. Documento de Microsoft Word que contiene la captura de pantalla

Figura 7. Captura de pantalla de ventana de retrato de fase

Ejemplo\(\PageIndex{1}\): Linear System of Equations

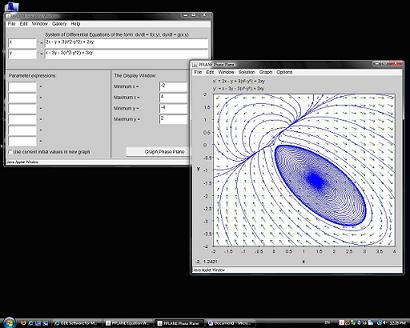
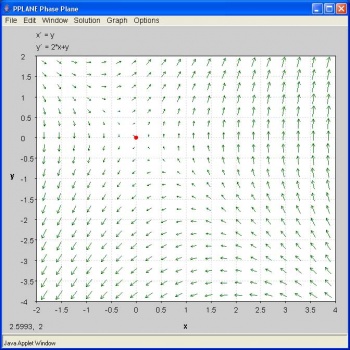
Utilice PPLANE para calcular la siguiente información del sistema que se indica a continuación: ubicación y tipo de punto de equilbrio, matriz jacobiana, vectores propios y valores propios.

\ [\ begin {array} {c}
x^ {\ prime} =y\\
y^ {\ prime} =2 x+y
\ end {array}\ nonumber\]

Solución

Usando la función “Encontrar un Punto de Eculibrium” de PPLANE y haciendo clic en el plano de fase, se indicará el siguiente punto de equilibrio:

La ubicación y el tipo del punto de equilibrio se dan en la ventana “Mensajes PPLANE”, junto con la matriz jacobiana, vectores eigny valores propios.

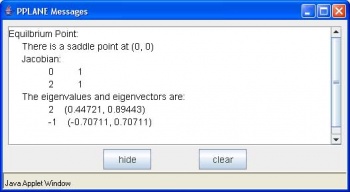
Para nuestro segundo ejemplo de problema nos gustaría que pruebes un sistema no lineal de ecuaciones.

Ejemplo\(\PageIndex{2\): Nonlinear System of Equations

Resuelve para el conjunto de ecuaciones en PPlane. Considerar las tendencias de cambio en la tasa de las ecuaciones diferenciales y posteriormente resolver las ecuaciones en Mathematica para comparar las tendencias. Las siguientes dos ecuaciones diferenciales van a ser utilizadas para recorrer las soluciones en PPlane y Mathematica:

\[\(\frac{d x}{d t}=x-(5 x y) \nonumber \]

\[\frac{d y}{d t}=-2 x+2 y\) \nonumber \]

Solución

Las ecuaciones anteriores se colocaron en la ventana pPlane y se resolvieron. Las dos ventanas siguientes muestran la solución para el conjunto de ecuaciones diferenciales:

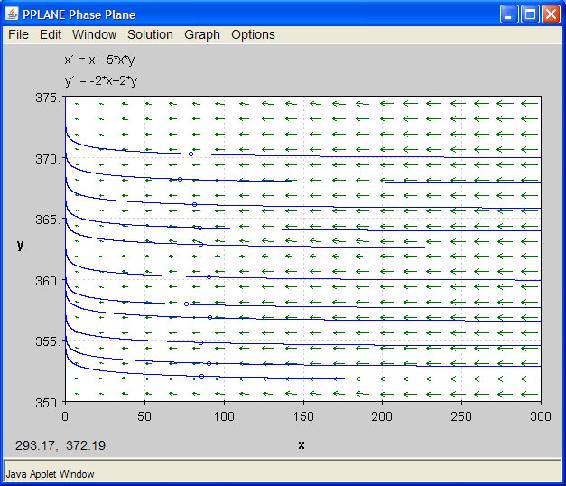
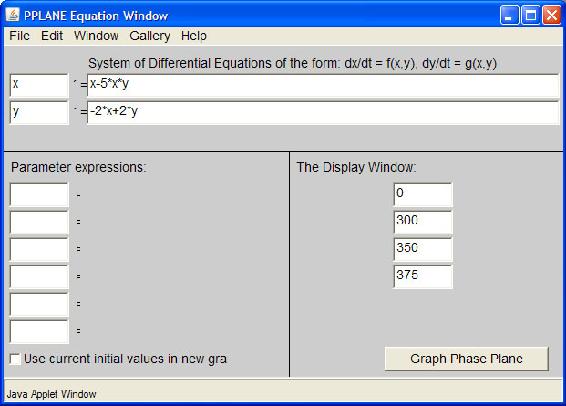
Al observar la gráfica fase-plano, a valores bajos de x e y, t aumenta lentamente. Sin embargo, a valores más altos de y, el incremento en t es rápido. Cuando x es alto e y es bajo, sin embargo, t aumenta lentamente. Mathematica nos ayudará a visualizar mejor las tasas relativas de cambio.

El siguiente es el código utilizado en Mathematica para resolver y trazar el conjunto de ecuaciones diferenciales:

ODEs = {x' [t] == (x [t] - 5*x [t] *y [t]), y' [t] == (-2*x [t]) + (2*y [t]), x [0] == 9, y [0] == 370} NumericalSol = ndSolve [ODEs, {x [t], y [t]}, {t, 1, 100}] Parcela [y [t] /. numericalSol, {t, 1, 100}, PloRange -> Todos]

Las gráficas obtenidas en Mathematica para x versus t e y versus t se muestran a continuación. Tenga en cuenta la diferencia entre las escalas de ejes.

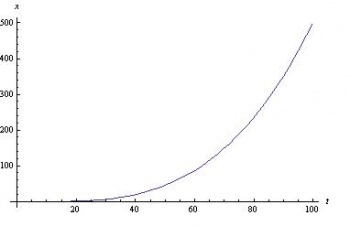
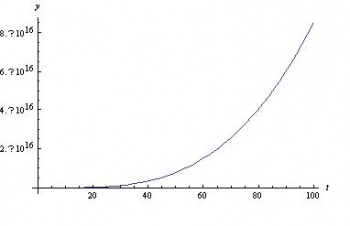
También, para una mirada más cercana, aquí están las parcelas de las pendientes de las gráficas de arriba.

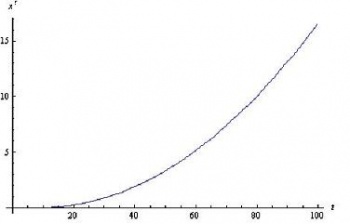
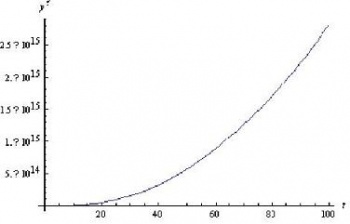
Comparando el incremento en t con el incremento en x, vemos una tendencia similar en el diagrama pPlane. Mathematica muestra un x' en constante aumento con t. A valores más altos de x, el valor para t aumenta en el diagrama pPlane. Sin embargo, como se ve claramente en el diagrama PPlane y las gráficas de la pendiente de x con respecto a t y la pendiente de y con respecto a t, la pendiente de x no se compara con la pendiente muy grande mostrada para y' versus t, por lo que los resultados con Mathematica y PPlane son consistentes.

Este sistema de modelado podría ser utilizado para ver tendencias de variables en un CSTR o cualquier otro sistema que pueda modelarse usando ecuaciones diferenciales.

Preguntas de Opción Múltiple

Pregunta 1

Abra PPLANE e ingrese las siguientes ecuaciones en la Ventana de Ecuaciones PPLANE:

x '= sin (x)

y' = cos (y)

¿Qué aspecto tiene el plano de fase resultante? (Nota: Haga clic en la imagen para agrandar)

A.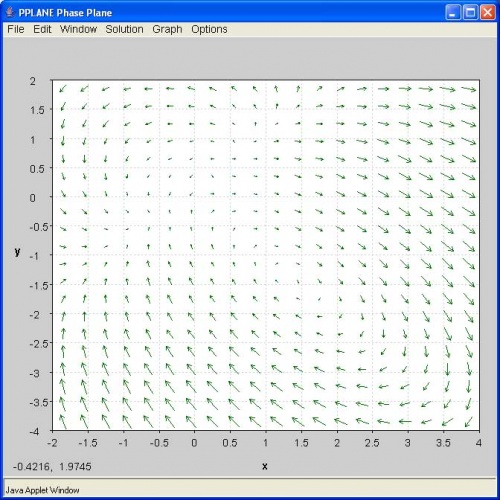

B.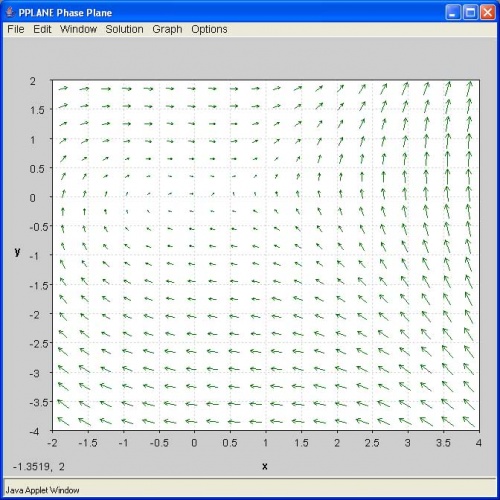

C.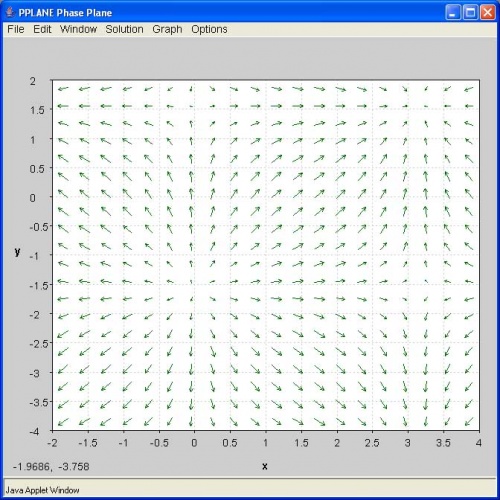

D.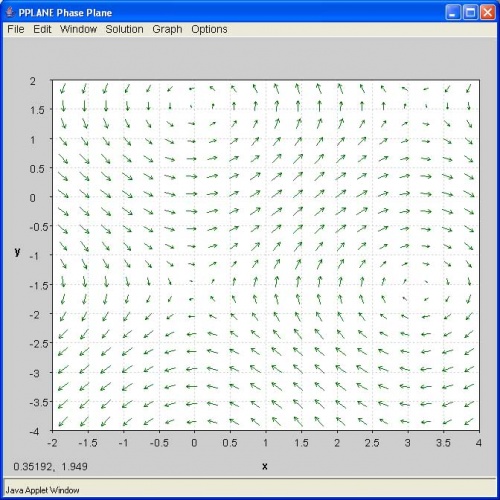

Pregunta 2

Si tiene una perturbación en su sistema y el sistema vuelve al equilibrio, lo más probable es que el valor propio de ese punto fijo sea un:

A. número complejo con componente de número real negativo
B. 0
C. número real negativo
D. número real positivo

Respuestas a las preguntas de opción múltiple

Pregunta 1: C

Pregunta 2: A

Colaboradores y Atribuciones

• Autores: Erin Knight, Dipti Sawalka, Matt Russell, Spencer Yendell
• Administradores: Eric Black, Megan Boekeloo, Daniel Carter, Stacy Young