3.5: Arrastre Usando Conversión de Energía

A continuación, un modelo de caja nos ayudará a estimar las fuerzas de arrastre. Drag, uno de los temas más difíciles de la física, es también una de las fuerzas más importantes en la vida cotidiana. Si no fuera por drag, andar en bicicleta, volar y conducir sería muy fácil. Debido al arrastre, la locomoción requiere energía. El cálculo riguroso de una fuerza de arrastre requiere resolver las ecuaciones Navier-Stokes:

\[(\mathbf{v} \cdot \nabla) \mathbf{v} + \frac{\delta \mathbf{v}}{\delta t} = -\frac{1}{\rho} \nabla p + v \nabla^{2} \mathbf{v}\]

Son ecuaciones acopladas, no lineales, parcial-diferenciales. Se podrían leer muchos volúmenes describiendo las matemáticas para resolver estas ecuaciones. Incluso entonces, las soluciones se conocen solo en unas pocas circunstancias—por ejemplo, una esfera que se mueve lentamente en un fluido viscoso o que se mueve a cualquier velocidad en un fluido no viscoso. Sin embargo, un fluido no viscoso —lo que Feynman [14, Sección II-40-2], citando a John von Neumann, con razón menosprecia como “agua seca”, es particularmente irrelevante para la vida real porque la viscosidad es la causa del arrastre, por lo que una solución de viscosidad cero predice cero arrastre! El uso de un modelo de caja y la conservación de energía es una alternativa simple y perspicaz.

3.5.1 Modelo de caja para arrastre

Primero estimaremos la energía perdida para arrastrar a medida que un objeto se mueve a través de un fluido, como en la Sección 3.2.1. A partir de la energía, encontraremos la fuerza de arrastre. Para cuantificar el problema, imagínese empujar un objeto de área transversal A _cs a velocidad v por una distancia d. El objeto barre un tubo de fluido. (La longitud d del tubo es arbitraria, pero se cancelará fuera de la fuerza).

¿Cuánta energía consume el arrastre?

La energía se consume porque el objeto le da energía cinética al fluido (digamos, agua o aire); viscosidad, como modelaremos en la Sección 6.4.4, luego convierte esta energía en calor. La energía cinética depende de la masa del fluido y de la velocidad que se le dé. La masa de fluido en el tubo es\(\rho A_{cs} d\), donde\(\rho\) está la densidad del fluido. La velocidad impartida al fluido es aproximadamente la velocidad del objeto, que es v. Por lo tanto, la energía cinética dada al fluido es aproximadamente\(\rho A_{cs} v^{2} d\):

\[E_{\textrm{kinetic}} \sim \underbrace{\rho A_{cs} d}_{mass} \times v^{2} = \rho A_{cs} v^{2}d.\]

Este cálculo ignora el factor de la mitad en la definición de energía cinética. Sin embargo, las otras aproximaciones, como suponer que solo se ve afectado el fluido de barrido o que todo el fluido de barrido obtiene velocidad v, son al menos tan inexactas. Para este cálculo aproximado, tiene poco sentido incluir el factor de la mitad.

Esta energía cinética es aproximadamente la energía convertida en calor. Por lo tanto, la energía perdida para arrastrar es más o menos\(\rho A_{cs} v^{2} d\). La fuerza de arrastre viene dada por

\[\underbrace{\textrm{energy lost to drag}}_{\sim \rho A_{cs} v^{2} d} = \underbrace{\textrm{drag force}}_{F_{drag}} \times \underbrace{\textrm{distance}}_{d}.\]

Ahora podemos resolver para la fuerza de arrastre:

\[F_{drag} \sim \rho A_{cs} v^{2}.\]

Como era de esperar, la distancia arbitraria d ha cancelado.

3.5.2 Probar el análisis con un experimento en casa

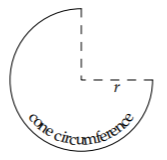
Para probar este análisis, pruebe el siguiente experimento casero. Fotocopie o imprima esta página con una ampliación del 200 por ciento (un factor de 2 mayores en ancho y alto), corte la plantilla y pegue los dos bordes rectos juntos para formar un cono:

Podríamos usar muchas otras formas. Sin embargo, un cono es fácil de construir, y también cae sin balancearse hacia adelante y hacia atrás (como lo haría una hoja de papel) o voltearlo (siempre y cuando lo sueltes hacia abajo).

Probaremos el análisis prediciendo la velocidad terminal del cono: es decir, su velocidad constante al caer. Cuando el cono está cayendo a esta velocidad constante, su aceleración es cero, por lo que la fuerza neta sobre él es, según la segunda ley de Newton, también cero. Así, la fuerza de _{arrastre F drag} es igual al peso mg del cono (donde m es la masa del cono y g es la aceleración gravitacional):

\[\rho_{air} v^{2} A_{cs} \sim mg\]

La velocidad terminal revela así la fuerza de arrastre. (Aunque la fuerza de arrastre es igual al peso, el lado izquierdo es solo una aproximación a la fuerza de arrastre, por lo que conectamos los lados izquierdo y derecho con un solo signo de aproximación ~.) El _término terminal de velocidad v es entonces

\[v_{term} \sim \sqrt{\frac{mg}{A_{cs}\rho_{air}}.}\]

La masa del cono es

\[m = A_{paper} = \underbrace{\textrm{areal density of paper}}_{\sigma_{paper}}.\]

Aquí, Un _papel es el área de la plantilla de cono; y la densidad de área\(\sigma_{paper}\), nombrada en analogía a la densidad regular (volumen), es la masa por área de papel. Aunque la densidad superficial parece una cantidad extraña de definir, se utiliza a nivel mundial para describir el “peso” de diferentes papeles.

El cociente\(m/A_{cs}\) contiene la relación\(A_{paper}/A_{cs}\). En lugar de estimar ambas áreas y encontrar su ratio, estimaremos la relación directamente.

¿Cómo se compara el área transversal A _cs con el área del papel?

¿Cómo se compara el área transversal A _cs con el área del papel?

Debido a que la circunferencia del cono es tres cuartas partes de la circunferencia del círculo completo, su radio de sección transversal es tres cuartas partes del radio r del círculo plantilla. Por lo tanto,

\[A_{cs} = \pi (\frac{3}{4}r)^{2}\]

Debido a que la plantilla es tres cuartas partes de un círculo completo,

\[A_{paper} = \frac{3}{4} \pi r^{2}.\]

El área de papel tiene un factor de tres cuartas partes, mientras que el área de sección transversal tiene dos factores de tres cuartas partes, entonces\(A_{paper}/A_{cs} = 4/3\). Ahora v _término simplifica de la siguiente manera:

\[v_{term} \sim (\frac{\overbrace{A_{paper}\sigma_{paper}}^{m} \times g}{A_{cs} \rho_{air}})^{1/2} = (\frac{\frac{4}{3} \sigma_{paper} g}{\rho_{air}})^{1/2}.\]

El único número desconocido es la densidad de área\(\sigma_{paper}\), la masa por área de papel. Afortunadamente, la densidad de área se usa comercialmente, por lo que la mayoría de las resmas de papel de impresora indican su densidad de área: típicamente, 80 gramos por metro cuadrado.

¿Esto es\(\sigma_{paper}\) consistente con las estimaciones para un billete de dólar en la Sección 1.1?

Allí se estimó que el grosor t de un billete de dólar, o del papel en general, es de aproximadamente 0.01 centímetros. La densidad regular (volumétrica)\(\rho\) sería entonces de 0.8 gramos por centímetro cúbico:

\[\rho_{paper} = \frac{\sigma_{paper}}{t} \approx \frac{80 g m^{-2}}{10^{-2} cm} \times \frac{1m^{2}}{10^{4} cm^{2}} = 0.8 \frac{g}{cm^{3}}.\]

Esta densidad, ligeramente por debajo de la densidad del agua, es una buena suposición para la densidad del papel, que se origina como madera (que apenas flota sobre el agua). Por lo tanto, nuestra estimación en la Sección 1.1 es consistente con la densidad superficial propuesta de 80 gramos por metro cuadrado.

Después de introducir las constantes, se prevé que la velocidad terminal del cono sea aproximadamente 0.9 metros por segundo:

\[v_{term} \sim (\frac{4}{3} \times \frac{\overbrace{8 \times 10^{-2} \textrm{kg m}^{-2}}^{\sigma_{paper}} \times \overbrace{10 \textrm{m s}^{-2}}^{g}}{\underbrace{1.2 \textrm{kg m}^{-3}}_{\rho_{air}}})^{1/2} \sim 0.9 \textrm{m s}^{-1}.\]

Para probar la predicción y, con ella, el análisis que la justifica, sostuve el cono ligeramente por encima de mi cabeza, desde unos 2 metros de altura. Después de soltar el cono, cayó casi exactamente 2 segundos antes de que golpeara el suelo, para una velocidad de aproximadamente 1 metro por segundo, muy cerca de la predicción. ¡Modelos de caja y conservación vuelven a triunfar!

3.5.3 Ciclismo

Al introducir el análisis del drag, dije que el drag es uno de los efectos físicos más importantes en la vida cotidiana. Nuestro análisis del arrastre ahora nos ayudará a comprender la física de una forma de locomoción fantásticamente eficiente: el ciclismo (para su eficiencia, ver Problema 3.34).

¿Cuál es la velocidad de ciclismo récord mundial?

La primera tarea es definir el tipo de récord mundial. Analicemos el ciclismo en terreno nivelado usando una bicicleta normal, aunque es posible velocidades más rápidas en descenso o en bicicletas especiales. En el ciclismo, la energía entra en resistencia a la rodadura, fricción en la cadena y engranajes, y arrastre de aire. La importancia del arrastre aumenta rápidamente con la velocidad, debido al factor de v ² en la fuerza de arrastre, por lo que a velocidades suficientemente altas el arrastre es el consumidor dominante de energía.

Por lo tanto, simplifiquemos el análisis asumiendo que drag es el único consumidor de energía. A la velocidad máxima de ciclismo, la potencia consumida por el arrastre es igual a la potencia máxima que el ciclista puede suministrar. Por lo tanto, el problema se divide en dos estimaciones: la potencia consumida por el _{arrastre (P Drag}) y la potencia que un atleta puede suministrar (P _atleta).

El poder es fuerza por velocidad:

\[\textrm{power} = \frac{\textrm{energy}}{\textrm{time}} = \frac{\textrm{force} \times \textrm{distance}}{\textrm{time}} = \textrm{force} \times \textrm{velocity}\]

Por lo tanto,

\[P_{drag} = F_{drag}v_{max} sim \rho v^{3} A_{cs}.\]

\(P_{drag} = P_{athlete}\)El ajuste nos permite resolver para la velocidad máxima:

\[v_{max} \sim (\frac{P_{athlete}}{\rho_{air}A_{cs}})^{1/3},\]

donde A _cs es el área transversal del ciclista. En la Sección 1.7.2, estimamos P _atleta como 300 vatios. Para estimar el área de la sección transversal, divídala en ancho y alto. El ancho es un ancho de cuerpo, digamos, 0.4 metros. Un ciclista de carreras se agacha, por lo que la altura es de aproximadamente 1 metro en lugar de un total de 2 metros. Entonces A _cs es aproximadamente 0.4 metros cuadrados. El enchufar los números da

\[v_{max} \sim (\frac{300W}{1kg m^{-3}} \times 0.4 m^{2})^{1/3}.\]

Esa fórmula, con su mezcla de vatios, metros y segundos, parece sospechosa. ¿Las unidades son correctas?

Traduzcamos un vatio paso a paso en metros, kilogramos y segundos, usando las definiciones de vatio, julio y newton:

\[W \equiv \frac{J}{s}, \: \: J \equiv NM, \: \: N \equiv \frac{kg m }{s^{2}}.\]

Las tres definiciones se representan en el siguiente árbol de división y conquista, una definición en cada nodo no foliar. Propagar las hojas hacia la raíz nos da la siguiente expresión para el vatio en términos de metros, kilogramos y segundos (las unidades fundamentales en el sistema SI):

\[W \equiv \frac{kg m^{2}}{s^{3}}.\]

Las unidades en v _max se convierten

\[(\frac{\overbrace{\cancel{\textrm{kg m}^{2}} \textrm{ s}^{-3}}^{W}}{\cancel{\textrm{kg }} \textrm{m}^{-3} \times \cancel{m^{2}}})^{1/3} = (\frac{s^{-3}}{m^{-3}})^{1/3}.\]

Los kilogramos cancelan, al igual que los metros cuadrados. La raíz cúbica contiene entonces solo metros en cubos sobre segundos en cubos; por lo tanto, las unidades para v _max son metros por segundo.

Estimemos cuántos metros por segundo. No dejes que la raíz cube te asuste para que uses una calculadora. Podemos hacer la aritmética mentalmente, si masajeamos (ajustamos) los números ligeramente. ¡Si tan solo la potencia fuera de 400 vatios (o en su lugar el área fuera de 0.3 metros cuadrados)! En lugar de desear, hazlo así y no te preocupes por la pérdida de precisión: Debido a que hemos descuidado el coeficiente de arrastre, nuestra velocidad será aproximada de todos modos. Entonces la raíz cubicada se vuelve fácil un cálculo:

\[v_{max} \sim (\frac{\cancel{300} 400W}{1 kg m^{-3} \times 0.4 m^{2}})^{1/3} = (1000)^{1/3} m s^{-1} = 10 m s^{-1}. \]

En unidades más familiares, la velocidad récord es de 22 millas por hora o 36 kilómetros por hora. A modo de comparación, el récord mundial de 1 hora —ciclismo en la medida de lo posible en 1 hora— es de 49.7 kilómetros o 30.9 millas, establecido en 2005 por Ondřej Sosenka. Nuestra predicción, basada en el análisis de conservación de arrastre, es aproximadamente el 70 por ciento del valor real.

¿Cómo puede considerarse útil una estimación de este tipo?

La alta precisión a menudo requiere analizar y rastrear muchos efectos físicos. Los cálculos y la contabilidad pueden ocultar fácilmente el efecto más importante y su idea central, lo que nos cuesta conocimiento y comprensión. Por lo tanto, en casi todas partes de este libro, el objetivo es una estimación dentro de un factor de 2 o 3. Ese nivel de acuerdo suele ser suficiente para convencernos de que nuestro modelo contiene las características esenciales de la situación.

Aquí, nuestra velocidad predicha es solo 30 por ciento menor que el valor real, por lo que nuestro modelo del costo energético del ciclismo debe ser ampliamente correcto. Su principal error surge del factor de la mitad que ignoramos al estimar la fuerza de arrastre, como se puede verificar haciendo Problema 3.33.

3.5.4 Eficiencia de combustible de los automóviles

Las bicicletas, en muchos lugares, son eclipsadas por los autos. A partir del análisis de arrastre, podemos estimar el consumo de combustible de un automóvil (a velocidades de carretera). La mayor parte del mundo mide el consumo de combustible en litros de combustible por cada 100 kilómetros de conducción. Estados Unidos utiliza la cantidad recíproca, la eficiencia de combustible (distancia por volumen de combustible) medida en millas por galón estadounidense. Para desarrollar la flexibilidad de la unidad, haremos el cálculo utilizando ambos sistemas.

Para una bicicleta, comparamos potencias: la potencia consumida por el arrastre con la potencia suministrada por un atleta. Para un automóvil, nos interesa el consumo de combustible, que está relacionado con la energía contenida en el combustible. Por lo tanto, necesitamos comparar energías. Para los autos que viajan a velocidades de carretera, la mayor parte de la energía se consume luchando contra el arrastre. Por lo tanto, la energía consumida por arrastre es igual a la energía suministrada por el combustible.

Conducir una distancia d, que será de 100 kilómetros, consume una energía

\[E_{drag} \sim \rho_{air} v^{2} A_{cs} d.\]

El combustible proporciona una energía

\[E_{fuel} \sim \underbrace{\textrm{energy density}}_{\varepsilon_{fuel}} \times \underbrace{\textrm{fuel mass}}_{\rho_{fuel}V_{fuel}} = \varepsilon_{fuel} \rho_{fuel} V_{fuel}.\]

Porque\(E_{fuel} sim E_{drag}\), el volumen de combustible requerido viene dado por

\[V_{fuel} \sim \frac{E_{drag}}{\rho_{fuel}\varepsilon_{fuel}} \sim \underbrace{\frac{\rho_{air}}{\rho_{fuel}} \frac{v^{2} A_{cs}}{\varepsilon_{fuel}}}_{A_{consumption}} d.\]

Debido a que el lado izquierdo, el _combustible V, es un volumen, el factor complicado frente a la distancia de recorrido d debe ser un área. Hagamos una abstracción nombrando esta área. Debido a que es proporcional al consumo de combustible, un nombre autodocumentante es el _consumo A. Ahora vamos a estimar las cantidades que contiene.

1. Relación de densidad\(\rho_{air}/rho_{fuel}\). La densidad de la gasolina es similar a la densidad del agua, por lo que la relación de densidad es aproximadamente 10−3.

2. Velocidad v. Una velocidad en carretera es de aproximadamente 100 kilómetros por hora (60 millas por hora) o 30 metros por segundo. (Una aproximación útil para los estadounidenses es que 1 metro por segundo es aproximadamente 2 millas por hora).

3. Densidad energética\(\varepsilon_{fuel}\). Estimamos esta cantidad Sección 2.1 como aproximadamente 10 kilocalorías por gramo o 40 megajuolos por kilogramo.

4. Área transversal A _cs. La sección transversal de un automóvil es de aproximadamente 2 metros de ancho por 1.5 metros de altura, por lo que A _cs ∼ 3 metros cuadrados

Con estos valores,

\[A_{consumption} \sim 10^{-3} \times \frac{\overbrace{10^{3} m^{2} s^{-2}}^{v^{2}} \times \overbrace{3 m^{2}}^{A_{cs}}}{\underbrace{4 \times 10^{7} \textrm{J kg} ^{-1}}_{\varepsilon_{fuel}}} \approx 8 \times 10^{-8} m^{2}.\]

Para encontrar el consumo de combustible, que es el volumen de combustible por cada 100 kilómetros de conducción, simplemente multiplique el _consumo de A por d = 100 kilómetros o 10 ⁵ metros, y luego convertir a litros para obtener 8 litros por cada 100 kilómetros:

\[V_{fuel} \approx \underbrace{8 \times 10^{-8} \cancel{m^{2}}}_{A_{consumption}} \times \underbrace{10^{5} \cancel{m}}_{d} \times \frac{10^{3}l}{1 \cancel{m^{3}}} = 8 l.\]

Para la eficiencia de combustible, utilizamos el _consumo A en la forma\(d= V_{fuel}/A_{consumption}\) para encontrar la distancia recorrida en 1 galón de combustible, convirtiendo el galón a metros cúbicos:

\[d \sim \frac{\overbrace{1 \cancel{\textrm{ gallon}}}^{V_{fuel}}}{\underbrace{8 \times 10^{-8} \cancel{m^{2}}_{A_{consumption}}} \times \frac{4 \cancel{l}}{1 \cancel{\textrm{ gallon}}} \times \frac{10^{-3} m^{\cancel{3}}}{1 \cancel{l}} = 5 \times 10^{4} m.\]

El exponente de paso de 3 en el\(m^{\cancel{3}}\) indica que los metros cúbicos se convirtieron en metros lineales, como resultado de la cancelación con el m ² en el _consumo de A. La distancia resultante es de 50 kilómetros o 30 millas. Por lo tanto, la eficiencia de combustible prevista es de aproximadamente 30 millas por galón.

Esta predicción está muy cerca de los valores oficiales. Por ejemplo, para los autos estadounidenses nuevos de tamaño mediano (en 2013), las eficiencias de combustible de los vehículos no eléctricos oscilan entre 16 y 43 millas por galón, con una media y mediana de 30 millas por galón (7.8 litros por 100 kilómetros)

Las predicciones de eficiencia de combustible y consumo de combustible son mucho más precisas de lo que merecemos, ¡dadas las muchas aproximaciones! Por ejemplo, ignoramos todas las pérdidas de energía excepto la resistencia al arrastre. También se utilizó una fuerza de arrastre muy áspera\(\rho_{air}v^{2}A_{cs}\), derivada de un argumento de conservación razonable pero crudo. Sin embargo, como Pippi Calzas-Largas, salimos bien de todos modos.

¿Qué salió bien?

El análisis descuida dos factores importantes, por lo que dicha precisión solo es posible si estos factores se cancelan. El primer factor es la constante adimensional oculta en el signo de aproximación simple de la fuerza de arrastre:

\[F_{drag} \sim \rho_{air} A_{cs}v^{2}.\]

Incluyendo el prefactor adimensional (mostrado en gris), la fuerza de arrastre es

\[F_{drag} = \frac{1}{2}c_{d} \rho_{air}A_{cs} v^{2},\]

donde c _d es el coeficiente de arrastre (introducido en la Sección 3.2.1). El factor de la mitad proviene de la mitad en la definición de energía cinética. El coeficiente de arrastre es el ajuste restante, y su origen es el tema de la Sección 5.3.2. Por ahora, solo necesitamos saber eso, para un auto típico, c _d ≈ 1/2. Por lo tanto, el prefactor adimensional oculto en el signo de aproximación simple es aproximadamente 1/4.

Con base en esta fuerza de arrastre más precisa, ¿los autos usarán más o menos de 8 litros de combustible por cada 100 kilómetros?

Incluyendo el c _d /2 reduce la fuerza de arrastre y el consumo de combustible en un factor de 4. Por lo tanto, los autos viajarían 120 millas con 1 galón de combustible o consumirían solo 2 litros por cada 100 kilómetros. Esta predicción más cuidadosa es demasiado optimista, y mucho peor que la estimación original y más simple.

¿Qué otro efecto descuidamos?

La eficiencia del motor, un motor de combustión típico, ya sea gasolina o humano, es solo aproximadamente 25 por ciento eficiente: Un motor extrae solo una cuarta parte de la energía de combustión en el combustible; las tres cuartas partes restantes se convierten en calor sin hacer trabajo mecánico. Incluyendo este factor aumenta nuestra estimación del consumo de combustible en un factor de 4.

La eficiencia del motor y la fuerza de arrastre más precisa en conjunto dan la siguiente estimación del consumo de combustible, con el nuevo efecto en gris:

\[V_{fuel} \approx \frac{\frac{1}{2}c_{d}}{0.25} \times \frac{\rho_{air}v^{2}A_{cs}}{\rho_{fuel}\varepsilon_{fuel}}d.\]

El 0.25 en el denominador, a partir de la eficiencia del motor, cancela el\(\frac{1}{2}c_{d}\) en el numerador. Es por ello que nuestra estimación despreocupada, que descuidó ambos factores, fue tan precisa. La moral, que pretendo sólo a medias en broma: descuida muchos factores, para que los errores puedan anularse unos a otros.

Ejercicio\(\PageIndex{1}\): Adjusting the cycling record

Nuestra estimación del récord mundial de 1 hora como aproximadamente 35 kilómetros (Sección 3.5.3) ignoró el coeficiente de arrastre. Para un ciclista,\(c_{d} \approx 1\). ¿Incluir el coeficiente de arrastre mejorará o empeorará la predicción en comparación con el récord mundial real (aproximadamente 50 kilómetros)? ¡Responde esa pregunta antes de hacer la nueva predicción! ¿Cuál es la predicción revisada?

Ejercicio\(\PageIndex{2}\): Bicyclist fuel efficiency

¿Cuál es el consumo de combustible y la eficiencia de un ciclista alimentado con mantequilla de maní? Exprese su estimación como eficiencia (millas por galón de mantequilla de maní) y un consumo (litros de mantequilla de maní por cada 100 kilómetros). ¿Cómo se compara una bicicleta con un automóvil?