5.1: Grupos adimensionales

Debido a que las cantidades adimensionales son las únicas cantidades significativas, podemos entender mejor el mundo describiéndolo en términos de cantidades adimensionales. Pero tenemos que encontrarlos.

5.1.1 Encontrar grupos adimensionales

Para ilustrar la búsqueda de estas cantidades adimensionales, probemos un ejemplo que usa la física familiar: Al aprender una nueva idea, es útil probarla en un ejemplo familiar. Encontraremos la aceleración hacia adentro de un tren a medida que se mueve en una vía curva. Cuanto mayor sea la aceleración, más necesita inclinarse la vía o el tren para que los pasajeros no se sientan incómodos y (si la vía no está lo suficientemente inclinada) el tren no vuelca

Nuestro objetivo es la relación entre la aceleración del tren a, su velocidad v, y el radio de curvatura de la vía r. En nuestro estado de conocimiento ahora, la relación podría ser casi cualquier cosa. Aquí hay algunas posibilidades:

\[\frac{a+ v^{2}}{r} = \frac{v^{3}}{a}; \: \frac{r+a^{2}}{v}= \frac{a^{2}}{v + r}; \: \frac{v}{ra + v^{3}}= \frac{a+v}{r^{2}}.\]

Si bien esas posibilidades son falsas, entre el vasto mar de posibles relaciones, una relación es correcta.

Para encontrar la restricción que encogerá el mar a unas gotas, primero desenfocar nuestros ojos y ver todas las opciones como ejemplos de la forma general

A pesar de que las blobs pueden ser funciones complicadas, deben tener dimensiones idénticas. Al dividir ambos lados por la mancha B, obtenemos una forma más simple:

Ahora cada lado es adimensional. Por lo tanto, cualquiera que sea la relación entre a, v y r, podemos escribirla en forma adimensional.

El proceso anterior no se limita a este problema. En cualquier ecuación válida, todos los términos tienen dimensiones idénticas. Por ejemplo, aquí está la energía total en un sistema de muelle—masa:

\[E_{total} = \frac{1}{2} mv^{2} + \frac{1}{2} k x^{2}.\]

El término cinético-energía (mv ² /2) y el término potencial-energía (kx ² /2) tienen las mismas dimensiones (de energía). El mismo proceso de dividir por uno de los términos convierte cualquier ecuación en una ecuación adimensional. Como resultado, cualquier ecuación se puede escribir en forma adimensional. Debido a que las formas adimensionales son una pequeña fracción de todas las formas posibles, esta restricción nos ofrece una enorme reducción en la complejidad.

Para beneficiarnos de esta reducción, debemos describir de manera compacta todas estas formas: Cualquier forma adimensional puede construirse a partir de grupos adimensionales. Un grupo adimensional es el producto de las cantidades, cada una elevada a una potencia, de tal manera que el producto no tiene dimensiones. En nuestro ejemplo, donde las cantidades son a, v y r, cualquier grupo adimensional G tiene la forma

\[G \equiv a^{x}n^{y}r^{z},\]

donde G no tiene dimensiones y donde los exponentes x, y y z son números reales (posiblemente negativos o cero).

Debido a que cualquier ecuación que describa el mundo se puede escribir en forma adimensional, y debido a que cualquier forma adimensional se puede escribir usando grupos adimensionales, cualquier ecuación que describa el mundo se puede escribir usando grupos adimensionales.

Esa noticia es bienvenida, pero ¿cómo encontramos a estos grupos?

a	LT ^-2	aceleración
v	LT ^-1	velocidad
r	L	radio

El primer paso es tabular las cantidades con su descripción y dimensiones. Por convención, se utilizan letras mayúsculas para representar dimensiones. Por ahora, las dimensiones posibles son longitud (L), masa (M) y tiempo (T). Entonces, por ejemplo, las dimensiones de v son longitud por tiempo o de manera más compacta, LT ^-1.

Entonces, al mirar la mesa, encontramos todos los grupos adimensionales posibles. Un grupo adimensional no contiene dimensiones de longitud, masa o tiempo. Para nuestro ejemplo, comencemos por deshacernos de la dimensión del tiempo. Ocurre en a como T ⁻² y en v como T ⁻¹. Por lo tanto, cualquier grupo adimensional debe contener un/v ². Este cociente tiene dimensiones de L ⁻¹. Para hacerlo adimensional, multiplíquelo por la única cantidad que es puramente una longitud, que es el radio r. El resultado, ar/v ², es un grupo adimensional. En la forma a ^x v ^y r ^z, es un ¹ v ^-2 r ¹.

¿Hay otros grupos adimensionales?

Para deshacernos del tiempo, empezamos con un/v ² y luego terminamos, inevitablemente, con el grupo ar/v ². Para hacer otro grupo adimensional, tendríamos que elegir otro punto de partida. Sin embargo, los únicos puntos de partida que se deshacen del tiempo son los poderes de a/v ² —por ejemplo, v ²/a o a ²/v ⁴ — y esas elecciones conducen al poder correspondiente de ar /v ². Por lo tanto, cualquier grupo adimensional se puede formar a partir de ar/v ². Nuestras tres cantidades a, r y v producen exactamente un grupo adimensional independiente.

Como resultado, cualquier declaración sobre la aceleración circular puede escribirse usando solo ar/v ². Todas las declaraciones adimensionales que usan solo ar/v ² tienen la forma general

\[\frac{ar}{v^{2}}=\textrm{dimensionless constant,}\]

porque no hay otros grupos adimensionales independientes para usar en el lado derecho.

¿Por qué no podemos usar ar/v ² en el lado derecho?

Podemos, pero no crea nuevas posibilidades. Como ejemplo, probemos la siguiente forma adimensional:

\[\frac{ar}{v^{2}} =3(\frac{ar}{v^{2}})-1.\]

Su solución es ar/v ² =1/2, que es otro ejemplo de nuestra forma general

\[\frac{ar}{v^{2}}=\textrm{dimensionless constant.}\]

Pero, ¿y si usamos una función más complicada?

Vamos a probar uno:

\[\frac{ar}{v^{2}}=(\frac{ar}{v^{2}})^{2}-1.\]

Sus soluciones son

\[\frac{ar}{v^{2}}=\left \{ \begin{array}{ll} \phi \\-1/\phi, \\ \end{array} \right. \]

donde\(\phi\) está la relación áurea (1.618...). Decidir entre estas soluciones requeriría información o requisitos adicionales, como la convención de signos para la aceleración. Aun así, cada solución es otro ejemplo de la forma general

\[\frac{ar}{v^{2}}=\textrm{dimensionless constant.}\]

Usando esa forma, de la que no podemos escapar, la aceleración del tren es

\[a \sim \frac{v^{2}}{r}\]

donde el ~ contiene la constante adimensional (desconocida). En este caso, la constante adimensional es 1. Sin embargo, el análisis dimensional, como se llama a este procedimiento, no nos dice su valor, que provendría de un análisis de cálculo o, aproximadamente, de un análisis de agrupamiento (Sección 6.3.4).

Usando un ~ v ²/r, ahora podemos estimar la aceleración hacia adentro del tren dando la vuelta a una curva. Imagínese un tren de velocidad moderada viajando a v ≈ 60 metros por segundo (aproximadamente 220 kilómetros o 135 millas por hora). A tales velocidades, los ingenieros ferroviarios especifican que el radio de curvatura de la vía sea de al menos 2 o 3 kilómetros. Usando el radio de curvatura más pequeño, la aceleración hacia adentro se convierte

\[a \sim \frac{(60 m s^{-1})^{2}}{2 \times 10^{3}m} = 1.8 m s^{-2}.\]

Debido a que ninguna cantidad con dimensiones es grande o pequeña por sí sola, esta aceleración por sí misma carece de sentido. Adquiere sentido en comparación con una aceleración relevante: la aceleración gravitacional g. Para este tren, la relación adimensional a/g es de aproximadamente 0.18. Esta relación también es tan θ, donde θ es la inclinación del tren que haría que los pasajeros sintieran una fuerza neta perpendicular al piso. Con un/g ≈ 0.18, el ángulo de inclinación cómodo es de aproximadamente 10 ^°. En efecto, los trenes basculantes pueden inclinarse hasta 8 ^°. (Este rango suele ser suficiente, ya que una inclinación completa es desconcertante: Uno vería un suelo inclinado pero aún sentiría la gravedad actuando como lo hace normalmente, a lo largo del eje del cuerpo).

Usando nuestra fórmula para la aceleración circular, también podemos estimar la velocidad máxima de marcha. Al caminar, un pie siempre está en contacto con el suelo. Como modelo rudo de caminar, todo el cuerpo, representado como una masa puntual en su centro de masa (CM), gira alrededor del pie en contacto con el suelo, como si el cuerpo fuera un péndulo invertido. Si caminas a velocidad v y tienes longitud de pierna l, entonces la aceleración circular resultante (la aceleración hacia el pie) es v ² /l. Cuando caminas lo suficientemente rápido como para que esta aceleración sea superior a g, la gravedad no puede suministrar suficiente aceleración.

Este cambio ocurre cuando\(v \sim \sqrt{gl}\) Entonces tu pie sale del suelo, y la caminata se convierte en una carrera. Por lo tanto, la marcha está determinada por la relación adimensional v ²/gl. Esta relación, que también determina la velocidad de las olas de agua (Problema 5.15) y de los barcos (Problema 5.64), se llama el número Froude y se abrevia Fr.

Aquí hay tres formas de verificar si nuestro modelo de péndulo de caminar es razonable. Primero, la fórmula resultante,

\[v_{max} \sim \sqrt{gl}\]

explica por qué las personas altas, con una longitud de pierna más larga, generalmente caminan más rápido que las personas bajas.

Segundo, predice una velocidad máxima razonable para caminar. Con una longitud de pierna de l ~ 1 metro, el límite es de 3 metros por segundo o aproximadamente 7 millas por hora:

\[v_{max} \sim \sqrt{10 m s^{-2} \times 1m} \approx 3 m s^{-1}.\]

Esta predicción es consistente con las velocidades de carrera récord mundial, donde la puntera trasera puede no abandonar el suelo hasta que el talón delantero haya tocado el suelo. Los récords mundiales de carrera de 20 kilómetros son 1h:24m:50s para mujeres y 1h:17m:16s para hombres. Las velocidades correspondientes son 3.9 y 4.3 metros por segundo.

La tercera prueba se basa en la marcha. En un experimento fascinante, Rodger Kram y sus colegas [31] redujeron la gravedad efectiva g. Esta reducción cambió la velocidad de la transición caminar-correr, pero la velocidad aún satisfizo v ²/gl ~ 0.5. ¡El universo solo se preocupa por las cantidades adimensionales!

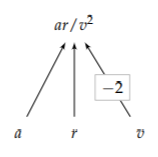
Otra moraleja de esta introducción al análisis dimensional es que cada grupo adimensional es una abstracción. Aquí, el grupo ar/v ² nos dice que el universo se preocupa por a, r, o v a través de la combinación ar/v ². Esta relación es descrita por el diagrama de árbol (la etiqueta de borde de -2 es el exponente de v en v ^-2). Debido a que solo hay un grupo adimensional independiente, al universo solo le importa ar/v ². Por lo tanto, el universo se preocupa por a, r, y v solo a través de la combinación ar/v ². Esta libertad para no preocuparnos por cantidades individuales simplifica nuestra imagen del mundo.

5.1.2 Contando grupos adimensionales

Encontrar la aceleración circular requirió encontrar todos los grupos adimensionales posibles y mostrar que todos los grupos podrían construirse a partir de un grupo, digamos, ar/v ². Ese razonamiento siguió una cadena de restricciones: Para deshacerse del tiempo, el grupo adimensional tenía que contener el cociente a/v ²; para deshacerse de la longitud, el cociente necesitaba ser multiplicado por la potencia correcta de r.

Para cada problema, ¿tenemos que construir una cadena de razonamiento similar para contar los grupos adimensionales?

Seguir las restricciones es útil para encontrar grupos adimensionales, pero hay un atajo para contar grupos adimensionales independientes. El número de grupos independientes es, aproximadamente, el número de cantidades menos el número de dimensiones. Una declaración más precisa vendrá después, pero esta versión es suficiente para que empecemos.

Vamos a probarlo usando el ejemplo de aceleración. Hay tres cantidades: a, v y r. Hay dos dimensiones: longitud (L) y tiempo (T). Debe haber, y hay, un grupo adimensional independiente.

Probemos también el atajo en una fórmula física familiar: W=Mg, donde W es el peso de un objeto, m es su masa y g es la aceleración gravitacional. Hay tres cantidades (W, m y g) hechas de tres dimensiones (M, L y T). Nuestro atajo predice que no hay grupos adimensionales en absoluto. Sin embargo, W/mg es adimensional, ¡lo que refuta la predicción!

W	MLT ^-2	peso
m	M	masa
g	LT ^-2	gravedad

¿Qué salió mal?

Aunque las tres cantidades parecen contener tres dimensiones, las combinaciones tridimensionales realmente utilizadas —fuerza (MLT ⁻²), masa (M) y aceleración (LT ⁻² )— se pueden construir a partir de solo dos dimensiones. Por ejemplo, podemos construirlos a partir de masa y aceleración.

Pero la aceleración no es una dimensión fundamental, entonces, ¿cómo podemos usarla?

La noción de dimensiones fundamentales es una convención humana, parte de nuestro sistema de medición. El análisis dimensional, sin embargo, es un proceso matemático. No le importa ni el universo ni nuestras convenciones para describir el universo. Esa falta de atención puede parecer desalmada y parecer una desventaja. Sin embargo, significa que el análisis dimensional es independiente de nuestras elecciones arbitrarias, dándole poder y generalidad.

En lo que respecta al análisis dimensional, podemos elegir cualquier conjunto de dimensiones como nuestras dimensiones fundamentales. El único requisito es que sean suficientes para describir las dimensiones de nuestras cantidades. Aquí, la masa y la aceleración bastan, como muestra la tabla de dimensiones reescrita: Usando la notación [a] para “las dimensiones de a”, las dimensiones de W son M x [a] y las dimensiones de g son solo [a].

W	M x [a]	peso
m	M	masa
g	[a]	gravedad

En resumen, las tres cantidades contienen sólo dos dimensiones independientes. Tres cantidades menos dos dimensiones independientes producen un grupo adimensional independiente. En consecuencia, el atajo de conteo revisado es

número de cantidades

- número de dimensiones independientes

_____________________________________

número de grupos adimensionales independientes

Este atajo, conocido como el teorema de Buckingham Pi [4], lleva el nombre de Edgar Buckingham y su notación Pi (π) mayúscula para grupos adimensionales. (También es el teorema rank-nulidad del álgebra lineal [42].)

Ejercicio\(\PageIndex{1}\): Bounding the number of independent dimensionelss groups

¿Por qué el número de grupos adimensionales independientes nunca es mayor que el número de cantidades?

Ejercicio\(\PageIndex{2}\): Counting dimensionless groups

¿Cuántos grupos adimensionales independientes producen los siguientes conjuntos de cantidades?

a. periodo T de un sistema resorte-masa en un campo gravitacional: T, k (constante de resorte), m, x ₀ (amplitud) y g.

b. velocidad de impacto v de un objeto de caída libre: v, g y h (altura inicial de caída).

c. velocidad de impacto v de un objeto de caída libre lanzado hacia abajo: v, g, h y v ₀ (velocidad de lanzamiento).

Ejercicio\(\PageIndex{3}\): Using angular frequency instead of speed

Rehacer la derivación de análisis dimensional de la aceleración circular utilizando el radio r y la frecuencia angular\(\omega\) como variables independientes. Usando a = v ²/r, encuentra la constante adimensional en la forma adimensional general

\[\textrm{dimensionless group proportional to } a= \textrm{dimensionless constant}\]

Ejercicio\(\PageIndex{4}\): Impact speed of a dropped object

Utilice el análisis dimensional para estimar la velocidad de impacto de una roca que cae libremente que cae desde una altura

Ejercicio\(\PageIndex{5}\): Speed of gravity waves on deep water

En este problema, se utiliza el análisis dimensional para encontrar la velocidad de las olas en océano abierto. Estas olas son las que verías desde un avión y son impulsadas por la gravedad. Su velocidad podría depender de la gravedad g, su frecuencia\(\omega\) angular y la densidad del agua\(\rho\). Haga el análisis de la siguiente manera.

v	LT ^-1	velocidad de onda
g	LT ^-2	gravedad
\(\omega\)	T ^-1	angular freq.
\(rho\)	ML ^-3	densidad de agua

a. Explique por qué estas cantidades producen un grupo adimensional independiente.

b. ¿Cuál es el grupo proporcional a v?

c. Con la información adicional de que la constante adimensional es 1, predice la velocidad de las olas con un periodo de 17 segundos (puedes medir el periodo cronometrando el intervalo entre la llegada de cada ola a la orilla). Esta velocidad es también la velocidad de los vientos que produjeron las olas. ¿Es una velocidad razonable del viento?

d. ¿Cuál sería la constante adimensional si, en la tabla de cantidades,\(\omega\) se sustituyera la frecuencia angular por el periodo T?

Ejercicio\(\PageIndex{6}\): Using period instead of speed

Al encontrar una fórmula para la aceleración circular (Sección 5.1.1), nuestras variables independientes fueron el radio r y la velocidad v. Rehacer la derivación de análisis dimensional utilizando el radio r y el periodo T como variables independientes.

a. Explique por qué todavía hay un solo grupo adimensional independiente.

b. ¿Cuál es el grupo adimensional independiente proporcional a a a?

c. ¿A qué constante adimensional es igual este grupo?