5.2: Un grupo adimensional

El uso más frecuente del análisis dimensional involucra un grupo adimensional independiente, por ejemplo, ar/v ² en nuestro análisis de aceleración circular (Sección 5.1.1). Veamos más de cerca este tipo de casos, que tiene lecciones para problemas más complicados.

5.2.1 Constantes universales

Lo que encontraremos es que el análisis dimensional reduce la complejidad al generar resultados con amplia aplicación. Es decir, en la forma general

\[\textrm{independent dimensionless group} = \textrm{dimensionless constant,}\]

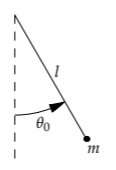
la constante adimensional es universal. Veamos qué significa universal a través de un ejemplo: el análisis de un péndulo de pequeña amplitud. Entonces, imagina soltar un péndulo desde un ángulo pequeño\(\theta_{0}\).

¿Cuál es su periodo de oscilación?

El primer paso en el análisis dimensional es enumerar las cantidades relevantes. La lista comienza con la cantidad objetivo, aquí, el periodo T. Depende de la gravedad g, la longitud de la cuerda l, tal vez la masa m del bob, y tal vez la amplitud\(\theta_{0}\). Afortunadamente, cuando la amplitud es pequeña, como es aquí, entonces la amplitud resulta que no importa, así que no la enumeraremos.

T	T	periodo
g	LT ^-2	gravedad
l	L	longitud de cadena
m	M	masa de bob

¿Cuáles son los grupos adimensionales?

Estas cuatro cantidades contienen tres dimensiones independientes (M, L y T). Por el teorema de Buckingham Pi (Sección 5.1.2), producen un grupo adimensional independiente. Este grupo no puede contener m, porque m es la única cantidad con dimensiones de masa. Un grupo adimensional simple es gT ^2/l. Sin embargo, debido a que nuestro objetivo final es el periodo T, hagamos un grupo adimensional proporcional a la T misma en lugar de a T ². Este grupo lo es\(T \sqrt{g/l}\). Entonces la declaración adimensional más general es

\[T\sqrt{\frac{g}{l}}=C,\]

donde C es una constante adimensional. A pesar de que su valor es, por el momento, desconocido, es universal. La misma constante se aplica a un péndulo con una cuerda más corta o, quizás más sorprendentemente, a un péndulo en Marte, con su diferente fuerza gravitacional. Si encontramos la constante para un péndulo en un planeta, la conocemos para todos los péndulos en todos los planetas.

Hay al menos tres formas de encontrar C. El primero es resolver la ecuación diferencial del péndulo, que es un trabajo duro. El segundo enfoque es resolver un problema más simple inteligentemente diseñado (Problema 3.4). Aunque el enfoque es inteligente, no es tan general como el tercer método.

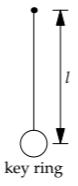
¡El tercer método es medir C con un experimento casero! Para ello, convertí mi llavero en un péndulo colgándolo de una cuerda. La cuerda era aproximadamente el doble de la longitud del papel carta estadounidense (así, 2 × 11 pulgadas) y el período fue de aproximadamente 1.5 segundos. Por lo tanto,

\[C=T\sqrt{\frac{g}{l}} \approx 1.5s \times \sqrt{\frac{32 ft s^{-2}}{2ft}} = 6.\]

¿La constante sería diferente en un moderno sistema de unidades?

En unidades métricas, g ≈ 9.8 metros por segundo por segundo, l ≈ 0.6 metros, y C es, dentro de las inexactitudes de cálculo, todavía 6:

\[C \approx 1.5s \times \sqrt{\frac{9.8m/s^{2}}{0.6m}} \approx 6\]

El sistema de unidades no importa, que es la razón para usar grupos adimensionales: Son invariantes bajo un cambio de unidades. Aun así, probablemente no aparecería un 6 explícito si resolviéramos honestamente la ecuación diferencial del péndulo. Pero una medición más precisa de C podría sugerir una forma cerrada para esta constante adimensional.

La longitud del péndulo, desde el nudo donde lo sostengo hasta el centro del llavero es de 0.65 metros (ligeramente más larga que la estimación aproximada de 0.6 metros). En tanto, 10 periodos tardaron 15.97 segundos. Entonces C está cerca de 6.20:

\[C \approx 1.597 s \times \sqrt{\frac{9.8 m s^{-2}}{0.65m}} \approx 6.20.\]

¿Qué números adimensionales podrían producir 6.20?

Este valor es cercano a 2π, que es aproximadamente 6.28. Esa conjetura se siente como un salto, pero ten coraje. La suposición es plausible una vez que recordamos que los péndulos oscilan y las oscilaciones a menudo involucran 2π, o que estamos pidiendo el período más que la frecuencia angular, una elección que a menudo introduce un 2π (como en el Problema 5.11 (d)). El periodo resultante T es

\[T = C \sqrt{\frac{l}{g}} = 2 \pi \sqrt{\frac{l}{g}}.\]

(Para una explicación física del 2π, intente Problema 3.4.)

Este ejemplo muestra cómo el análisis dimensional, un enfoque matemático, se asienta entre dos enfoques físicos. Primero utilizamos nuestro conocimiento físico para enumerar las cantidades relevantes. Luego redujimos el espacio de posibles relaciones mediante el uso del análisis dimensional. Por último, para encontrar la constante universal C, que el análisis dimensional no podía decirnos, volvimos a utilizar el conocimiento físico (un experimento hogareño).

Ejercicio\(\PageIndex{1}\): Your own measurement

Haz tu propio péndulo y mide la constante universal\(T \sqrt{g/l}.\)

Ejercicio\(\PageIndex{2}\): Period of a spring-mass system

Utilice el análisis dimensional para encontrar, a excepción de una constante adimensional, el periodo T de un sistema resorte-masa con constante de resorte k, masa m y amplitud x ₀. Encuentra la constante adimensional en la declaración adimensional más general

\(\textrm{group proportional to} T = \textrm{dimensionless constant}\)

Ejercicio\(\PageIndex{3}\): Speed of waves in shallow water

En aguas poco profundas, donde la longitud de onda es mucho mayor que la profundidad, las olas impulsadas por la gravedad viajan a una velocidad que podría depender de la gravedad g, la profundidad del agua h y la densidad del agua\(\rho\).

a. encontrar el grupo adimensional independiente proporcional a v ², donde v es la velocidad de ola. Comparar este grupo con el número de Froude, la relación adimensional que introdujimos para estudiar la marcha (Sección 5.1.1).

b. ¿Cuál es entonces el exponente de escalado\(\beta\) en la relación de escalado\(v \: \propto \: h^{\beta}\)? Pon a prueba tu predicción midiendo v (1cm) y v (4cm). Para hacer la medición, llene una fuente para hornear con agua y excita una ola ondulada levantando ligeramente y fijando rápidamente un extremo del plato.

c. Usando sus datos, estime la constante universal (adimensional) en la relación

\[\textrm{dimensionless group from part (a)} = \textrm{dimensionless constant.}\]

d. Predecir la velocidad de las mareas, que son (¡aguas poco superficiales!) olas creadas por sismos submarinos. ¿Cuánto tarda un maremoto en cruzar un océano?

5.2.2 Energía de explosión atómica

Los problemas con un solo grupo adimensional no necesitan ser simples o fáciles de usar por otros métodos. Un ejemplo clásico es encontrar la energía liberada por la primera bomba atómica, detonada en el desierto de Nuevo México en 1945. La energía explosiva, o rendimiento, era de alto secreto. Sin embargo, fotografías desclasificadas de la explosión, debido a que tenían una barra de escala, proporcionaban datos sobre el radio de la bola de fuego en varias ocasiones después de la explosión. Los datos deben haber parecido lo suficientemente inocuos como para liberarlos.

t (ms)	R (m)
3.26	59.0
4.61	67.3
15.0	106.5
62.0	185.0

Pero a partir de estos datos, G. I. Taylor de la Universidad de Cambridge predijo el rendimiento [44]. El análisis, como muchos cálculos en mecánica de fluidos, es largo y complicado. En su lugar, usaremos el análisis dimensional para encontrar la relación entre el radio de voladura R, el tiempo t desde la explosión, la energía E de explosión y la densidad del aire\(\rho\). Luego usaremos los datos R (t) para predecir E.

Estas cuatro cantidades contienen tres dimensiones independientes. Así, producen un grupo adimensional independiente. Para encontrarlo, eliminemos una dimensión a la vez. Aquí, un poco de suerte simplifica el proceso, porque tenemos dimensiones que son fáciles de eliminar.

E	ML ^2 T ^-2	energía de explosión
R	L	radio de explosión
t	T	tiempo desde explosión
\(rho_{air}\)	ML ^-3	densidad del aire

¿Ocurre alguna dimensión en solo una o dos cantidades?

Sí: La masa ocurre en E como M ¹ y en\(\rho_{air}\) también como M ¹; el tiempo aparece en E como T ⁻² y en t como T ¹. Por lo tanto, para eliminar la masa, el grupo adimensional debe contener E/\(\rho_{air}\). Para eliminar el tiempo, el grupo adimensional debe contener Et ². Así, Et ²/\(\rho_{air}\)elimina la masa y el tiempo. Debido a que tiene dimensiones de L ⁵, la única manera de eliminar estas dimensiones sin introducir ninguna potencia de tiempo o masa es dividiendo por R ⁵. El resultado, Et ²/\(\rho_{air}R^{5}\), es un grupo adimensional independiente. También es el único grupo adimensional proporcional a nuestro objetivo, la energía explosiva E.

Con un solo grupo adimensional, la declaración adimensional más general sobre la energía de voladura es

\[\frac{Et^{2}}{\rho_{air}R^{5}} \sim 1\]

Para una explosión particular, E es fijo (aunque desconocido), tal como está\(\rho_{air}\). Por lo tanto, estas cantidades abandonan la relación de escalado correspondiente, que se convierte en\(t^{2} \: \propto \: R^{5}\) o\(R \: \propto \: t^{2/5}\). En los ejes log—log, los datos sobre el radio de voladura deben caer a lo largo de una línea de pendiente 2/5, como lo hacen casi exactamente:

Con el resultado del análisis dimensional\(Et^{2}/\rho_{air}R^{5} \sim 1\), cada punto predice una energía explosiva de acuerdo con\(E \sim \rho_{air}R^{5}/t^{2}/\) Usando 1 kilogramo por metro cúbico para\(\rho_{air}\), las estimaciones de E se encuentran entre 5.6 y 6.7 x 10 ¹³ julios. Desafortunadamente para juzgar la precisión de la estimación, los julios son una unidad poco familiar para la energía de una explosión de bomba. La unidad familiar es toneladas de TNT.

¿Cuál es la energía de explosión predicha como masa de TNT?

Un gramo de TNT libera 1 kilocaloría o aproximadamente 4 kilojulios. Contiene solo una cuarta parte de la densidad energética del azúcar, ¡pero la energía se libera mucho más rápidamente! Un kilotón es de 10 ⁹ gramos, que liberan 4× 10 ¹² julios. Nuestro rendimiento previsto de 6×10 ¹³ julios es, por lo tanto, aproximadamente 15 kilotones de TNT.

Solo por diversión, si reestimamos el rendimiento usando una densidad de aire más precisa de 1.2 kilogramos por metro cúbico, la energía de explosión sería de 18 kilotones. Este resultado es sorprendentemente preciso considerando el número de aproximaciones que contiene: El rendimiento clasificado fue de 20 kilotones. (La constante universal que falta para las explosiones de ondas de choque debe estar muy cerca de 1.)

¡El análisis dimensional es poderoso!