5.6: Resumen y problemas adicionales

Una cantidad con dimensiones no tiene sentido por sí misma. Como podría haberlo dicho Sócrates, no vale la pena conocer la cantidad no comparada. Usando este principio, aprendimos a reescribir relaciones en forma adimensional: en términos de combinaciones de las cantidades donde la combinación no tiene dimensiones. Debido a que el espacio de las relaciones adimensionales es mucho más pequeño que el espacio de todas las relaciones posibles, esta reescritura simplifica muchos problemas. Al igual que las otras dos herramientas de la Parte II, el análisis dimensional descarta la complejidad sin pérdida de información.

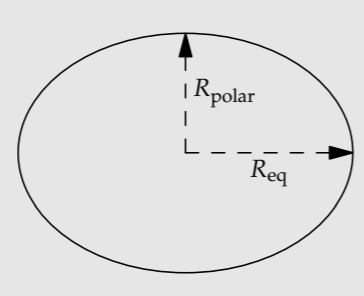
Problema 5.46: Oblatez de la Tierra

Oblatez de la Tierra

Debido a que la Tierra gira sobre su eje, es una esfera oblata. Se puede estimar la oblatitud usando análisis dimensional y algunas adivinanzas. Nuestra medida de oblatitud será\(\Delta R = R_{eq} - R_{polar}\) (la diferencia entre los radios polares y ecuatoriales). Encuentra dos grupos adimensionales independientes construidos a partir de\(\Delta R\), g, R (el radio medio de la Tierra) y\(v\) (la velocidad de rotación de la Tierra en el ecuador). Adivina una relación razonable entre ellos para poder estimar\(\Delta R\). Después compara tu estimación con el valor real, que es aproximadamente de 21.4 kilómetros.

Problema 5.47: Enormes olas en aguas profundas

Una de las olas oceánicas medidas más altas fue encontrada en 1933 por un engrase de la Marina de los Estados Unidos, el USS Ramapo (un barco de 147 metros de largo) [34]. El periodo de ola fue de 14.8 segundos. Encuentra su longitud de onda usando los resultados de Problema 5.11. ¿Una ola de esta longitud de onda sería peligrosa para la nave?

Problema 5.48: Patinaje sobre Hielo

Para el patinaje sobre hielo récord mundial, estime la potencia consumida por la fricción deslizante. (Los patines de hielo que se deslizan sobre hielo tienen un coeficiente de fricción de deslizamiento alrededor de 0.005.) Luego, haz que ese poder sea significativo estimando la relación

\[\frac{\textrm{power consumed in sliding friction}}{\textrm{power consumed by air resistance}}.\]

Problema 5.49: Fusión por presión durante el patinaje sobre hielo

El agua se expande cuando se congela. Así, aumentar la presión sobre el hielo debería, por principio de Le Chatelier, empujarlo a convertirse en agua, lo que disminuye su punto de congelación. Con base en el punto de congelación y el calor de vaporización del agua, estimar el cambio en el punto de congelación causado por cuchillas de patines de hielo. ¿Este cambio es lo suficientemente grande como para explicar por qué las cuchillas de patines de hielo se deslizan con muy poca fricción sobre una fina lámina de agua

Problema 5.50: Radio de contacto

Una bola sólida de radio R\(\rho\), densidad y módulo elástico Y descansa sobre el suelo. Usando el análisis dimensional, ¿cuánto se puede deducir sobre el radio de contacto r?

Problema 5.51: Tiempo de contacto

El balón de Problema 5.50 se cae desde una altura, golpea una mesa dura con velocidad\(v\), y rebota. Usando el análisis dimensional, ¿cuánto se puede deducir sobre el tiempo de contacto?

Problema 5.52: Flotando en el agua

Algunos insectos pueden flotar en el agua gracias a la tensión superficial del agua. En términos del tamaño de error l (una longitud), encuentre los exponentes de escalado\(\alpha\) y\(\beta\) en

\[F_{\gamma} \: \propto \: l^{\alpha}, \]

\[W \: \propto \: l^{\beta},\]

donde\ (F_ {\ gamma}\] es la fuerza de tensión superficial y W es el peso del insecto. (La tensión superficial en sí tiene dimensiones de fuerza por longitud). Con ello explicar por qué un insecto lo suficientemente pequeño puede flotar en el agua.

Problema 5.53: Medidas adimensionales de amortiguación

Un sistema amortiguado de muelle-masa tiene tres parámetros: la constante elástica k, la masa m y la constante de amortiguación\(\gamma\). La constante de amortiguación determina la fuerza de amortiguación a través\(F \gamma = \gamma v\), donde\(v\) está la velocidad de la masa.

a. Utilice estas cantidades para hacer que el grupo adimensional sea proporcional a\(\gamma\). Los ingenieros mecánicos y estructurales utilizan este grupo para definir la relación de amortiguación adimensional\(\zeta\):

\[\zeta \equiv \frac{1}{2} \times \textrm{ the dimensionless group proportional to } \gamma.\]

b. Encontrar el grupo adimensional proporcional a\(\gamma^{-1}\). Físicos e ingenieros eléctricos, siguiendo convenciones desde los primeros días de la radio, llaman a este grupo el factor de calidad Q.

Problema 5.54: Cable de acero bajo su propio peso

¡La rigidez de un material no debe confundirse con su resistencia! La fuerza es la tensión (una presión) a la que se rompe la sustancia; se denota\(\sigma_{y}\). Al igual que la rigidez, es una densidad de energía. La relación adimensional\(\sigma_{y}/\sigma\), llamada deformación de rendimiento\(\epsilon_{y}\), tiene una interpretación física: el cambio de longitud fraccional en el que se rompe la sustancia. Para la mayoría de los materiales, se encuentra en el rango de 10 ⁻³... 10 ⁻² —con materiales quebradizos (como la roca) hacia el extremo inferior. Usando la información anterior, estime la longitud máxima de un cable de acero antes de que se rompa bajo su propio peso.

Problema 5.55: Dinámica orbital

Un planeta orbita al Sol en una elipse que se puede describir por la distancia de aproximación más cercana r _min y por la distancia más alejada r _max. La longitud l es su media armónica:

\[l = 2 \frac{r_{min}r_{max}}{r_{min}+r_{max}} = 2(r_{min} \parallel r_{max}).\]

(Volverás a encontrar la media armónica en Problema 8.22, como ejemplo de un tipo de media más general).

La tabla da r _min y r _max para los planetas, así como el potencial efectivo específico V, que es la energía potencial efectiva dividida por la masa planetaria m (el potencial efectivo en sí mismo mezcla el potencial gravitacional energía con un componente de la energía cinética). El propósito de este problema es ver cómo las funciones universales organizan este conjunto de datos aparentemente desordenado.

	r min (m)	r máx (m)	V (m ^2 s ^-2)
Mercurio	4.6001 x 10 ^10	6.9818 x 10 ^10	-1.1462 x 10 ^9
Venus	1.0748 x 10 ^11	1.0894 x 10 ^11	-6.1339 x 10 ^8
Tierra	1.4710 x 10 ^11	1.5210 x 10 ^11	-4.4369 x 10 ^8
Marte	2.0666 x 10 ^11	2.4923 x 10 ^11	-2.9199 x 10 ^8
Júpiter	7.4067 x 10 ^11	8.1601 x 10 ^11	-8.5277 x 10 ^7
Saturno	1.3498 x 10 ^12	1.5036 x 10 ^12	-4.6523 x 10 ^7
Urano	2.7350 x 10 ^12	3.0063 x 10 ^12	-2.3122 x 10 ^7
Neptuno	4.4598 x 10 ^12	4.5370 x 10 ^12	-1.4755 x 10 ^7

a. en una gráfica de V versus r, graficar todos los datos. Cada planeta proporciona dos puntos de datos, uno para r = r _min y otro para r=r _máx. La trama debe ser un desastre. Pero lo enderezarás en el resto del problema.

b. Ahora escribe la relación entre V y r en forma adimensional. Las cantidades relevantes son v, r, GM _Sun, y la longitud l. Elige tus grupos para que V aparezca solo en un grupo y r aparezca solo en un grupo separado.

c. Ahora use la forma adimensional para volver a trazar los datos en forma adimensional. Todos los puntos deben estar en una curva. Usted ha encontrado la función universal que caracteriza todas las órbitas planetarias

Problema 5.56: Velocidad de propagación de señal en cable coaxial

Para el cable coaxial del Problema 2.25, estime la velocidad de propagación de la señal.

Problema 5.57: Barra de medidor bajo presión

Estimar cuánto más corta se vuelve una barra de medidor de acero debido a que se coloca en el fondo del océano. ¿Y un bastón medidor hecho de madera?

Problema 5.58: Velocidad del sonido en el agua

Utilizando el calor de vaporización del agua como medida de la densidad de energía en sus enlaces más débiles, estimar la velocidad del sonido en el agua.

Problema 5.59: Potencial de función Delta

Un potencial simple utilizado como modelo para entender moléculas es el potencial de función delta unidimensional\(V(x) = -E_{0}L\delta(x)\), donde E ₀ es una energía y L es una longitud (imagínese un potencial profundo de profundidad E ₀ y ancho pequeño L). Utilice el análisis dimensional para estimar la energía del estado fundamental.

Problema 5.60: Flujo de tubo

En este problema se estudia el flujo de fluido a través de un tubo estrecho. La cantidad a predecir es Q, el caudal volumétrico (volumen por tiempo). Esta tasa depende de cinco cantidades:

l	la longitud del tubo
\(\Delta p\)	la diferencia de presión entre los extremos del tubo
r	el radio del tubo
\(\rho\)	la densidad del fluido
\(\nu\)	la viscosidad cinemática del fluido

a. Encuentre tres grupos adimensionales independientes G ₁, G ₂ y G ₃ a partir de estas seis cantidades, preparándose para escribir la declaración más general como

\[\textrm{group 1} = f(\textrm{group 2, group 3}).\]

Pista: Un grupo físicamente razonable es\(G_{2} = r/l\); para hacer posible la resolución de Q, poner Q solo en el grupo 1 y hacer que este grupo sea proporcional a Q.

b. ahora imagina que el tubo es largo y delgado (l >> r) y que el radio o velocidad de flujo es lo suficientemente pequeño como para hacer que el número de Reynolds sea bajo. Luego deducir la forma de f usando razonamiento proporcional: Primero encuentre el exponente de escalado\(\beta\) en\(Q \: \alpha \: (\Delta p)\beta\); luego encuentre el exponente de escalado\(\gamma\) en\(Q \: \alpha \: l \gamma\). Pista: Si doblas\(\Delta p\) y l, ¿qué debería pasar con Q?

Determinar la forma de f que satisfaga todos sus requisitos de proporcionalidad. Si te quedas atascado, trabaja hacia atrás desde el resultado correcto. Busque el flujo de Poiseuille, y use el resultado para deducir las proporcionalidades precedentes; y luego dar razones de por qué son así

c. El análisis en las partes anteriores no le da la constante universal, adimensional. Use una jeringa y aguja para estimar la constante. Compara tu estimación con el valor que viene de resolver honestamente las ecuaciones de la mecánica de fluidos (buscando este valor).

Problema 5.61: Hervido versus ebullición

Busque el calor específico del agua en la tabla de constantes (p. xvii) y estime la relación

\[\frac{\textrm{energy to bring a pot of water to boiling temperature}}{\textrm{energy to boil away the boiling water}}.\]

Problema 5.62: Ley de Kepler para órbitas elípticas

La tercera ley de Kepler conecta el período orbital con los radios orbitales mínimo y máximo r _min y r _max y con la fuerza gravitacional del Sol:

\[T = 2 \pi \frac{a^{3/2}}{\sqrt{GM_{Sun}}},\]

donde el eje semimajor a se define como\(a \equiv (r_{min}+r_{max})/2\). Escribe la tercera ley de Kepler en forma adimensional, haciendo un grupo adimensional independiente proporcional a T y el otro grupo proporcional a r _min.

Problema 5.63: ¿Por qué Marte?

¿Por qué Kepler necesitaba datos sobre la órbita de Marte para concluir que los planetas orbitaban el Sol en una elipse en lugar de un círculo? Pista: Ver los datos en Problema 5.55.

Problema 5.64: Número de Froude para la velocidad del casco de un barco

Para un barco, la velocidad del casco se define como

\[v = \equiv 1.34 \sqrt{l},\]

donde\(v\) se mide en nudos (millas náuticas por hora), y l, la longitud de la línea de flotación, se mide en pies. La longitud de la línea de flotación es, como cabría esperar, la longitud de la embarcación medida en la línea de flotación. La velocidad del casco es la velocidad máxima de un barco antes de que el arrastre de agua se vuelva muy grande.

Convertir esta fórmula específica de la unidad a un número Froude aproximado Fr, el número adimensional introducido en la Sección 5.1.1 para estimar la velocidad máxima de marcha. Para la velocidad del casco, el número de Froude se define como

\[\textbf{Fr} \equiv \frac{v^{2}}{gl}.\]

Del número aproximado de Froude, ¡adivina el valor exacto!