1.4: Un modelo de sistema electromecánico

Modelo de un motor de CC

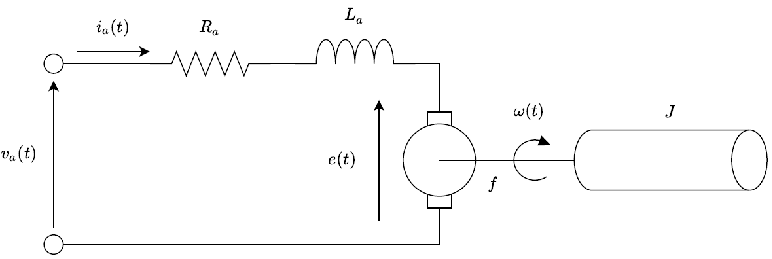
Un sistema electromecánico convierte la energía eléctrica en energía mecánica o viceversa. Un motor de CC controlado por armadura (Figura 1.4.1) representa dicho sistema, donde la entrada es el voltaje de la armadura\(V_{ a} (t)\), y la salida es la velocidad del motor\(\omega (t)\), o posición angular\(\theta (t)\).

Para desarrollar un modelo del motor de CC, vamos a\(i_{ a} (t)\) denotar la corriente del inducido,\(L\) y\(R\) denotar la inductancia lateral eléctrica y la resistencia de la bobina. La inercia lateral mecánica y la fricción se denotan como\(J\) y\(b\), respectivamente. Dejar\(k_{ t}\) denotar la constante de par y\(k_{b}\) la constante del motor; entonces, las ecuaciones dinámicas del motor de CC se dan como:

\[L\frac{ d i_{a} (t)}{ d t} +Ri_{a} (t)+k_{ b} \omega (t)=V_{ a} (t)\]

\[J\frac{ d \omega (t)}{ d t} +b\omega (t)-k_{ t} i_{ a} (t)=0\]

Mediante el uso de la transformada de Laplace, estas ecuaciones se transforman en ecuaciones algebraicas como:

\[(Ls+R)i_{ a} (s)+k_{ b} \omega (s)=V_{ a} (s)\]

\[(Js+b)\omega (s)-k_{ t} i_{ a} (s)=0\]

Figura\(\PageIndex{1}\): Esquema de un motor de CC controlado por armadura.

Función de transferencia del motor

Para obtener una relación entrada-salida para el motor de CC, podemos resolver la primera ecuación\(i_a(s)\) y sustituirla en la segunda ecuación. Alternativamente, multiplicamos la primera ecuación por\(k_{ t}\), la segunda ecuación por\((Ls+R)\), y las sumamos para obtener:

\[(Ls+R)(Js+b)\omega (s)+k_{ t} k_{ b} \omega (s)=k_{ t} V_{ a} (s)\]

Luego, la función de transferencia del motor de CC con entrada de voltaje y salida de velocidad angular se deriva como:

\[\frac{\omega (s)}{V_{ a} (s)} =\frac{k_{ t} }{(Ls+R)(Js+b)+k_{ t} k_{ b} }\]

El polinomio denominador en la función de transferencia del motor de CC generalmente tiene raíces reales, que son recíprocas de las constantes de tiempo motoras\((\tau _{ e} ,\; \tau _ m )\). En términos de las constantes de tiempo, el modelo de motor de CC se describe como:

\[\frac{\omega (s)}{V_{ a} (s)} =\frac{k_{ t} /JL}{(s+1/\tau _{ e} )(s+1/\tau _ m )}\]

La constante eléctrica representa la acumulación de corriente eléctrica en el circuito de la armadura, donde la constante mecánica representa la acumulación de velocidad del motor en respuesta al par motor desarrollado. Además, la constante de tiempo mecánica más lenta domina la respuesta general del motor a un cambio en el voltaje de la armadura.

La posición angular\(\theta \left(s\right)\) del eje se obtiene integrando la velocidad angular\(\omega (s)\); la función de transferencia desde\(V_a(s)\) el desplazamiento angular\(\theta \left(s\right)\) se da como:

\[\frac{\theta (s)}{V_{ a} (s)} =\frac{k_{ t} }{s\left[(Ls+R)(Js+b)+k_{ t} k_{ b} \right]}\]

Ejemplo\(\PageIndex{1}\)

Un pequeño motor de CC tiene los siguientes valores de parámetros:\(R=1\Omega ,\; L=0.01H,\; J=0.01\; kgm^{2} ,\; b=0.1\; \frac{N-s}{rad} ,\; and\; k_{t} =k_{b} =0.05\); entonces, la función de transferencia del motor desde el voltaje de la armadura hasta la velocidad angular se obtiene como:

\[\frac{\omega (s)}{V_{ a} (s)} =\frac{500}{(s+100)(s+10)+25} =\frac{500}{(s+10.28)(s+99.72)}\]

Las dos constantes de tiempo del motor se dan como:\(\tau _{ e} \cong 1\; 0 ms,\; \tau _ m \cong 100\; ms\), donde\({\tau }_e\) coincide la constante de tiempo de un circuito RL (\({\tau }_e=L/R\)) y\({\tau }_m\) coincide con la constante de tiempo de la masa inercial en presencia de fricción (\({\tau }_m=J/b\)).

Suponiendo que una entrada unidad-paso\(u(s)=\frac{1}{s}\),, se aplica al motor, la velocidad del motor se obtiene como:

\[\omega \left(s\right)=\frac{500}{s\left(s+10.28\right)\left(s+99.72\right)}=\frac{0.488}{s}-\frac{0.544}{s+10.28}+\frac{0.056}{s+99.72}\]

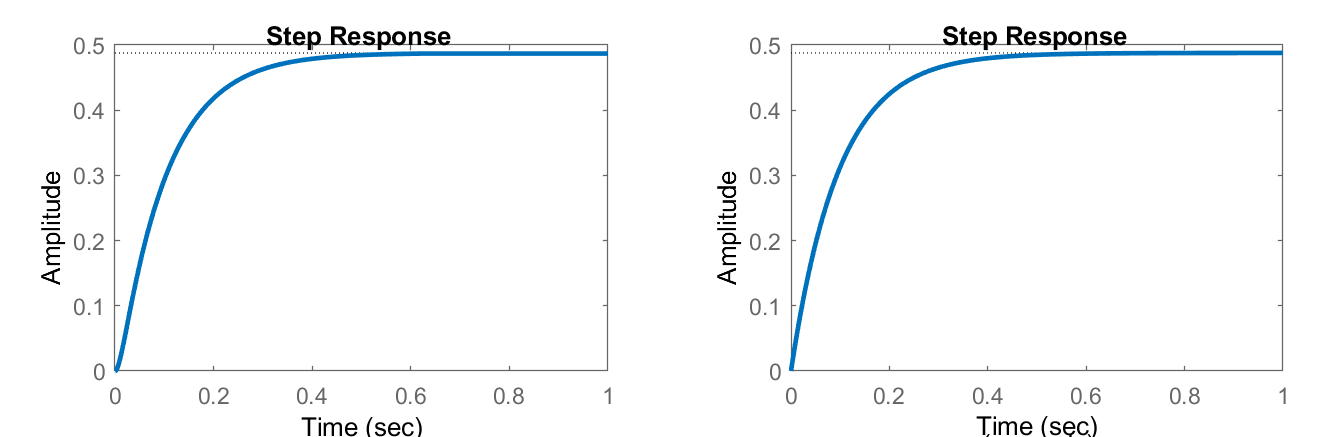
Al aplicar la transformada inversa de Laplace, la salida en el dominio del tiempo se da como (Figura 13a):

\[\omega \left(t\right)=\left[0.488-0.544e^{-10.28t}+0.056e^{-99.72t}\right]u\left(t\right)\]

donde\(u\left(t\right)\) denota una función unidad-paso. La respuesta motora se representa en la Figura 1.4.2.

Modelo simplificado de un motor de CC

Se obtiene un modelo simplificado del motor de CC ignorando la inductancia de la bobina (\(L\to 0\)). Luego, la ecuación del lado eléctrico se modifica como:

\[Ri_a\left(s\right)+k_b\omega \left(s\right)=V_a(s)\]

Al sustituir\(i_a\left(s\right)\) en la ecuación de par, la ecuación del lado mecánico se da como:

\[R(Js+b)\omega (s)+k_{ t} k_{ b} \omega (s)=k_{ t} V_{ a} (s)\]

La función de transferencia de motor de primer orden resultante se da como:

\[\frac{\omega (s)}{V_{ a} (s)} =\frac{k_{ t} /R}{Js+b+k_{ t} k_{ b} /R}\]

El modelo de primer orden tiene una sola constante de tiempo del motor\(\left(\tau _ m =\frac{JR}{bR+k_{ t} k_{ b} } \right)\), y está escrito como:

\[\frac{\omega (s)}{V_{ a} (s)} =\frac{k_{ t} /JR}{s+1/\tau _m }\]

Ejemplo\(\PageIndex{2}\)

Usando los valores de los parámetros para un motor de CC pequeño (Ejemplo 1.4.1), su función de transferencia de primer orden reducida se obtiene como:

\[\frac{\omega (s)}{V_{ a} (s)} =\frac{5}{s+10.25}\]

La constante de tiempo del motor resultante se evalúa como:\(\tau _{m} \cong 97.6\; ms\), que se aproxima a la constante de tiempo mecánica más lenta en el modelo de segundo orden.

Suponiendo una entrada unidad-paso, la respuesta del motor se obtiene como:

\[\omega \left(s\right)=\frac{5}{s\left(s+10.25\right)}=\frac{0.488}{s}-\frac{0.488}{s+10.25}\]

Al aplicar la transformada inversa de Laplace, la salida del motor se da como:

\[\omega \left(t\right)=\left[0.488-0.488e^{-10.25t}\right]u\left(t\right)\]

La respuesta del motor a una entrada unidad-paso se representa en la Figura 1.4.2.

Figura\(\PageIndex{2}\): Respuesta del motor de CC a la entrada unidad-paso: modelo de motor de segundo orden (izquierda); modelo de motor de primer orden (derecha).

pkg load control
R=1; L=.01; J=.01; b=.1; kt=.05; kb=.05;
s=tf('s');
Gs=kt/((L*s+R)*(J*s+b)+kt*kb)
step(Gs), hold
L=0;
Gs1=kt/((L*s+R)*(J*s+b)+kt*kb)
step(Gs1)