1.3: Modelos ODE de segundo orden

Modelos ODE de segundo orden

Un sistema físico que contiene dos elementos de almacenamiento de energía es descrito por una ODE de segundo orden. Ejemplos de modelos de segundo orden se discuten a continuación:

Ejemplo\(\PageIndex{1}\)

Un circuito RLC en serie con entrada de voltaje\(V_s(t)\) y salida de corriente\(i(t)\) tiene una relación de gobierno obtenida aplicando la ley de voltaje de Kirchoff a la malla (Figura 1.3.1):

\[L\frac{ di(t)}{ dt} +Ri(t)+\frac{1}{C} \int i(t) dt=V_ s (t)\]

La ecuación integrodiferencial anterior puede convertirse en una ODE de segundo orden expresándola en términos de la carga eléctrica\(q(t)\), como:

\[L\frac{ d^{2} q(t)}{ dt^{2} } +R\frac{ dq(t)}{ dt} +\frac{1}{C} q(t)=V_ s (t)\]

Alternativamente, el circuito RLC en serie se puede describir en términos de dos ODE de primer orden que involucran variables naturales\(i(t)\), la corriente y la tensión del condensador\(V_c(t)\), como:

\[L\frac{ di(t)}{ dt} +Ri(t)+V_{c} (t)=V_s (t), \ \ \ \ \ C\frac{dV_c}{dt}=i(t)\]

Figura\(\PageIndex{1}\): Un circuito RLC en serie accionado por una fuente de voltaje constante.

Ejemplo\(\PageIndex{2}\)

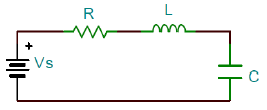
El movimiento de un elemento de masa de peso\(mg\), tirado hacia arriba por una fuerza,\(f(t)\), se describe usando salida de posición,\(y(t)\), por una ODE de segundo orden:

\[m\frac{ d^{2} y(t)}{ dt^{2} } +mg=f(t)\]

La ODE de segundo orden expresa el hecho de que la masa móvil tiene tanto la energía cinética como la potencial (Figura 1.3.2).

Figura\(\PageIndex{2}\): Movimiento de una masa inercial bajo campo gravitacional.

Ejemplo\(\PageIndex{3}\)

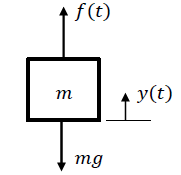
Un sistema de masa-resorte-amortiguador incluye una masa afectada por una fuerza aplicada\(f(t)\); su movimiento es frenado por una combinación de un resorte y un amortiguador (Figura 1.8).

Vamos a\(x(t)\) denotar el desplazamiento de la masa desde una referencia fija; entonces, la ecuación dinámica del sistema, obtenida usando la segunda ley de movimiento de Newton, toma una forma familiar:

\[m\frac{ d^{2} x(t)}{ dt^{2} } +b\frac{ dx(t)}{ dt} +kx(t)=f(t)\]

En notación compacta, podemos expresar la ODE como:\[m\ddot{x}\; +\; b\dot{x}\; +\; kx=f\]

donde los puntos por encima de la variable representan derivada de tiempo, es decir,\(\dot{x}\left(t\right)=\frac{dx\left(t\right)}{dt}\),\(\ddot{x}\left(t\right)=\frac{d^2x\left(t\right)}{dt^2}\).

Usando la posición\(x(t)\), y la velocidad,\(v(t)\) como variables, el sistema masa-resorte-amortiguador se describe mediante dos ecuaciones de primer orden (llamadas ecuaciones de estado) dadas como:\[ \frac{dx}{dt}=v(t), \ \ \ \ \ \frac{dv}{dt}=\frac{1}{m} \left(-kx(t)-bv(t)+f(t) \right)\]

En ausencia de amortiguación, la ecuación dinámica del sistema masa-resorte se reduce a:

\[m\frac{d^2x\left(t\right)}{dt^2}+kx\left(t\right)=f(t)\]

La ecuación anterior describe el movimiento armónico simple (SHM) con\({\omega }^2_0=k/m\). A partir de la física elemental, la solución general a la ecuación se da como:

\[x\left(t\right)=A{cos {\omega }_0\ }t+B{sin {\omega }_0t\ }\]

Figura\(\PageIndex{3}\): Un modelo de sistema masa-resorte-amortiguador.

Resolución de modelos de segundo orden

Un modelo ODE de segundo orden se puede resolver aplicando la transformada de Laplace a ambos lados de la ecuación diferencial. Permita que un modelo general de ODE de segundo orden se describa como:

\[\ddot{y}\left(t\right)+a_1\dot{y}\left(t\right)+a_2y\left(t\right)=b_1\dot{u}\left(t\right)+b_2u\left(t\right)\]

Aplicación de la transformada de Laplace, asumiendo las siguientes condiciones iniciales:\(y\left(0\right)=y_0,\ \ \dot{y}\left(0\right)={\dot{y}}_0, \ \ u(0)=0\), da:

\[\left(s^2+a_1s+a_2\right)y\left(s\right)-\left(s+a_1\right)y_0-{\dot{y}}_0=\left(b_1s+b_2\right)u\left(s\right)\]

o,

\[y\left(s\right)=\frac{1}{s^2+a_1s+a_2}\left[\left(s+a_1\right)y_0+{\dot{y}}_0+\left(b_1s+b_2\right)u\left(s\right)\right]\]

Función de transferencia

Al aplicar la transformación de Laplace asumiendo que no hay condiciones iniciales, obtenemos:\(\left(s^2+a_1s+a_2\right)y\left(s\right)=(b_1s+b_2)u(s)\); la función de transferencia de entrada-salida resultante se da como:

\[\frac{y\left(s\right)}{u\left(s\right)}=\frac{b_1s+b_2}{s^2+a_1s+a_2}\]

La ecuación característica del modelo se define como:\(s^{2} +a_{1} s+a_{2} =0\).

Para el modelo masa-resorte-amortiguador descrito por:\(m\ddot{x}\; +\; b\dot{x}\; +\; kx=f\) (Ejemplo 1.3.3), la función de transferencia de entrada de fuerza a salida de desplazamiento se da como:

\[\frac{x(s)}{f(s)} =\frac{1}{ms^{2} +bs+k} \]

La función de transferencia de un sistema físico es una fracción propia, es decir, el grado del polinomio denominador es mayor que el grado de polinomio numerador.

Las raíces de su polinomio denominador caracterizan la respuesta del modelo ODE de segundo orden. La respuesta es monótona en el caso de raíces reales, y oscilatoria para raíces complejas.

Ejemplo\(\PageIndex{4}\)

Considere el modelo masa-resorte-amortiguador (Ejemplo 1.3.3), donde se asumen los siguientes valores de parámetros:\(m=1,\ k=2,\ b=3\). Entonces, la ODE de segundo orden se da como:

\[\ddot{x}\left(t\right)+3\dot{x}\left(t\right)+2x\left(t\right)=f\left(t\right)\]

La aplicación de la transformada de Laplace asumiendo cero condiciones iniciales da:\[(s^2+3s+2)y\left(s\right)=f(s)\]

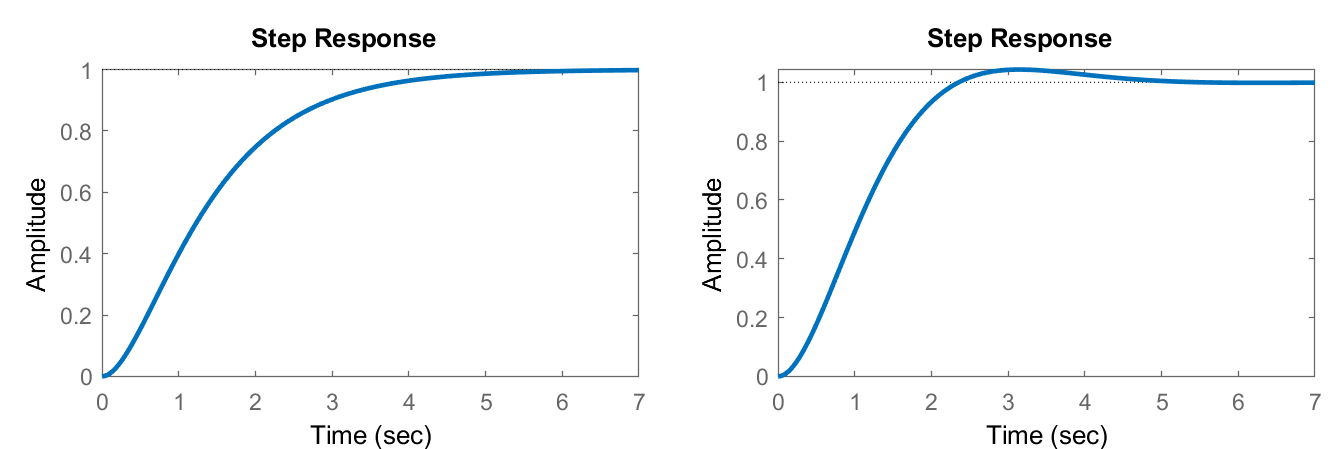
La ecuación característica del modelo se da como:\(s^2+3s+2=0\). La ecuación tiene raíces reales en:\(s=-1,\ -2\).

A continuación, vamos\(f\left(t\right)=2u\left(t\right),\ f\left(s\right)=\frac{2}{s}\); entonces, la salida se resuelve como:\[x\left(s\right)=\frac{2}{s\left(s+1\right)\left(s+2\right)}\]

Utilizamos expansión de fracción parcial (PFE) para obtener:

\[x(s)=\frac{1}{s}-\frac{2}{s+1}+\frac{1}{s+2}\]

Al aplicar la transformada inversa de Laplace, la respuesta de salida del sistema resorte-masa-amortiguador se obtiene como (Figura 1.9):

\[x\left(t\right)=\left(1-2e^{-t}+e^{-2t}\right)u(t)\]

donde\(u\left(t\right)\) representa la función unidad-paso.

Nota: La solución de una ODE generalmente involucra la PFE. Podemos utilizar la calculadora de fracciones parciales Simbolab en línea para este propósito (https://www.symbolab.com/solver/part...ns-calculator/).

Ejemplo\(\PageIndex{5}\)

Considere el modelo masa-resorte-amortiguador (Ejemplo 1.3.3), con los siguientes valores de parámetros:\(m=1,\ k=2,\ b=2\). Entonces, la ODE de segundo orden se da como:

\[\ddot{x}\left(t\right)+2\dot{x}\left(t\right)+2x\left(t\right)=f\left(t\right)\]

La aplicación de la transformada de Laplace asumiendo cero condiciones iniciales da:

\[(s^2+2s+2)y\left(s\right)=f(s)\]

La ecuación característica del modelo se da como:\(s^2+2s+2=0\). La ecuación tiene raíces complejas en:\(s=-1\pm j1\).

Dejar\(f\left(t\right)=2u\left(t\right),\ f\left(s\right)=2/s\); entonces, la salida se resuelve como:

\[x\left(s\right)=\frac{2}{s\left(s^2+2s+2\right)}\]

A continuación, se realiza un PFE de la salida para obtener:

\[x(s)=\frac{1}{s}-\frac{s+2}{s^2+2s+2}\]

El factor cuadrático se expresa como:\({\left(s+1\right)}^2+1^2\); el término cuadrático se divide para obtener:

\[x\left(s\right)=\frac{1}{s}-\frac{s+1}{{\left(s+1\right)}^2+1^2}-\frac{1}{{\left(s+1\right)}^2+1^2}\]

Al aplicar la transformada inversa de Laplace, la respuesta de salida del sistema resorte-masa-amortiguador se obtiene como (Figura 1.9):

\[x\left(t\right)=\left(1-e^{-t}\cos t -e^{-t}\sin t \right)u\left(t\right)\]

donde\(u\left(t\right)\) representa la función unidad-paso.

Figura\(\PageIndex{4}\): Respuesta temporal de modelos de sistema de segundo orden: ecuación característica con raíces reales (izquierda); con raíces complejas (derecha).

pkg load control
s=tf('s');
Gs1=1/(s^2+3*s+2);
Gs2=1/(s^2+2*s+2);
step(Gs1) 
step(Gs2)

Hello world! Hello world!