2.2: Respuesta Natural del Sistema

Respuesta Natural del Sistema

La función de transferencia de un sistema dinámico lineal invariante en el tiempo (LTI) se da como una relación de polinomios:\(G(s)=\frac{n(s)}{d(s)}\). Los polos de la función de transferencia son las raíces del polinomio denominador\(d(s)\).

Los polos de la función de transferencia caracterizan los modos de respuesta natural del sistema. Así, si\(p_i\) es un polo de la función de transferencia\(G\left(s\right)\), entonces\(\left\{e^{p_it}\right\}\) constituye un modo de respuesta natural.

• Un polo real:\(p_i=-\sigma\), aporta un término\(e^{-\sigma t}\) a la respuesta natural del sistema.
• Un par de polos complejos:\(p_i=-\sigma \pm j\omega\), aporta términos oscilatorios de la forma\(e^{-\sigma t}e^{j\omega t}=e^{-\sigma t}\left( \cos \omega t +j \sin \omega t\right)\) a la respuesta natural.

La respuesta natural del sistema es una suma ponderada de los modos de respuesta natural, es decir,\(y_n(t)=\sum_{i=1}^n C_i e^{p_it}\). Además, la respuesta natural se refleja en la respuesta impulsiva de un sistema.

Definición: Respuesta al Impulso

La respuesta de impulso de un sistema, representada por\(G(s)\), se define como la respuesta del sistema a una entrada unidad-impulso\(\delta \left(t\right)\), cuando las condiciones iniciales son cero.

Dejar\(u\left(t\right)=\delta \left(t\right),\ \ u\left(s\right)=1\); entonces, la respuesta al impulso se calcula como:\(y\left(s\right)=G(s)\); en el dominio del tiempo, la respuesta de impulso se da como:\(g(t)={\rm L}^{-1} \left[G(s)\right]\).

Para continuar, deje que la función de transferencia del sistema se represente en la forma factorizada como:

\[G\left(s\right)=\frac{n(s)}{\prod^n_{i=1}{\left(s-p_i\right)}}\]

donde\(n(s)\) es el polinomio numerador, y\(p_i,\ i=1,\dots n\), son los polos del sistema, se supone que son distintos y pueden incluir un solo polo en el origen. Usando expansión parcial de fracción (PFE), la respuesta de impulso se da como:

\[y_{imp}\left(s\right)=\sum^n_i{\frac{A_i}{s-p_i}}\]

Usando la transformada inversa de Laplace, la respuesta de impulso del sistema se calcula como:

\[y_{imp}\left(t\right)=\left(\sum^n_i{A_ie^{p_it}}\right)u(t)\]

donde\(u(t)\) representa la función unidad-paso, utilizada aquí para indicar que la expresión for\(g(t)\) es válida para\(t\ge 0\).

Respuesta al Impulso de los Sistemas de Orden Bajo

Sistema de primer orden

Dejar\(G(s)=\frac{1}{\tau s+1}\); el sistema tiene un modo de respuesta signle dado como:\(\{e^{-t/\tau }\}\). Así, la respuesta de impulso del sistema de primer orden se calcula como:\[g(t)=\frac{1}{\tau }e^{-t/\tau } u(t)\]

Ejemplo\(\PageIndex{1}\)

La respuesta impulsiva de\(G(s)=\frac{1}{s+1}\) se da como:\(g(t)=e^{-t}u(t)\).

La respuesta al impulso comienza\(g(0)=1\) y se acerca asintóticamente\(g(\infty)=0\).

pkg load control
s=tf('s');
Gs=1/(s+1);
impulse(Gs), grid on

Definición: Constante de tiempo del sistema

La constante de tiempo,\(\tau\), describe el tiempo en que, a partir de la unidad, la respuesta natural decae a\(e^{-1}\cong 0.37\), o 37% de su valor inicial. Para un sistema de primer orden, con un polo real,\(s=-\sigma\), la constante de tiempo se da como:\(\tau =\frac{1}{\sigma }\).

Sistema de segundo orden con un integrador

Dejar:\(G(s)=\frac{1}{s\left(\tau s+1\right)}\); entonces, los modos de respuesta naturales son:\(\left\{1,\ e^{-t/\tau }\right\}\). La función de transferencia se expande usando PFE como:\(G(s)=\frac{1}{s} +\frac{\tau }{\tau s+1}\). La respuesta al impulso se expresa como:\[g(t)=\left(1-e^{-t/\tau } \right)\, u(t)\]

Ejemplo\(\PageIndex{2}\)

La respuesta impulsiva de\(G(s)=\frac{1}{s(s+1)}=\frac{1}{s}-\frac{1}{s+1}\) se da como:\(g(t)=(1-e^{-t}) u(t)\).

La respuesta al impulso comienza\(g(0)=0\) y se acerca asintóticamente\(g(\infty)=1\).

pkg load control
s=tf('s');
Gs=1/s/(s+1);
impulse(Gs), grid on

Sistema de segundo orden con postes reales

Dejar\(G\left(s\right)=\frac{1}{\left(s+\sigma_1\right)\left(s+\sigma_2\right)}\); entonces, los modos de respuesta natural del sistema son:\(\left\{e^{-\sigma_1t},\ e^{-\sigma_2t}\right\}\). Suponiendo\(\sigma_2 \ge \sigma_1\), y usando PFE seguida de la transformada inversa de Laplace, la respuesta al impulso del sistema se expresa como:\[g(t)=\frac{1}{\sigma_2-\sigma_1}\left(e^{-\sigma_1t} -e^{-\sigma_2t} \right)\, u(t)\]

Ejemplo\(\PageIndex{3}\)

La respuesta impulsiva de\(G(s)=\frac{1}{(s+1)(s+2)}\) se da como:\(g(t)=(e^{-t}-e^{-2t}) u(t)\).

La respuesta al impulso comienza\(g(0)=0\) y se acerca asintóticamente\(g(\infty)=0\).

pkg load control
s=tf('s');
Gs=1/(s+1)/(s+2);
impulse(Gs), grid on

Sistema de segundo orden con polos complejos

Dejar\(G\left(s\right)=\frac{1}{{\left(s+\sigma \right)}^2+{\omega}^2}\); entonces, al usar la identidad de Euler, sus modos de respuesta naturales se dan como:\(\left\{e^{-\sigma t}{\cos \omega t\ },\ \ e^{-\sigma t}{\sin \omega t\ }\right\}\). Su respuesta impulsiva se da como:\[g(t)=\frac{1}{\omega } e^{-\sigma t} \; \sin (\omega t)\, u(t)\]

La respuesta natural oscilatoria está contenida en la envolvente definida por:\(\pm e^{-\sigma t}\). La constante de tiempo efectiva de un sistema de segundo orden se da como:\({\tau }_{eff}=\frac{1}{\sigma }\).

La respuesta natural es de la forma:\(y_n\left(t\right)=(C_1{\cos \omega t\ }+C_2{\sin \omega t\ })e^{-\sigma t}\) puede expresarse alternativamente como:\[y_n\left(t\right)=Ce^{-\sigma t}{sin \left(\omega t+\phi \right)\ }\] donde\(C=\sqrt{C^2_1+C^2_2}\) y\({tan \phi \ }=\frac{C_1}{C_2}\).

Ejemplo\(\PageIndex{4}\)

La respuesta al impulso de\(G(s)=\frac{s}{s^2+2s+2}=\frac{s}{(s+1)^2+1^2}=\frac{s+1-1}{(s+1)^2+1^2}\) se da como:\[g(t)=(\cos t-\sin t)e^{-t} u(t)=\sqrt{2}\sin (t+135^{\circ}) u(t)=\sqrt{2}\cos (t+45^{\circ})u(t)\]

La respuesta al impulso comienza\(g(0)=\cos(0)=1\) y se acerca asintóticamente\(g(\infty)=0\).

pkg load control
s=tf('s');
Gs=s/(s^2+2*s+2);
impulse(Gs), grid on

 

Figura\(\PageIndex{1}\): Respuesta de impulso de modelos de función de transferencia: (a) sistema de primer orden; (b) sistema de segundo orden con polo en origen; (c) sistema de segundo orden con polos reales; y, (d) sistema de segundo orden con polos complejos.

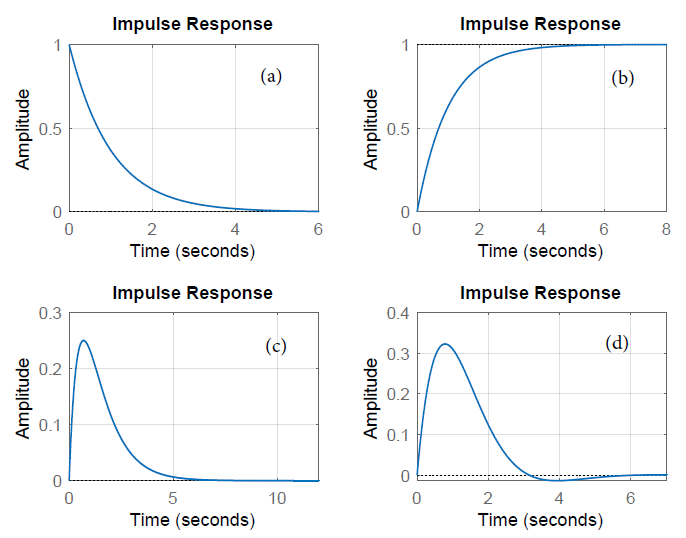
A partir de la figura, podemos observar que:

1. Mientras que la respuesta de impulso de un sistema de primer orden parte de un valor de unidad, la respuesta de impulso de un sistema de segundo orden parte de cero.
2. La respuesta al impulso de un sistema estable con polos en el plano abierto de la mitad izquierda (OLHP),\(Re\left(p_i\right)<0\), muere asintóticamente con el tiempo, es decir,\({\mathop{lim}_{t\to \infty } g\left(t\right)=0\ }\).
3. ; la respuesta al impulso de un sistema con un polo en el origen se acerca a un valor constante de unidad en el estado estacionario (que representa la integral de la función delta). Tales sistemas se califican marginalmente estables.