2.1: Polos y ceros del sistema

Polos y ceros del sistema

La función de transferencia,\(G(s)\), es una función racional en la variable de transformación de Laplace,\(s\). Se expresa como la relación entre el numerador y los polinomios denominador, es decir,\(G(s)=\frac{n(s)}{d(s)}\).

Definición: Ceros de función de transferencia

Las raíces del polinomio numerador,\(n(s)\), definen ceros del sistema, es decir, aquellas frecuencias a las que la respuesta del sistema es cero. Por lo tanto,\(z_0\) es un cero de la función de transferencia si\(G\left(z_0\right)=0.\)

Definición: Polos de función de transferencia

Las raíces del polinomio denominador,,\(d(s)\) definen los polos del sistema, es decir, aquellas frecuencias en las que la respuesta del sistema es infinita. Por lo tanto,\(p_0\) es un polo de la función de transferencia si\(G\left(p_0\right)=\infty .\)

A continuación se describen los polos y ceros de los modelos de sistema de primer y segundo orden.

Sistema de primer orden

Un sistema de primer orden tiene una descripción genérica de ODE:\(\tau \dot{y}\left(t\right)+y\left(t\right)=u(t)\), donde\(u\left(t\right)\) y\(y\left(t\right)\) denota la entrada y la salida, y\(\tau\) es la constante de tiempo del sistema. Al aplicar la transformada de Laplace, se obtiene una función de transferencia de primer orden como:\[G(s)=\frac{K}{\tau s+1}\]

La función de transferencia no tiene ceros finitos y un solo polo ubicado\(s=-\frac{1}{\tau }\) en el plano complejo.

Ejemplo\(\PageIndex{1}\)

El modelo de orden reducido de un motor de CC con entrada de voltaje y salida de velocidad angular (Ejemplo 1.4.3) se describe mediante la ecuación diferencial:\(\tau \dot\omega (t) + \omega(t) = V_a(t)\).

El motor de CC tiene una función de transferencia:\(G(s)=\frac{K}{\tau_m s+1}\) donde\(\tau_m\) esta la constante de tiempo del motor.

Para los siguientes valores de parámetros:\(R=1\Omega ,\; L=0.01H,\; J=0.01\; kgm^{2} ,\; b=0.1\; \frac{N-s}{rad} ,\; and\; k_{t} =k_{b} =0.05\), la función de transferencia del motor se evalúa como:

\[G(s)=\frac{\omega (s)}{V_{ a} (s)} =\frac{5}{s+10.25}=\frac{0.49}{0.098 s+1}\]

La función de transferencia tiene un solo polo ubicado en:\(s=-10.25\) con constante de tiempo asociada de\(0.098 sec\).

Sistema de segundo orden con un integrador

Un sistema de primer orden con un integrador se describe mediante la función de transferencia:

\[G\left(s\right)=\frac{K}{s(\tau s+1)}\]

El sistema no tiene ceros finitos y tiene dos polos ubicados en\(s=0\) y\(s=-\frac{1}{\tau }\) en el plano complejo.

Ejemplo\(\PageIndex{2}\)

El motor de CC modelado en el Ejemplo 2.1.1 anterior se utiliza en un sistema de control de posición donde el objetivo es mantener un cierto ángulo de eje\(\theta(t)\). La ecuación motora se da como:\(\tau \ddot\theta(t) + \dot\theta(t) = V_a(t)\); su función de transferencia se da como:\(G\left(s\right)=\frac{K}{s(\tau s+1)}\).

Usando los valores de parámetros anteriores en el modelo de motor de CC de orden reducido, la función de transferencia del sistema se da como:

\[G(s)=\frac{\theta (s)}{V_{ a} (s)} =\frac{5}{s(s+10.25)}=\frac{0.49}{s(0.098 s+1)}\]

La función de transferencia no tiene ceros finitos y los polos se encuentran en:\(s=0,-10.25\).

Sistema de segundo orden con postes reales

Un sistema de segundo orden con polos ubicados en\(s=-{\sigma }_1,\ -{\sigma }_2\) es descrito por la función de transferencia:

\[G\left(s\right)=\frac{1}{\left(s+{\sigma }_1\right)\left(s+{\sigma }_2\right)}\]

Ejemplo\(\PageIndex{3}\)

De la Sección 1.4, la función de transferencia del motor de CC se describe como:\[G(s)=\frac{K}{(s+1/\tau _{e} )(s+1/\tau _{m} )}\]

Entonces, los polos del sistema se ubican en:\(s_{1} =-\frac{1}{\tau _{m} }\)\(\tau_e\) y\(s_{2} =-\frac{1}{\tau _{e} }\), donde y\(\tau_{m}\) representan las constantes de tiempo eléctricas y mecánicas del motor.

Para los siguientes valores de parámetros:\(R=1\Omega ,\; L=0.01H,\; J=0.01\; kgm^{2} ,\; b=0.1\; \frac{N-s}{rad} ,\; and\; k_{t} =k_{b} =0.05\), la función de transferencia de voltaje de armadura a velocidad angular se da como:

\[\frac{\omega (s)}{V_{ a} (s)} =\frac{500}{(s+100)(s+10)+25} =\frac{500}{(s+10.28)(s+99.72)}\]

Los polos de función de transferencia se encuentran en:\(s=-10.28, -99.72\).

Las constantes de tiempo del motor se dan como:\(\tau _{e} \cong \frac{L}{R}=10 \;ms,\; \tau _ m \cong \frac{J}{b}=100\; ms\).

Sistema de segundo orden con polos complejos

Un modelo de segundo orden con sus polos complejos ubicados en:\(s=-\sigma \pm j\omega\) es descrito por la función de transferencia:

\[G\left(s\right)=\frac{K}{{\left(s+\sigma \right)}^2+{\omega }^2}.\]

Equivalentemente, la función de transferencia de segundo orden con polos complejos se expresa en términos de la relación de amortiguación\(\zeta\), y la frecuencia natural\({\omega }_n\), de los polos complejos como:

\[G(s)=\frac{K}{(s+\zeta {\omega }_n)^2+{\omega }^2_n(1-\zeta^2)}\]

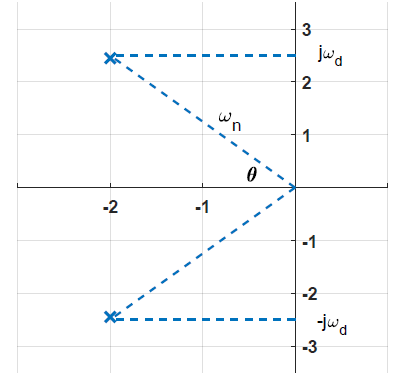
Los polos de función de transferencia se encuentran en:\(s_{1,2}=-\zeta {\omega }_n\pm j{\omega }_d\), donde\({\omega }_d=\omega_n\sqrt{1-{\zeta }^2}\) (Figura 2.1.1).

Como se ve en la figura,\({\omega }_n\) equivale a la magnitud del polo complejo, y\(\zeta =\frac{\sigma }{{\omega }_n}={\cos \theta }\), donde\(\theta\) está el ángulo subtendido por el polo complejo en el origen.

La relación de amortiguación\(\zeta\),, es una cantidad adimensional que caracteriza la decadencia de las oscilaciones en la respuesta natural del sistema. La relación de amortiguación se limita como:\(0<\zeta <1\).

1. Como\(\zeta \to 0\), los polos complejos se encuentran cerca del eje imaginario en:\(s\cong \pm j{\omega }_n\). La respuesta de impulso resultante muestra oscilaciones persistentes a la frecuencia natural del sistema,\({\omega }_n\).
2. Como\(\zeta \to 1\), los polos complejos se encuentran cerca del eje real como\(s_{1,2}\cong -\zeta {\omega }_n\). La respuesta de impulso resultante no tiene oscilaciones y decae exponencialmente a cero pareciéndose a la respuesta de un sistema de primer orden.

Ejemplo\(\PageIndex{4}\)

Un sistema de resorte-masa-amortiguador tiene una función de transferencia:

\[G(s)=\frac{1}{ms^{2} +bs+k}.\]

Su ecuación característica se da como:\(ms^s+bs+k=0\), cuyas raíces se caracterizan por el signo del discriminante,\(\Delta =b^{2} -4mk\).

Específicamente,

1. Para\(\Delta >0,\) el sistema cuenta con polos reales, ubicados en:

   \(s_{1,2} =-\frac{b}{2m} \pm \sqrt{\left(\frac{b}{2m} \right)^{2} -\frac{k}{m} }.\)

2. Para\(\Delta <0,\) el sistema cuenta con polos complejos, ubicados en:

   \(s_{1,2} =-\frac{b}{2m} \pm j\sqrt{\frac{k}{m} -\left(\frac{b}{2m} \right)^{2} }.\)

3. Para\(\Delta=0\), el sistema cuenta con dos polos reales e iguales, ubicados en:

   \(s_{1,2} =-\frac{b}{2m}.\)

A continuación, supongamos que la masa-resorte-amortiguador tiene los siguientes valores de parámetros:\(m=1, b=k=2\); entonces, su función de transferencia se da como:\[G(s)=\frac{1}{ms^2+bs+k}=\frac{1}{s^2+2s+2}\]

La función de transferencia tiene polos complejos ubicados en:\(s=-1\pm j1\).

Los polos complejos tienen:\({\omega }_n=\sqrt{2} \frac{rad}{s}, \zeta =\frac{1}{\sqrt{2}}\).

Además, los polos complejos tienen un ángulo:\(\theta=45^\circ\), y\(\cos45^\circ=\frac{1}{\sqrt{2}}\).

Figura\(\PageIndex{1}\): Ubicaciones de polos de función de transferencia de segundo orden en el plano complejo.