4.1: Estabilidad del Sistema de Circuito Cerrado

Estabilidad de bucle cerrado

Garantizar la estabilidad del circuito cerrado es el primer y principal objetivo de diseño del sistema de control. Aunque la planta física,\(G(s)\), puede ser estable, la presencia de retroalimentación puede hacer que el sistema de circuito cerrado se vuelva inestable, como en el caso de los modelos de planta de orden superior.

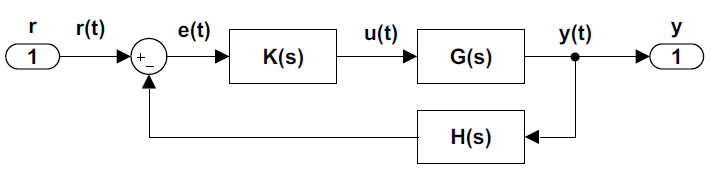
El diagrama de bloques estándar de un sistema de control de retroalimentación de entrada única y salida única (SISO) (Figura 4.1.1) incluye una planta\(G(s)\)\(K(s)\), un controlador y un sensor\(H(s)\), donde\(H\left(s\right)=1\) se asume.

Figura\(\PageIndex{1}\): Sistema de control de retroalimentación con planta\(G(s)\), sensor\(H(s)\), y controlador,\(K(s)\).

La función general de transferencia del sistema de entrada\(r(t)\),, a salida\(y(t)\), se da como:\[T(s)=\frac{KG(s)}{1+KGH(s)} \]

La determinación de la estabilidad se basa en el polinomio característico de bucle cerrado:\[\Delta (s,K)=1+KGH(s).\]

En particular, let\(G\left(s\right)=\frac{n\left(s\right)}{d\left(s\right)}\); then, asumiendo un controlador estático:\(K(s)=K\), el polinomio característico de bucle cerrado se da como:\[\Delta (s,K)=d(s)+Kn(s)\]

Alternativamente, suponiendo un controlador dinámico\(K\left(s\right)=\frac{n_C\left(s\right)}{d_C\left(s\right)}\), el polinomio característico se da como:\[\Delta (s)=d(s)d_{C} (s)+n(s)n_{C} (s)\]

Determinación de Estabilidad por Métodos Algebraicos

La estabilidad del polinomio característico está determinada por métodos algebraicos que caracterizan sus ubicaciones de raíz con base en los coeficientes del polinomio. A continuación, asumimos que\(\Delta (s)\) es un polinomio de orden\(n\) th expresado como:

\[\Delta (s)=s^{n} +a_{1} s^{n-1} +\ldots +a_{n-1} s+a_{n} \]

Condición Necesaria. Una condición necesaria para la estabilidad del polinomio es que los coeficientes\(a_i, \; i=1,2,\cdots,n\), sean todos distintos de cero y sean positivos, es decir,\(a_i>0\).

Condición Suficiente. Se obtiene una condición suficiente para la estabilidad polinómica mediante la aplicación de los siguientes criterios equivalentes:

El criterio de Hurwitz

El polinomio de orden\(n\) th,\(s^n+a_1s^{n-1}+\dots +a_n\) es estable, es decir, tiene sus raíces en el plano abierto de la mitad izquierda (OLHP), si y solo si los siguientes determinantes asumen valores positivos:

\[\left|a_{1} \right|,\; \; \left|\begin{array}{cc} {a_{1} } & {a_{3} } \\ {1} & {a_{2} } \end{array}\right|,\; \; \left|\begin{array}{ccc} {a_{1} } & {a_{3} } & {a_{5} } \\ {1} & {a_{2} } & {a_{4} } \\ {0} & {a_{1} } & {a_{3} } \end{array}\right|,\ldots\]

El criterio de Routh

El polinomio de orden\(n\) th,\(s^n+a_1s^{n-1}+\dots +a_n\) es estable, es decir, tiene sus raíces en el plano abierto de la mitad izquierda (OLHP), si y solo si todas las entradas en la matriz de Routh son positivas.

\[\begin{array}{c} {\begin{array}{c} {s^{n} } \\ {s^{n-1} } \\ {\vdots } \\ {} \\ {s^{1} } \\ {s^{0} } \end{array}} \end{array}\left|\begin{array}{c} {\begin{array}{cccc} {1} & {a_{2} } & {\ldots } & {} \\ {a_{1} } & {a_{3} } & {\ldots } & {} \\ {b_{1} } & {b_{2} } & {\ldots } & {} \\ {c_{1} } & {c_{2} } & {\ldots } & {} \\ {\ldots } & {} & {} & {} \\ {\ldots } & {} & {} & {} \end{array}} \end{array}\right.\]

Las dos primeras filas de la matriz de Routh se rellenan alternando los coeficientes del polinomio. Las entradas que aparecen en la tercera y subsiguientes filas se computan de la siguiente manera:

\(b_{1} =-\frac{1}{a_{1} } \left|\begin{array}{cc} {1} & {a_{3} } \\ {a_{1} } & {a_{2} } \end{array}\right|,\; \; b_{2} =-\frac{1}{a_{3} } \left|\begin{array}{cc} {a_{2} } & {a_{4} } \\ {a_{3} } & {a_{5} } \end{array}\right|,\; \; c_{1} =-\frac{1}{b_{1} } \left|\begin{array}{cc} {a_{1} } & {a_{3} } \\ {b_{1} } & {b_{2} } \end{array}\right|\), etc.

El criterio de estabilidad de Routh establece que el número de raíces inestables del polinomio es igual al número de cambios de signo en la primera columna de la matriz de Routh.

Determinación de estabilidad para polinomios de orden bajo

Los polinomios de orden bajo (es decir, polinomios de grado\(n=2,\; 3\)) a menudo se encuentran en el diseño de sistemas de control basados en modelos. El Routh o Hurwitz pueden simplificarse cuando se aplican a dichos polinomios.

Los criterios de estabilidad para polinomios de segundo y tercer orden se dan a continuación:

Polinomio de segundo orden: (\(n=2\)):\(\, a_{1} >0,\; \, a_{2} >0\).

Polinomio de tercer orden: (\(n=3\)):\(\, a_{1} >0,\quad a_{2} >0,\quad a_{3} >0,\quad a_{1} a_{2} -a_{3} >0.\)

Selección de ganancia del controlador

Las condiciones de estabilidad se pueden utilizar para determinar el rango de ganancia del controlador\(K\), para asegurar que las raíces del polinomio característico de bucle cerrado\(\Delta (s,K)\), se encuentran en el plano abierto de la mitad izquierda (OLHP).

Ejemplo\(\PageIndex{1}\)

Vamos\(G\left(s\right)=\frac{K}{s\left(s+2\right)}\),\(H\left(s\right)=1\); entonces,\(\Delta (s,K)=s^{2} +2s+K\). Mediante el uso de los criterios de estabilidad anteriores,\(\Delta (s)\) es estable para\(K>0\).

Ejemplo\(\PageIndex{2}\)

Vamos\(\Delta (s,K)=s^{3} +3s^{2} +2s+K\). Mediante el uso de los criterios de estabilidad anteriores,\(\; \Delta (s)\) es estable si se cumplen las siguientes condiciones:\(K>0\) y\(6-K>0\). En consecuencia, el rango de\(K\) para la estabilidad de bucle cerrado se da como\(0<K<6\).

Ejemplo\(\PageIndex{3}\)

El modelo simplificado de un pequeño motor de CC se da como:\(\frac{\theta (s)}{V_a (s)} =\frac{10}{s(s+6)} .\)

Un controlador PID para el modelo de motor se define como:\(K(s)=k_ p +k_ d s+\frac{k_ p }{s}\). El polinomio característico de bucle cerrado se da como:

\[\Delta (s)=s^{2} (s+6)+10(k_ d s^{2} +k_ p s+k_{i} )=s^{3} +(6+10k_ d )s^{2} +10k_ p s+10k_{i} .\]

Las restricciones en las ganancias del controlador PID para asegurar la estabilidad del polinomio de tercer orden se dan como:

\[k_ p ,\; k_{i} ,\; 6+10k_ d >0\]

\[k_ p (6+10k_ d )-k_{i} >0\]

Podemos elegir, por ejemplo,\(k_ p =1,\, k_ i =1,\, k_ d =1\) cumplir con los requisitos de estabilidad.

Determinación de Estabilidad a partir de Gráfica de Respuesta

La función de respuesta de frecuencia de la ganancia de bucle\(KGH\left(j\omega \right)\),, se puede utilizar para determinar la estabilidad del sistema de bucle cerrado. En particular, la condición raíz en el polinomio característico de bucle cerrado implica:\(1+KGH\left(j\omega \right)=0\), o\(KGH\left(j\omega \right)=-1\).

Por lo tanto, la estabilidad del sistema de bucle cerrado se puede inferir a partir de la respuesta de frecuencia de\(KGH\left(j\omega \right)\), relativa al\(1\angle \pm 180{}^\circ\) punto en el plano complejo. La determinación de estabilidad se realiza utilizando los siguientes criterios de estabilidad relativa:

Definición: Margen de ganancia

El margen de ganancia (GM) denota el factor por el cual la ganancia de bucle\(\ \left|KGH\left(j\omega \right)\right|\),, puede aumentarse sin comprometer la estabilidad de bucle cerrado.

El GM se calcula como:\(GM=-{\left|KGH\left(j{\omega }_{pc}\right)\right|}_{dB},\) donde\({\omega }_{pc}\) denota la frecuencia de cruce de fase definida por\(\angle KGH\left(j\omega \right)=-180{}^\circ\).

Un valor positivo de GM denota estabilidad de bucle cerrado.

Definición: Margen de fase

El margen de fase (PM) denota la fase adicional a la que el controlador puede agregar\(\angle KGH\left(j\omega \right)\) sin comprometer la estabilidad de bucle cerrado.

El PM se calcula como:\(PM=\angle KGH\left(j{\omega }_{gc}\right)+180{}^\circ ,\) donde\({\omega }_{gc}\) denota la frecuencia de cruce de ganancia definida por\({\left|KGH\left(j{\omega }_{gc}\right)\right|}_{dB}=0dB\).

Un valor positivo de PM denota estabilidad de bucle cerrado. Adicionalmente, PM representa una medida de estabilidad dinámica; por lo tanto, se desea PM adecuado para suprimir oscilaciones en la respuesta de salida.

Para continuar, supongamos que la función de transferencia de bucle\(KGH\left(s\right)\),, tiene\(m\) ceros y\(n\) polos. Entonces,

1. Para modelos de bajo orden (\(n\le 2)\), la ganancia de bucle\(KGH\left(s\right)\),, muestra un GM infinito.
2. GM es finito para\(n-m>2\) y puede ser así para\(n-m=2\).

El cruce de ganancia ocurre cuando\({\left|KGH\left(j0\right)\right|}_{dB}>0dB\); por lo tanto, PM se vuelve relevante solo en ese caso.

Determinación de Estabilidad en Gráfica de Bode

En la gráfica de magnitud Bode se indica la frecuencia de cruce de ganancia\({\omega }_{gc}\),, a medida que la gráfica de magnitud cruza la\(0dB\) línea. La gráfica de fase Bode a esa frecuencia revela el margen de fase como:\(PM=\angle KGH\left(j{\omega }_{gc}\right)+180{}^\circ\).

En la gráfica de fase Bode, la frecuencia de cruce de fase,\({\omega }_{pc}\), se indica a medida que la gráfica de fases cruza la\(-180{}^\circ\) línea. La gráfica de magnitud a esa frecuencia revela el margen de ganancia como:\(GM=-{\left|KGH\left(j{\omega }_{pc}\right)\right|}_{dB}\).

Los márgenes de estabilidad relativa se pueden obtener en MATLAB Control Systems Toolbox mediante el comando 'margin'. Cuando se invoca el comando produce una gráfica de Bode con márgenes de estabilidad indicados.

Ejemplo\(\PageIndex{1}\)

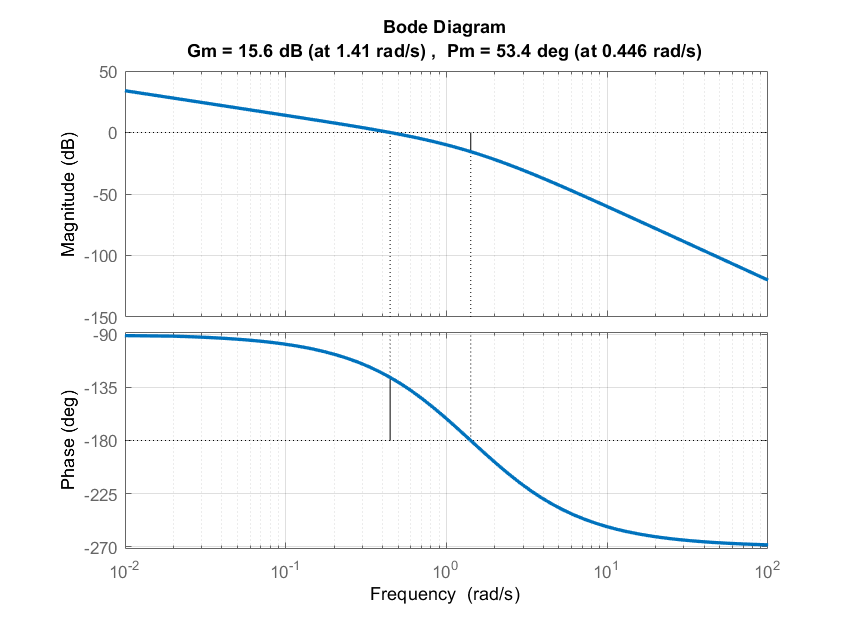
Let\(KG\left(s\right)=\frac{K}{s(s+1)(s+2)}\); las gráficas de magnitud y fase de Bode para\(K=1\) se muestran en la Figura 4.1.2.

La gráfica de magnitud Bode muestra un margen de\(15.6\;dB\) ganancia, es decir, la ganancia del controlador se puede aumentar por un factor de\(6\:(15.6\,dB)\) antes de perder la estabilidad del sistema de bucle cerrado.

La gráfica de fase Bode muestra un margen de\(53.4{}^\circ\) fase, lo que indica estabilidad de bucle cerrado; además, corresponde al\(\zeta \cong 0.55\) sistema de bucle cerrado, lo que indica una estabilidad dinámica adecuada.

Figura\(\PageIndex{2}\): Gráfica de ganancia y fase de Bode mostrando márgenes de estabilidad.

Determinación de Estabilidad en Gráfica Nyquist

En la gráfica de Nyquist, el cruce de ganancia se indica cuando la gráfica de Nyquist ingresa al círculo unitario, mientras que el cruce de fase se indica cuando la gráfica de Nyquist cruza el eje real negativo.

Por lo tanto, GM es positivo si el cruce del eje real está a la derecha del\(-1+j0\) punto. El PM es positivo si la\(KGH\left(j\omega \right)\) magnitud cae por debajo de la unidad en el tercer cuadrante.

Ejemplo\(\PageIndex{2}\)

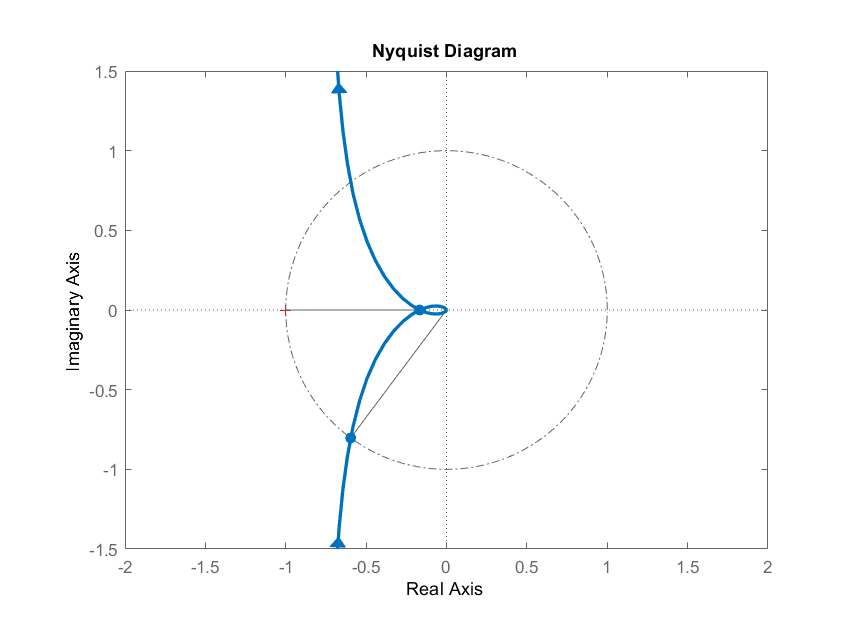
Let\(KG\left(s\right)=\frac{K}{s(s+1)(s+2)}\); la gráfica Nyquist para\(K=1\) se muestra en la Figura 4.1.3.

La trama Nyquist cruza el eje real en\(s=-0.165\), que corresponde a\(GM=6\).

La gráfica Nyquist ingresa al círculo unitario en un ángulo\(53^\circ\) desde el eje real negativo que indica el margen de fase.

Figura\(\PageIndex{3}\): Gráfica Nyquist que muestra márgenes de estabilidad.

 

Ejemplo\(\PageIndex{3}\)

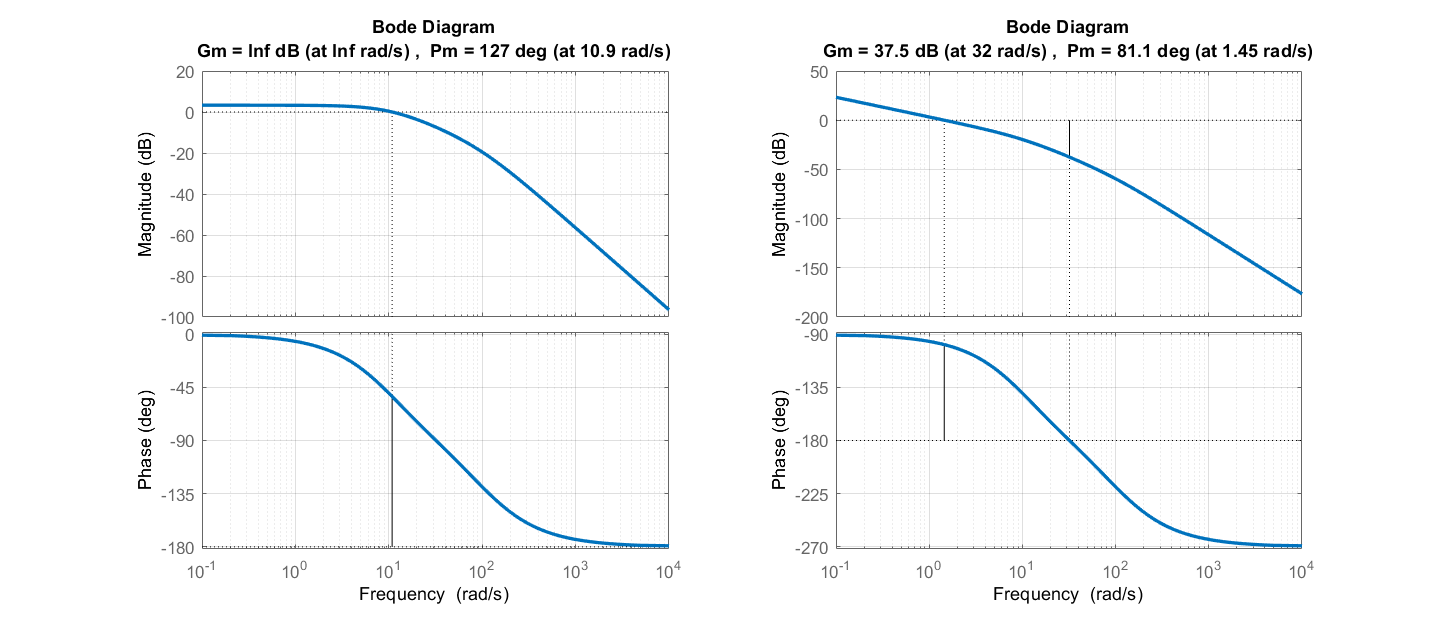
El modelo de un pequeño motor de CC, incluyendo un amplificador con una ganancia de 3 se da como:\(\frac{\omega (s)}{V_a (s)} =\frac{1500}{(s+100)(s+10)+25}\).

Los márgenes de estabilidad relativa para el modelo de motor de CC se dan como:\(GM=\infty ;PM=127{}^\circ\) (Figura 4.1.4).

Supongamos que el motor se utiliza en una aplicación de control de posición, de manera que la función de transferencia de planta se da como:\(\frac{\theta (s)}{V_a (s)} =\frac{1500}{s\left[(s+100)(s+10)+25\right]}\).

Los márgenes de estabilidad relativa correspondientes se dan como:\(GM=37.5\ dB;\ PM=81.1{}^\circ\) (Figura 4.1.4).

Figura\(\PageIndex{4}\): Márgenes de estabilidad para el modelo de motor de CC (izquierda); márgenes de estabilidad para la aplicación de control de posición (derecha).